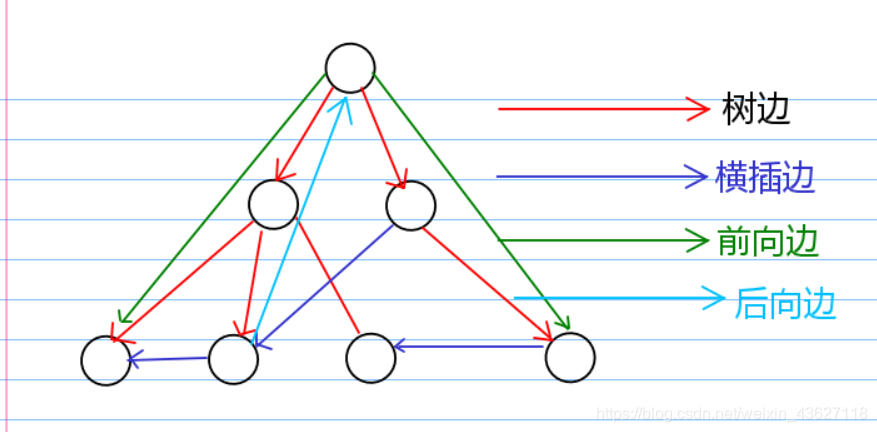
DAG的深度优先搜索标记

这是图论的基础知识点，也是学习Tarjan的导学课。

一、知识

对于在图G上进行深度优先搜索算法所产生的深度优先森林Gt，我们可以定义四种边的类型：

1.树边(Tree Edge)：为深度优先森林中Gt的边。如果结点v是因算法对边(u,v)的搜索而首先被发现，则(u,v)是一条树边。

2.后向边(Back Edge)：后向边(u,v)是将结点u连接到其在深度优先树中(一个)祖先结点v的边，由于有向图中可以有自循环，自循环也被认为是后向边。

3.前向边(Forward Edge)：是将结点u连接到其在深度优先树中一个后代结点v的边(u,v)。

4.横向边(Cross Edge)：指其他所有的边。这些边可以连接同一棵深度优先树中的结点，只要其中一个结点不是另外一个结点的祖先，也可以连接不同深度优先树中的两个结点。

附图：

二、方法

我们采取时间戳的思想：不会戳这里。

1.我们根据深度优先搜索的基本操作需要一个记录顶点相连的标志，也就是edge［］［］的一个二维数组， 然后，在遍历各个顶点的过程中将遇到的可以访问的edge设置为－1（初始化为0，输入时置为1）也就是已经访问过了， 至此，我们的树就会生成，但是我们需要记录其中不同边的特性，所以，我们增加两个标志位pre，post来记录开始和结束的时间点， 这个时间点起始点为0. 每当进行一次遍历则会将对应的时间点记录到相应顶点的pre和post中去，因此，我们可以有这样的想法： 1、需要判断一条边为back edge的话，只需要查看其相连顶点的post是否存在就可以了，因为从上到下的搜索过程中，只有该顶点结束搜索才会设置相应的结束时间 因而如果当前顶点的遍历都没有结束那么说明与该点相连的顶点形成的边是一条bakc edge。

2.从刚刚到back edge判断中我们可以联想发现，如果当前的顶点需要遍历且相连顶点的pre（开始时间）比当前顶点的pre高，说明这条边跳过一些时间点直接到此点 而且还是从较早到时间点跳转到较晚的时间点，因此这样的一条边是一条down edge。 3、可想而知如果一个顶点遍历的开始时间点远远大于另外一个顶点点话，这样形成的一条边自然就是cross edge了。

#include<iostream>
#include<queue>
#include<algorithm>
#include<set>
#include<cmath>
#include<vector>
#include<map>
#include<stack>
#include<bitset>
#include<cstdio>
#include<cstring>
//---------------------------------Sexy operation--------------------------//

#define cini(n) scanf("%d",&n)
#define cinl(n) scanf("%lld",&n)
#define cinc(n) scanf("%c",&n)
#define cins(s) scanf("%s",s)
#define coui(n) printf("%d",n)
#define couc(n) printf("%c",n)
#define coul(n) printf("%lld",n)
#define debug(n) printf("%d_________________________________\n",n);
#define speed ios_base::sync_with_stdio(0)
#define file  freopen("input.txt","r",stdin);freopen("output.txt","w",stdout)
//-------------------------------Actual option------------------------------//
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define Swap(a,b) a^=b^=a^=b
#define Max(a,b) (a>b?a:b)
#define Min(a,b) a<b?a:b
#define mem(n,x) memset(n,x,sizeof(n))
#define mp(a,b) make_pair(a,b)
#define pb(n)  push_back(n)
#define dis(a,b,c,d) ((double)sqrt((a-c)*(a-c)+(b-d)*(b-d)))
//--------------------------------constant----------------------------------//

#define INF  0x3f3f3f3f
#define esp  1e-9
#define PI   acos(-1)
using namespace std;
#define maxn 1020
#define INF 0x3f3f3f3f

using namespace std;
int pre[101],post[101],edge[101][101],parent[101];
int tag;
void dfs_tag(int cur,int n){
    pre[cur]=++tag;
    for(int i=0;i<n;i++){
        if(edge[cur][i]==1){
            if(pre[i]==0){
                parent[i]=cur;
                edge[cur][i]=-1;
                dfs_tag(i,n);
            }else{
                if(post[i]==0){edge[cur][i]=-2;}
                else if(pre[i]>pre[cur]){
                    edge[cur][i]=-3;
                }else{
                    edge[cur][i]=-4;
                }
                    }
        }
    }
    post[cur]=++tag;
}
void dfs(int n){
    memset(pre,0,sizeof(pre));
    memset(post,0,sizeof(post));
    memset(parent,-1,sizeof(parent));
    for (int i = 0; i < n; ++i)
    {
        if(parent[i]==-1)
            dfs_tag(i,n);
    }
}

int main(){
    int n,m;
    int u,v;
    int cases;
    tag=0;
    cin>>m>>n;
    for (int i = 0; i < m; ++i)
    {
        cin>>u>>v;
        edge[u][v]=1;
    }
    dfs(n);
    cin>>cases;
    while(cases--){
        cin>>u>>v;
        switch(edge[u][v]){
            case -1:
                printf("edge (%d,%d) is Tree Edge\n",u,v);
                break;
            case -2:
                printf("edge (%d,%d) is Back Edge\n",u,v);
                break;
            case -3:
                printf("edge (%d,%d) is Down Edge\n",u,v);
                break;
            case -4:
                printf("edge (%d,%d) is Cross Edge\n",u,v);
                break;
        }
    }
}