素数筛 : Eratosthenes 筛法, 线性筛法

这是两种简单的素数筛法, 好不容易理解了以后写篇博客加深下记忆

首先, 这两种算法用于解决的问题是 :

求小于n的所有素数 ( 个数 )

比如 这道题

在不了解这两个素数筛算法的同学, 可能会这么写一个isPrime, 然后遍历每一个数, 挨个判断 :

1. 从2判断到n-1

bool isPrime(int n) {
    for (int i = 2; i < n; i++)
        if (n % i == 0)
            return false;
    return true;
}

1. 从2判断到\(\sqrt{n}\)

bool isPrime(int n) {
    for (int i = 2; i <= sqrt(n); i++)
        if (n % i == 0)
            return false;
    return true;
}

然后再加上个count函数 :

int countPrimes2(int n) {
	int cnt = 0;
 	for(int i = 2; i < n; ++i) {
 		if(isPrime(i)) cnt++;
 	}
 	return  cnt;
}

这两种算法, 一个时间复杂度$ O(n^2) $ , 另一个 $ O(n \sqrt{n}) $ , 但凡出现这样类型的题, 这么写一般都超时了

下面介绍第一种算法

Eratosthenes 筛法 (厄拉多塞筛法)

核心思想 : 对于每一个素数, 它的倍数必定不是素数

我们通过直接标记, 可以大大减少操作量

比如从2开始遍历, 则4, 6, 8, 10, 12, 14....都不是素数,

然后是3, 则3, 6, 9, 12, 15.....都不是素数

如图更加直观 :

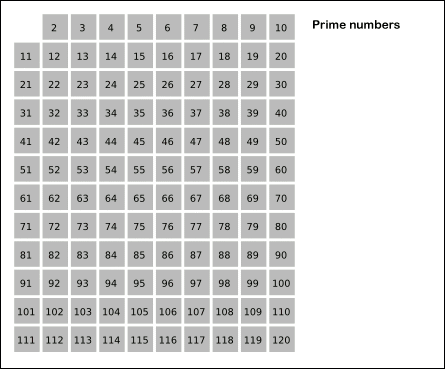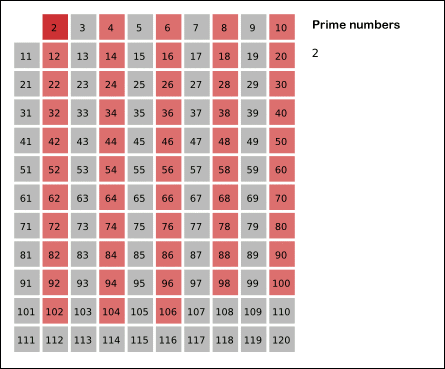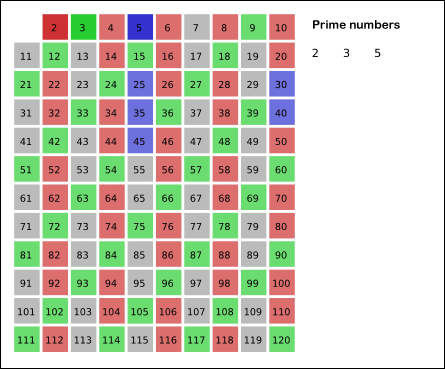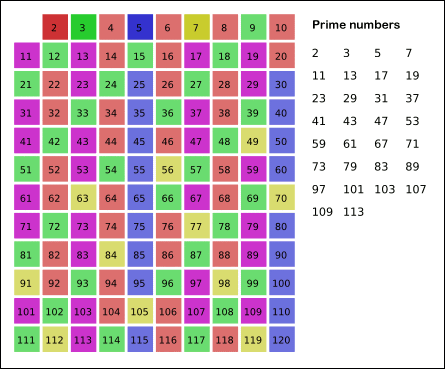
我们可以在判断小于等于数字n的时候增加一个vis数组, 他的大小等于n, 默认vis初始化为全零, 假设2-n都是素数, 接下来每遇到一个素数i, 把2-n中vis[i的倍数] = 1, 在接下来遇到的时候直接跳过就可以.

其时间复杂度为 : $ O(nloglogn) $

代码 :

 int countPrimes(int n) {
        vector<int> vis(n, 0); // all number : 0 means prime, 1 means not prime
        vector<int> prime(n, 0);
        int cnt = 0;
        for (int i = 2; i < n; ++i) {
            if (!vis[i]) {  // 如果vis[i]未被标记, 表明i是素数
                prime[++cnt] = i;
            	for (int j = i*2; j < n; j += i) {
                	vis[j] = 1; // 标记所有i的倍数
            	}
            }
        }
        return cnt;
    }

线性筛作为对Eratosthenes筛的改进, 能更大程度的减少时间复杂度:

O(n)的筛法----线性筛 ( 欧拉筛 )

在讲这个筛法之前, 明确一个概念 :

每一个合数 ( 除了1和它本身以外，还能被其他正整数整除 ), 都可以表示成n个素数的乘积

\[\boldsymbol{X}=\boldsymbol{p}_1\times \boldsymbol{p}_2\times \boldsymbol{p}_3\times \boldsymbol{p}_4\times ...\times \boldsymbol{p}_{\boldsymbol{i}}\,\,, \boldsymbol{X}为\text{合数}, \boldsymbol{p}为\text{素数}
\]

在Eratosthenes筛中, 我们可以发现, 在排除每一个质数的倍数时, 会有很多重复的操作 :

比如30 = 2x3x5, 那么30将在对2,3,5倍数标记的时候反复被处理3次

我们可以思考, 是否有一种方法, 可以仅仅将一个合数标记一次, 就可以打到筛选的目的呢 ?

可以设立一种规则 :

一个合数只能被他的最小素数因子筛去

比如30, 虽然他有2,3,5三个素因子, 我们只让在对2的倍数作标记时标记30

这样做, 可以保证我们对每一个数都仅仅只操作了一次, 时间复杂度也就变成了喜闻乐见的O(n) !

具体怎样实现 ?

我们在遍历2-n的过程中, 对每一个数i , 从当前已经找到的素数集中从2开始列出prime[j], 当什么时候有:

\[i\,\,\% \,prime\left[ j \right] ==\,\,0
\]

那么可以说明i含有prime[j]这个素因数, 也就是说, 对于比目前 i x prime[j]更大的数, prime[j]将不再是它的最小素因数, 因此到此这一轮筛可以停止了.

举个例子 :

当 i = 9 时 :

我们可以筛出 :

9 x 2 = 18 ---- 然后进行判断 9%2 != 0, 因此继续筛

9 x 3 = 27 ---- 然后进行判断 9%3 ==0, 因此break

假设我们继续筛 9 x 5, 会发生什么?

由于9 % 3 == 0了, 则可以知道 9含有3这个素因数, 如果继续筛9x5, 可以知道5并不是9x5的最小素因数, 因此不应当在这一轮被筛去.

代码 :

int countPrimes(int n) {
        vector<int> vis(n, 0);  // all number : 0 means prime, 1 means not prime
        vector<int> prime(n, 0);
        int cnt = 0;
        for (int i = 2; i < n; ++i) {
            if (!vis[i])
                prime[cnt++] = i;
            for(int j = 0; j < cnt && i * prime[j] < n; ++j)
            {
                vis[i*prime[j]] = 1;
                if (i % prime[j] == 0)  // if prime[j] is i*prime[j]'s minimum prime
                    break;
            }
        }
        return cnt;
    }

时间比较

写了个cpp计时, 来比较一下这几种算法的时间吧~

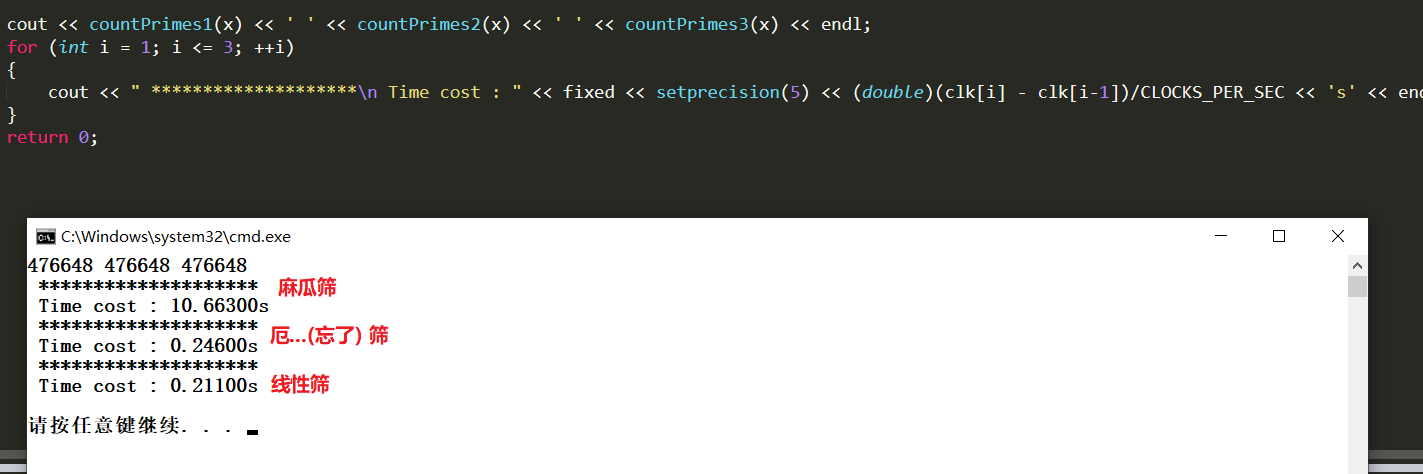
可以看到, Eratosthenes和线性筛的时间稍有区别, 加大数据量会放大这个区别, 但是麻瓜筛\(O(n^2)\) 在n=7000000的时候已经10s+了, 再加大数据量估计得等到明天了

在写题的这段日子, 每天都在看别人代码的卧槽声中度过

---

ref :

OI - wiki 筛法 : https://oi-wiki.org/math/sieve/

线性筛法求素数的原理与实现 : https://wenku.baidu.com/view/4881881daaea998fcc220e99.html

leetcode题解 : https://leetcode-cn.com/problems/count-primes/solution/