数值计算方法实验之Hermite 多项式插值 (Python 代码)

一、实验目的

在已知f(x),x∈[a,b]的表达式，但函数值不便计算,或不知f(x),x∈[a,b]而又需要给出其在[a,b]上的值时，按插值原则f(x_i)= y_i(i= 0,1…….,n)求出简单函数P(x)(常是多项式),使其在插值基点x_i,处成立P(x_i)= y_i(i=0,1,……,n),而在[a,b]上的其它点处成立f(x)≈P(x).

二、实验原理

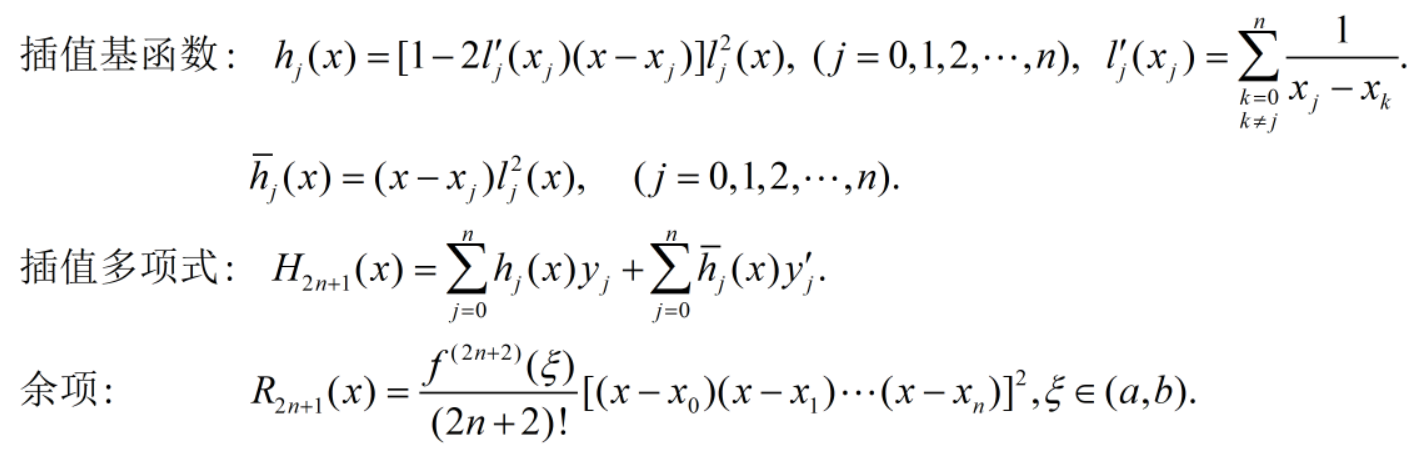
三、实验内容

求f(x)=x⁴在[0,2]上按5个等距节点确定的Hermite插值多项式.

四、实验程序

 import numpy as np
 from sympy import *
 import matplotlib.pyplot as plt

 def f(x):
     return  x ** 4

 def ff(x):  # f[x0, x1, ..., xk]
     ans = 0
     for i in range(len(x)):
         temp = 1
         for j in range(len(x)):
             if i != j:
                 temp *= (x[i] - x[j])
         ans += f(x[i]) / temp
     return ans

 def draw(L, newlabel= 'Lagrange插值函数'):
     plt.rcParams['font.sans-serif'] = ['SimHei']
     plt.rcParams['axes.unicode_minus'] = False
     x = np.linspace(0, 2, 100)
     y = f(x)
     Ly = []
     for xx in x:
         Ly.append(L.subs(n, xx))
     plt.plot(x, y, label='原函数')
     plt.plot(x, Ly, label=newlabel)
     plt.xlabel('x')
     plt.ylabel('y')
     plt.legend()

     plt.savefig('1.png')
     plt.show()

 def lossCal(L):
     x = np.linspace(0, 2, 101)
     y = f(x)
     Ly = []
     for xx in x:
         Ly.append(L.subs(n, xx))
     Ly = np.array(Ly)
     temp = Ly - y
     temp = abs(temp)
     print(temp.mean())

 def calM(P, x):
     Y =   n ** 4
     dfP = diff(P, n)
     return solve(Y.subs(n, x[0]) - dfP.subs(n, x[0]), [m,])[0]

 if __name__ == '__main__':
     x = np.array(range(11)) - 5
     y = f(x)

     n, m = symbols('n m')
     init_printing(use_unicode=True)

     P = f(x[0])
     for i in range(len(x)):
         if i != len(x) - 1:
             temp = ff(x[0:i + 2])
         else:
             temp = m
         for j in x[0:i + 1]:
             temp *= (n - j)
         P += temp
     P = expand(P)

     P = P.subs(m, calM(P, x))
     draw(P, newlabel='Hermite插值多项式')
     lossCal(P)

五、运算结果