Java实现 LeetCode 688 “马”在棋盘上的概率（DFS+记忆化搜索）

688. “马”在棋盘上的概率

已知一个 NxN 的国际象棋棋盘，棋盘的行号和列号都是从 0 开始。即最左上角的格子记为 (0, 0)，最右下角的记为 (N-1, N-1)。

现有一个 “马”（也译作 “骑士”）位于 (r, c) ，并打算进行 K 次移动。

如下图所示，国际象棋的 “马” 每一步先沿水平或垂直方向移动 2 个格子，然后向与之相垂直的方向再移动 1 个格子，共有 8 个可选的位置。

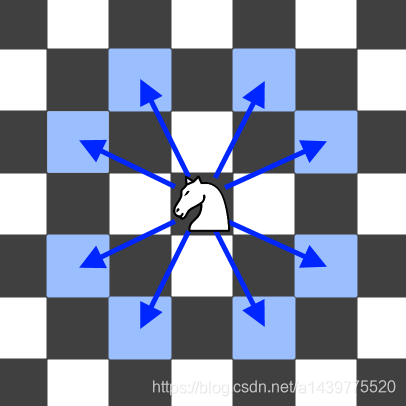
现在 “马” 每一步都从可选的位置（包括棋盘外部的）中独立随机地选择一个进行移动，直到移动了 K 次或跳到了棋盘外面。

求移动结束后，“马” 仍留在棋盘上的概率。

示例：

输入: 3, 2, 0, 0

输出: 0.0625

解释:

输入的数据依次为 N, K, r, c

第 1 步时，有且只有 2 种走法令 “马” 可以留在棋盘上（跳到（1,2）或（2,1））。对于以上的两种情况，各自在第2步均有且只有2种走法令 “马” 仍然留在棋盘上。

所以 “马” 在结束后仍在棋盘上的概率为 0.0625。

注意：

N 的取值范围为 [1, 25]

K 的取值范围为 [0, 100]

开始时，“马” 总是位于棋盘上

class Solution {
    int[][] move = { { 1, 2 }, { 1, -2 }, { 2, 1 }, { 2, -1 }, { -1, 2 }, { -1, -2 }, { -2, 1 }, { -2, -1 } };
	double[][][] dp;

	public double knightProbability(int N, int K, int r, int c) {
		dp = new double[N][N][K + 1];
		if (K == 0)
			return 1;
		return dfs(N, K, r, c);
	}

	private double dfs(int N, int K, int r, int c) {
		if (dp[r][c][K] != 0)
			return dp[r][c][K];
		double res = 0;
		for (int i = 0; i < 8; i++) {
			int r1 = r + move[i][0];
			int c1 = c + move[i][1];
			if (r1 >= 0 && r1 < N && c1 >= 0 && c1 < N) {
				res += (K == 1 ? 1 : dfs(N, K - 1, r1, c1));
			}
		}
		return dp[r][c][K] = res / 8;
	}
}