C++实现车轮轨迹

标题：车轮轴迹

栋栋每天骑自行车回家需要经过一条狭长的林荫道。道路由于年久失修，变得非常不平整。虽然栋栋每次都很颠簸，但他仍把骑车经过林荫道当成一种乐趣。

由于颠簸，栋栋骑车回家的路径是一条上下起伏的曲线，栋栋想知道，他回家的这条曲线的长度究竟是多长呢？更准确的，栋栋想知道从林荫道的起点到林荫道的终点，他的车前轮的轴（圆心）经过的路径的长度。

栋栋对路面进行了测量。他把道路简化成一条条长短不等的直线段，这些直线段首尾相连，且位于同一平面内。并在该平面内建立了一个直角坐标系，把所有线段的端点坐标都计算好。

假设栋栋的自行车在行进的过程中前轮一直是贴着路面前进的。

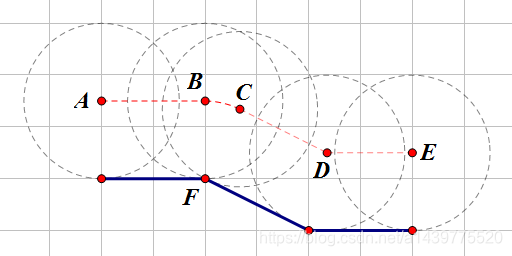
图1给出了一个简单的路面的例子，其中蓝色实线为路面，红色虚线为车轮轴经过的路径。在这个例子中，栋栋的前轮轴从A点出发，水平走到B点，然后绕着地面的F点到C点（绕出一个圆弧），再沿直线下坡到D点，最后水平走到E点，在这个图中地面的坐标依次为：(0, 0), (2, 0), (4, -1), (6, -1)，前轮半径为1.50，前轮轴前进的距离依次为：

AB=2.0000；弧长BC=0.6955；CD=1.8820；DE=1.6459。

总长度为6.2233。

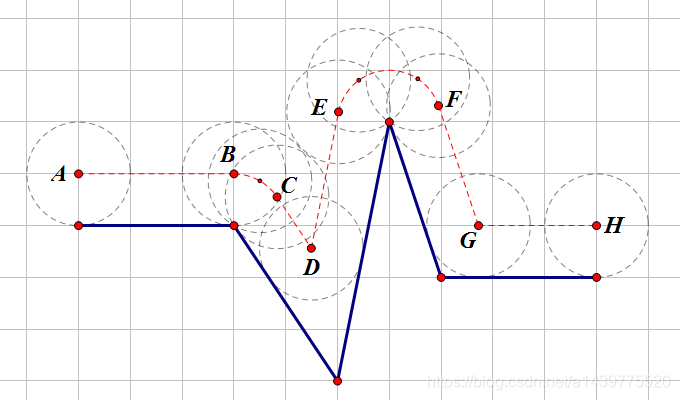
图2给出了一个较为复杂的路面的例子，在这个例子中，车轮在第一个下坡还没下完时（D点）就开始上坡了，之后在坡的顶点要从E绕一个较大的圆弧到F点。这个图中前轮的半径为1，每一段的长度依次为：

AB=3.0000；弧长BC=0.9828；CD=1.1913；DE=2.6848；弧长EF=2.6224； FG=2.4415；GH=2.2792。

总长度为15.2021。

现在给出了车轮的半径和路面的描述，请求出车轮轴轨迹的总长度。

输入的第一行包含一个整数n和一个实数r，用一个空格分隔，表示描述路面的坐标点数和车轮的半径。

接下来n行，每个包含两个实数，其中第i行的两个实数x[i], y[i]表示描述路面的第i个点的坐标。

路面定义为所有路面坐标点顺次连接起来的折线。给定的路面的一定满足以下性质：

*第一个坐标点一定是(0, 0)；

*第一个点和第二个点的纵坐标相同；

*倒数第一个点和倒数第二个点的纵坐标相同；

*第一个点和第二个点的距离不少于车轮半径；

*倒数第一个点和倒数第二个点的的距离不少于车轮半径；

*后一个坐标点的横坐标大于前一个坐标点的横坐标，即对于所有的i，x[i+1]>x[i]。

输出一个实数，四舍五入保留两个小数，表示车轮轴经过的总长度。

你的结果必须和参考答案一模一样才能得分。数据保证答案精确值的小数点后第三位不是4或5。

【样例输入1】

4 1.50

0.00 0.00

2.00 0.00

4.00 -1.00

6.00 -1.00

【样例输出1】

6.22

【样例说明1】

这个样例对应图1。

【样例输入2】

6 1.00

0.00 0.00

3.00 0.00

5.00 -3.00

6.00 2.00

7.00 -1.00

10.00 -1.00

【样例输出2】

15.20

【样例说明2】

这个样例对应图2

【数据规模与约定】

对于20%的数据，n=4；

对于40%的数据，n≤10；

对于100%的数据，4≤n≤100，0.5≤r≤20.0，x[i] ≤2000.0，-2000.0≤y[i] ≤2000.0。

资源约定：

峰值内存消耗 < 64M

CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0

注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。

注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型(千万不要混淆c和cpp)。

锦囊

有20%的数据n=4，此时路面由两段水平线和一个坡组成，可以分为上坡和下坡讨论，可以推导出数学公式，这20%的分数比较好拿。

此题正确的做法是：对于每个条线段，将这条线段按车轮的半径平移到路面上方，然后在每个线段的端点画一个圆。由这些平移后的线段和圆组成的最上面的一条线就是车轮的路径，接下来需要算出这条线。

这条线是一条分段连续的线，每段或者是一条直线段，或者是一段圆弧。先求出所有直线段与直线段、直线段与圆、圆与圆的交点，并把所有的端点，所有圆的左右边界一起放入一个集合中，这个集合中的所有横坐标就是可能分段的坐标。按这个集合的坐标分段，每一段分别计算。每一段只需要找到最靠上方的线段/弧即可，最终将所有段的线段和弧的长度相加得到答案。

本题与几何关系较大，公式推导是一个麻烦之处。另外选手可能漏考虑一些情况而失分。本题对编程的要求较高，较容易写错，而且不好调试。

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cmath>
#include <algorithm>

using namespace std;

const int MAXN = 10000;
const double PI = atan(1.0) * 4;
const double EPS = 1e-10;

class Point {
public:
	double x, y;
	Point() {}
	Point(double x, double y) : x(x), y(y) {}
	Point operator - (const Point &r) const { return Point(x-r.x, y-r.y); }
	Point operator + (const Point &r) const { return Point(x+r.x, y+r.y); }
	Point &operator += (const Point &r) { x += r.x; y += r.y; return *this; }
	Point &operator *= (double m) { x *= m; y *= m; return *this; }
	Point pOfRotate(double angle) const {
		double cosA = cos(angle);
		double sinA = sin(angle);
		return Point(cosA*x-sinA*y, sinA*x+cosA*y);
	}
	Point pOfRotate90() const { return Point(-y, x); }
	double length() const { return sqrt(x*x+y*y); }
	Point pOfNormal() const {
		double len = length();
		return Point(x/len, y/len);
	}
	double angle() const { return atan2(y, x); }
};

ostream & operator <<(ostream &os, const Point &v)
{
	os << "(" << v.x << "," << v.y << ")";
	return os;
}

class Segment;
class Circle;

class Seg {
public:
	virtual double getLeft() const = 0;
	virtual double getRight() const = 0;
	virtual double getY(double x) const = 0;
	virtual double getLength(double x1, double x2) const = 0;
	virtual void intersect(Seg *r) const = 0;
	virtual void intersect(const Segment &v) const = 0;
	virtual void intersect(const Circle &v) const = 0;
	bool contains(double x) const { return x>=getLeft() && x<=getRight(); }
	virtual void acceptPrint(ostream &os) const = 0;
};

ostream & operator <<(ostream &os, const Seg &v)
{
	v.acceptPrint(os);
	return os;
}

Point intersectRet[4];
int tIntersectRet;

class Segment : public Seg {
public:
	Point a, b;
	Segment &moveLeft(double dis)
	{
		Point tmp = ((b-a).pOfRotate90().pOfNormal() *= dis);
		a += tmp;
		b += tmp;
		return *this;
	}
	virtual double getLeft() const { return a.x; }
	virtual double getRight() const { return b.x; }
	virtual double getY(double x) const {
		return (x-a.x)*(b.y-a.y)/(b.x-a.x)+a.y;
	}
	virtual double getLength(double x1, double x2) const {
		return (x2-x1) * (b-a).length() / (b.x-a.x);
	}
	virtual void intersect(Seg *r) const {
		r->intersect(*this);
	}
	virtual void intersect(const Segment &v) const {
		tIntersectRet = 0;
		double ang = (b-a).angle();
		Point c = (v.a-a).pOfRotate(-ang);
		Point d = (v.b-a).pOfRotate(-ang);
		// Bug
		//double di = b.length();
		double di = (b-a).length();
		if (!((c.y>0&&d.y<0) || (c.y<0&&d.y>0)))
			return ;
		double x = (d.x-c.x) * (-c.y) / (d.y-c.y) + c.x;
		if (x<0 || x>di)
			return ;
		Point ret = Point(x,0).pOfRotate(ang)+a;
		intersectRet[tIntersectRet++] = ret;
	}
	virtual void intersect(const Circle &v) const;
	virtual void acceptPrint(ostream &os) const {
		os << a << "-" << b;
	}
};

class Circle : public Seg {
public:
	Point c;
	double r;
	virtual double getLeft() const { return c.x - r; }
	virtual double getRight() const { return c.x + r; }
	virtual double getY(double x) const {
		double y2 = r * r - (c.x - x) * (c.x - x);
		if (y2<0) y2 = 0;
		return c.y + sqrt(y2);
	}
	virtual double getLength(double x1, double x2) const {
		x1 -= c.x; x2 -= c.x;
		double a1 = Point(x1, sqrt(abs(r*r-x1*x1))).angle(), a2 = Point(x2, sqrt(abs(r*r-x2*x2))).angle();
		return (a1-a2) * r;
	}
	virtual void intersect(Seg *r) const {
		r->intersect(*this);
	}
	virtual void intersect(const Segment &v) const {
		tIntersectRet = 0;
		Point a = v.a - c;
		Point b = v.b - c;
		double ang = (b-a).angle();
		Point nA = a.pOfRotate(-ang);
		Point nB = b.pOfRotate(-ang);
		double y = nA.y;
		if (y>r || y<-r)
			return ;
		double x = sqrt(r*r - y*y);
		if (x>=nA.x && x<=nB.x)
			intersectRet[tIntersectRet++] = Point(x, y).pOfRotate(ang) + c;
		if (-x>=nA.x && -x<=nB.x)
			intersectRet[tIntersectRet++] = Point(-x, y).pOfRotate(ang) + c;
	}
	virtual void intersect(const Circle &v) const {
		tIntersectRet = 0;
		Point p = v.c - c;
		double d = p.length();
		if (d > r + v.r || d==0)
			return ;
		double x = (r*r - v.r*v.r + d*d) / (2*d);
		if (x <= r)
		{
			double y = sqrt(abs(r*r - x*x));
			double ang = p.angle();
			intersectRet[tIntersectRet++] = Point(x,y).pOfRotate(ang) + c;
			intersectRet[tIntersectRet++] = Point(x,-y).pOfRotate(ang) + c;
		}
	}
	virtual void acceptPrint(ostream &os) const {
		os << c << "," << r;
	}
};

void Segment::intersect(const Circle &v) const {
	v.intersect(*this);
}

int n;
Point inps[MAXN];
vector<Seg *> segs;
vector<double> spes;
double radius = 1;

void input()
{
	scanf("%d%lf", &n, &radius);
	for (int i = 0; i < n; ++i)
	{
		double x, y;
		scanf("%lf%lf", &x, &y);
		inps[i] = Point(x, y);
	}
}

void process()
{
	segs.clear();
	spes.clear();
	for (int i = 1; i + 1 < n; ++i)
	{
		Circle *tmp = new Circle;
		tmp->c = inps[i];
		tmp->r = radius;
		segs.push_back(tmp);
	}
	for (int i = 0; i + 1 < n; ++i)
	{
		Segment *tmp = new Segment;
		tmp->a = inps[i];
		tmp->b = inps[i+1];
		tmp->moveLeft(radius);
		segs.push_back(tmp);
	}
	for (int i = 0; i < (int)segs.size(); ++i)
	{
		spes.push_back(segs[i]->getLeft());
		spes.push_back(segs[i]->getRight());
	}
	for (int i = 0; i < (int)segs.size(); ++i)
	{
		for (int j = i+1; j < (int)segs.size(); ++j)
		{
			segs[i]->intersect(segs[j]);
			if (tIntersectRet > 0)
			{
				for (int id = 0; id < tIntersectRet; ++id)
				{
					//cout << *segs[i] << " " << *segs[j] << " : " << intersectRet[id] << endl;
					spes.push_back(intersectRet[id].x);
				}
			}
		}
	}
	sort(spes.begin(), spes.end());
	double pre = spes[0];
	const double NONE = 1e30;
	double preEnd = NONE;
	double totalLen = 0;
	for (int i = 1; i < (int)spes.size(); ++i)
	{
		if (spes[i]-pre < EPS)
			continue;
		double cur = (pre+spes[i]) / 2;
		//cout << "Processing " << cur << "  from " << pre << " to " << spes[i] << endl;
		if (cur>=inps[0].x && cur<=inps[n-1].x)
		{
			double MY = -NONE;
			int who;
			for (int j = 0; j < (int)segs.size(); ++j)
			{
				if (!segs[j]->contains(cur))
					continue;
				double y = segs[j]->getY(cur);
				if (y > MY)
				{
					MY = y;
					who = j;
				}
			}
			if (preEnd != NONE)
			{
				double LY = segs[who]->getY(pre);
				//cout << "Drop info " << *segs[who] << " " << "[" << pre << "]" << endl;
				totalLen += abs(preEnd-LY);
				//cout << "Pre drop = " << abs(preEnd-LY) << "  from " << preEnd << " to " << LY << endl;
			}
			double len = segs[who]->getLength(pre, spes[i]);
			if (len < 0)
				printf("Error!\n");
			//cout << "Curlen = " << len << " from " << pre << " to " << spes[i] << endl;
			totalLen += len;
			preEnd = segs[who]->getY(spes[i]);
		}
		pre = spes[i];
	}
	printf("%0.2lf\n", totalLen);
	for (int i = 0; i < (int)segs.size(); ++i)
		delete segs[i];
	segs.clear();
}

int main()
{
	input();
	process();
	return 0;
}