confidence intervals and precision|The One-Mean z-Interval Procedure|When to Use the One-Mean z-Interval Procedure

Confidence Intervals for One Population Mean When σ Is Known

Obtaining Confidence Intervals for a Population Mean When σ Is Known

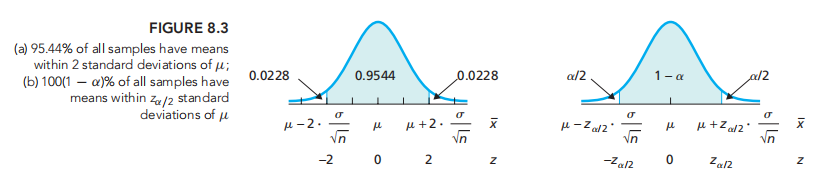
The z-interval procedure works reasonably well even when the variable is not normally distributed and the sample size is small or moderate, provided the variable is not too far from being normally distributed. Thus we say that the z-interval procedure is robust to moderate violations of the normality assumption.‡

样本情况与z-interval之间的关系与使用，这需要使用之前综合sample情况进行考虑：

对于偏斜分布的sample：需要取更大的size

†Statisticians also consider skewness. Roughly speaking, the more skewed the distribution of the variable under consideration, the larger is the sample size required for the validity of the z-interval procedure

可以使用不同的描述方法，发现此sample是一个偏斜分布：

.

置信区间的本质：

The length of the confidence interval indicates the precision of the estimate, or how well we have “pinned down” μ. Long confidence intervals indicate poor precision; short confidence intervals indicategood precision.

如图：比较两种不同置信区间：

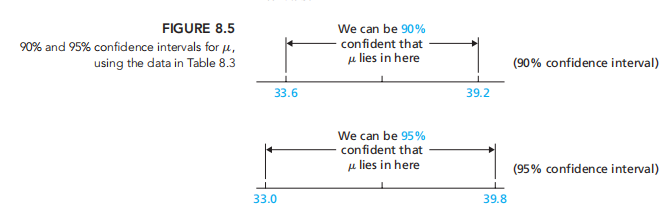
所以：