s曲线

一。 原型

sigmoid 函数原型：

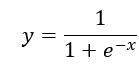
在 [-5, 5] 上的曲线是这个样子的：

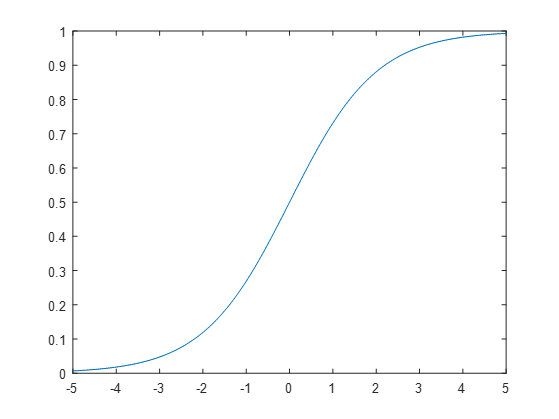
二。X轴变形

如果我们希望加速更快一点，那么就需要对原型中的指数 -X 的系数进行改变。原型可以认为是 -(1 * X)，如果我们需要把图形Y不变，X压缩为原来的 1 /5，那么只需要指数改为 -(5 * X)，这样图形就更加陡峭。此处指数部分变形为 -aX。原始图形是 [-5, 5] 这个区间，一共是10个数字，压缩后的整个区间为 [- t / 2, t / 2]，那么 a = 10 / t。

我们注意到，原型中X轴的坐标是 从负数到正数，那么我们需要的图形X坐标是从 0 开始的，所以需要对压缩后的图形进行平移，平移的 X 行程为 t / 2。所以指数变形为 - (10 / t) * (X - t / 2), 展开为 -( 5 * 2 / t ) * X + 5 的 -ax + b 的形式，其中 a = 5 * 2 / t, b = 5。因为原始图形对应的区间是 [-5, 5]，如果我们设 F = 5，那么在区间 [- F, F ] 上的 s 曲线进行 x 方向的压缩平移后 指数部分变为 -( F * 2 / t ) * X + F .

整体的公式为 y = 1 / ( 1 + e ^ ( - ( F * 2 / t ) * X + F ) )

y = \frac{1}{1 + e ^ {- (F * \frac{2}{t}) * x + F}}

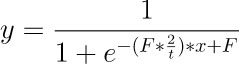
三。Y轴变形

原始图形的 Y 轴区间是 [0, 1]，实际使用中我们需要在 Y 轴进行拉伸，所以需要增加系数 Ymax - 0，我们有时候还需要图形Y轴不从0开始，需要一个最小的 Y 轴偏移 Ymin，所以 Y轴拉伸的系数变为 Ymax - Ymin。

整体公式变为 y = (ymax - ymin)( 1 / ( 1 + e ^ ( - ( F * 2 / t ) * X + F ) ) ) + ymin

y = (y_{max} - y_{min}) * \frac{1}{1 + e ^ {- (F * \frac{2}{t}) * x + F}} + y_{min}

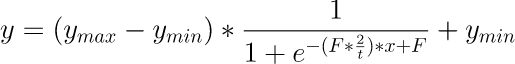
注： 使用 在线公式 https://latex.vimsky.com/