RocksDB事务的隔离性分析【原创】

Rocksdb事务隔离性指的是多线程并发事务使用时候，事务与事务之间的隔离性，通过加锁机制来实现，本文重点剖析Read Commited隔离级别下，Rocksdb的加锁机制。

1. Rocksdb事务相关类族

Rocksdb的事务相关的类图如下图所示。主要有两个类族，Transaction和DB，默认采用PessimisticTransaction，而PessimisticTransaction内部的加锁机制通过TransactionLockMgr来实现的。

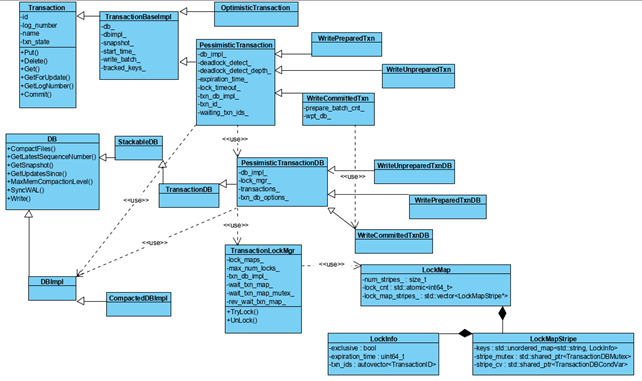
TransactionLockMgr内部维护了LockMap。TransactionLockMgr根据每个记录的Key计算hash值，再对num_stripes取模，在LockMap中的向量Std::vector<LockMapStripe>定位LockMapStripe，这样减少实体锁的竞争激烈程度，相当于锁分解。

LockMap的数据成员如下

Size_t num_stripes          LockMapStripe个数，默认16个

Std::vector<LockMapStripe>   LockMapStripe数组

LockMapStripe的数据成员如下

std::shared_ptr<TransactionDBMutex>  stripe_mutex :   实体锁

std::shared_ptr<TransactionDBCondVar>  stripe_cv :     实体条件变量

std::unordered_map<std::string, LockInfo>  keys :       具有相同Key hash值的每条记录的加锁信息，std::string为记录的Key值。

LockInfo的数据成员如下

bool exclusive :                     排它锁，还是共享锁

uint64_t expiration_time :            锁的过期时间

autovector<TransactionID>  txn_ids :   这把锁阻塞的事务ID列表

2. Rocksdb事务流程分析

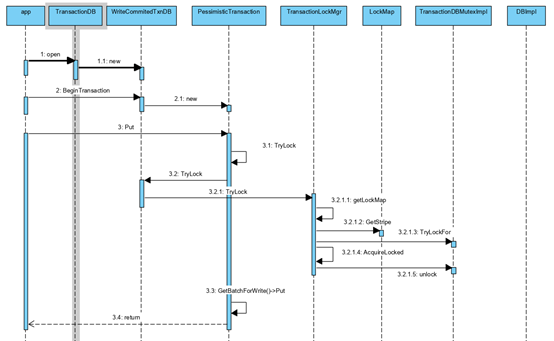
上述流程，是应用创建TransactionDB，然后Put一条记录，再Commit的协作流程图，在Put阶段调用TransactionLockMgr的TryLock方法，Commit阶段调用TransactionLockMgr的UnLock方法。

TransactionLockMgr：：TryLock内部的主要逻辑在AcquireLocked函数中，TransactionLockMgr：：UnLock内部的主要逻辑在UnlockKey函数中，下面具体分析这两个函数。绿色部分字体为个人注解。

AcquireLocked

Status TransactionLockMgr::AcquireLocked(LockMap* lock_map,

LockMapStripe* stripe,

const std::string& key,    //记录的Key值

Env* env,

LockInfo&& txn_lock_info,  //当前事务锁信息

uint64_t* expire_time,     //锁的过期时间

autovector<TransactionID>* txn_ids)

{

Status result;

auto stripe_iter = stripe->keys.find(key);  // 检查这条记录的Key是否已经被加锁了。

if (stripe_iter != stripe->keys.end()) {       // 这条记录的Key已经被之前事务加过锁

LockInfo& lock_info = stripe_iter->second;

if (lock_info.exclusive || txn_lock_info.exclusive) {   //之前事务或者当前事务加的是排他锁，

if (lock_info.txn_ids.size() == 1 &&

lock_info.txn_ids[0] == txn_lock_info.txn_ids[0]) {  //之前加锁的事务就是当前事务

lock_info.exclusive = txn_lock_info.exclusive;

lock_info.expiration_time = txn_lock_info.expiration_time;

} else {       //之前加锁的事务不是当前事务

if (IsLockExpired(txn_lock_info.txn_ids[0], lock_info, env,

expire_time)) {   // 之前事务加的锁已经过期，可以清除

lock_info.txn_ids = txn_lock_info.txn_ids;

lock_info.exclusive = txn_lock_info.exclusive;

lock_info.expiration_time = txn_lock_info.expiration_time;

} else {

result = Status::TimedOut(Status::SubCode::kLockTimeout);

*txn_ids = lock_info.txn_ids;   // 返回之前事务列表

}

}

} else {   //当前事务加的是共享锁

lock_info.txn_ids.push_back(txn_lock_info.txn_ids[0]);

lock_info.expiration_time =

std::max(lock_info.expiration_time, txn_lock_info.expiration_time);

}

} else {  // 这条记录的Key没有被之前事务加过锁

if (max_num_locks_ > 0 &&

lock_map->lock_cnt.load(std::memory_order_acquire) >= max_num_locks_) {

result = Status::Busy(Status::SubCode::kLockLimit);

} else {

// 当前事务执行加锁操作

stripe->keys.emplace(key, std::move(txn_lock_info));

if (max_num_locks_) {

lock_map->lock_cnt++;

}

}

}

return result;

}

UnlockKey逻辑相对简单一些，主要是删除加锁的记录，并且唤醒被阻塞的事务。

void TransactionLockMgr::UnLockKey(const PessimisticTransaction* txn,

const std::string& key,

LockMapStripe* stripe, LockMap* lock_map,

Env* env) {

TransactionID txn_id = txn->GetID();

auto stripe_iter = stripe->keys.find(key);

if (stripe_iter != stripe->keys.end()) {

auto& txns = stripe_iter->second.txn_ids;

auto txn_it = std::find(txns.begin(), txns.end(), txn_id);

// Found the key we locked.  unlock it.

if (txn_it != txns.end()) {

if (txns.size() == 1) {

stripe->keys.erase(stripe_iter);

} else {

auto last_it = txns.end() - 1;

if (txn_it != last_it) {

*txn_it = *last_it;

}

txns.pop_back();

}

if (max_num_locks_ > 0) {

// Maintain lock count if there is a limit on the number of locks.

assert(lock_map->lock_cnt.load(std::memory_order_relaxed) > 0);

lock_map->lock_cnt--;

}

}

} else {

// This key is either not locked or locked by someone else.  This should

// only happen if the unlocking transaction has expired.

assert(txn->GetExpirationTime() > 0 &&

txn->GetExpirationTime() < env->NowMicros());

}

}