matplotlib 强化学习

matplotlib 强化学习

import matplotlib.pyplot as plt
...![](https://img2020.cnblogs.com/blog/1642028/202006/1642028-20200621111043462-144482637.png)

plt.show()		#显示图像；下面都要写，就不重复了

二维图表

1. 基本图表

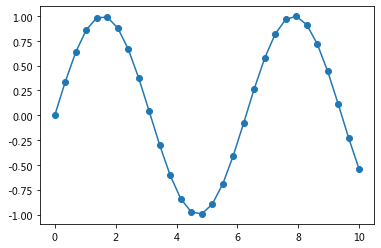
1. 用plot方法画出x=(0,10)间sin的图像

x = np.linspace(0, 10, 30)  #产生0-10之间的30个均匀数组
plt.plot(x, np.sin(x));		#以x为横坐标，sin(x)为纵坐标打印出图像

注：

• linspace生成的是包含结尾的数组，比如0-10生成11个数才是0,1,2,3,4,5...
• 生成10个数则是0，1.11111111, 2.22222222, 3.33333333, 4.44444444...；
• 而arrange是不包含结尾的，0-10生成10个数是0,1,2,3...

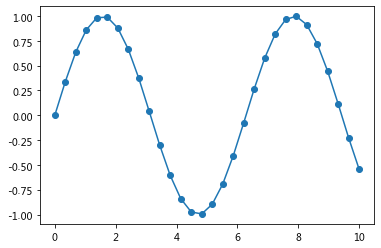
1. 用点,线的方式画出x=(0,10)间sin的图像

plt.plot(x, np.sin(x), '-o');
#'o’代表每个数据点用小圆圈表示，且数据点之前不用线连接，看起来很像散点图
#'ro'代表小圆圈是红色的
#'-'就是最普通的线型，数据点之间用实线连接。
#'--'设置线性为虚线

!

1. 用scatter方法画出x=(0,10)间sin的点图像

plt.scatter(x, np.sin(x));		#散点图

1. 用饼图的面积及颜色展示一组4维数据

rng = np.random.RandomState(0)
x = rng.randn(100)			#生成随机数组
y = rng.randn(100)
colors = rng.rand(100)
sizes = 1000 * rng.rand(100)

plt.scatter(x, y, c=colors, s=sizes, alpha=0.3,
cmap='viridis')
plt.colorbar(); 			# 展示色阶

绘制柱状图

x = [1,2,3,4,5,6,7,8]
y = [3,1,4,5,8,9,7,2]
label=['A','B','C','D','E','F','G','H']

plt.bar(x,y,tick_label = label);	#纵向升高
plt.barh(x,y,tick_label = label);	#换成横向

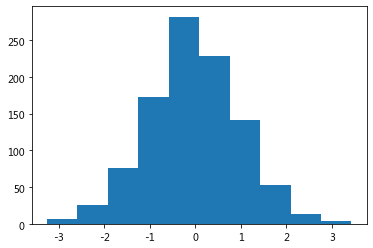
直方图

data = np.random.randn(1000) #生成1000个随机数
plt.hist(data);				#画出图像

!

2. 自定义图表元素

x = np.linspace(0,10,100)
plt.plot(x, np.sin(x))
plt.ylim(-1.5, 1.5);		#设置y轴显示范围为(-1.5,1.5)

x = np.linspace(0.05, 10, 100)
y = np.sin(x)
plt.plot(x, y, label='sin(x)')
plt.xlabel('variable x');			#设置x,y轴标签variable x，value y
plt.ylabel('value y');
plt.title('三角函数');					#设置图表标题“三角函数”
plt.text(3.2, 0, 'sin(x)', weight='bold', color='r');	#注释

plt.annotate('maximum',xy=(np.pi/2, 1),xytext=(np.pi/2+1, 1),weight='bold',color='r',arrowprops=dict(arrowstyle='->', connectionstyle='arc3', color='r'));					#箭头标识

显示网格

x = np.linspace(0.05, 10, 100)
y = np.sin(x)
plt.plot(x, y)
plt.grid()

...
参数
matplotlin.pyplot.grid(b, which, axis, color, linestyle, linewidth， **kwargs) axis : 取值为‘both’， ‘x’，‘y’。就是想绘制哪个方向的网格线。不过我在输入参数的时候发现如果输入x或y的时候，             输入的是哪条轴，则会隐藏哪条轴

color : 这就不用多说了，就是设置网格线的颜色。或者直接用c来代替color也可以。
plt.grid(c='g') 设置颜色为绿色

linestyle :也可以用ls来代替linestyle， 设置网格线的风格，是连续实线，虚线或者其它不同的线条。 | '-' | '--' | '-.' | ':' | 'None' | ' ' | '']
plt.grid(linestyle='-.')

linewidth : 设置网格线的宽度
...

绘制平行于x轴y=0.8的水平参考线

x = np.linspace(0.05, 10, 100)
y = np.sin(x)
plt.plot(x, y)
plt.axhline(y=0.8, ls='--', c='r')#水平参考线

3. 自定义图像

在一张图里绘制sin,cos的图形，并展示图例

x = np.linspace(0, 10, 1000)
fig, ax = plt.subplots()

ax.plot(x, np.sin(x), label='sin')
ax.plot(x, np.cos(x), '--', label='cos')
ax.legend();

多子图

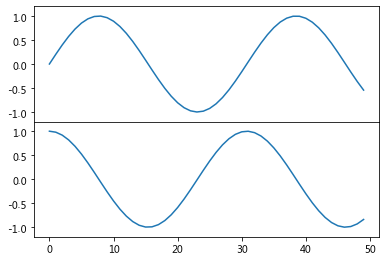
在2个子图中，显示sin(x)和cos(x)的图像

fig = plt.figure()
ax1 = fig.add_axes([0.1, 0.5, 0.8, 0.4], ylim=(-1.2, 1.2))
ax2 = fig.add_axes([0.1, 0.1, 0.8, 0.4], ylim=(-1.2, 1.2))

x = np.linspace(0, 10)
ax1.plot(np.sin(x));
ax2.plot(np.cos(x));

for i in range(1, 7):		#用for创建6个子图，并且在图中标识出对应的子图坐标
plt.subplot(2, 3, i)
plt.text(0.5, 0.5, str((2, 3, i)),fontsize=18, ha='center')

组合绘制大小不同的子图

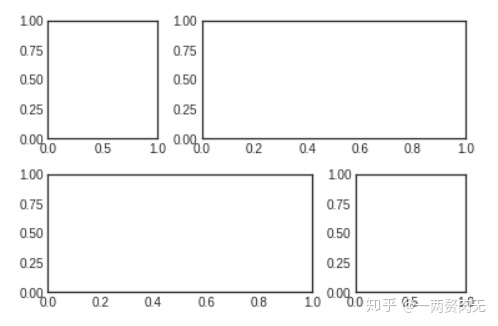
grid = plt.GridSpec(2, 3, wspace=0.4, hspace=0.3)
plt.subplot(grid[0, 0])
plt.subplot(grid[0, 1:])
plt.subplot(grid[1, :2])
plt.subplot(grid[1, 2]);

三维图像

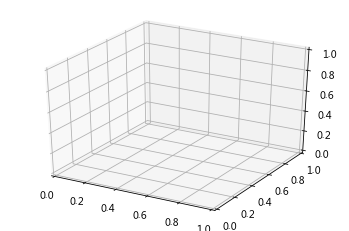
#38.创建一个三维画布
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes(projection='3d')

#39.绘制一个三维螺旋线
ax = plt.axes(projection='3d')
# Data for a three-dimensional line
zline = np.linspace(0, 15, 1000)
xline = np.sin(zline)
yline = np.cos(zline)
ax.plot3D(xline, yline, zline);

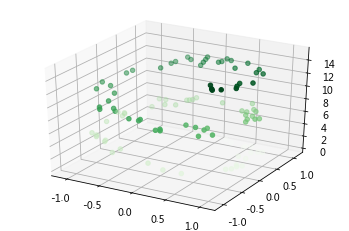
#40.绘制一组三维点
ax = plt.axes(projection='3d')
zdata = 15 * np.random.random(100)
xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens');

import numpy  as np
from matplotlib import pyplot  as plt
from mpl_toolkits.mplot3d import Axes3D
q1 = np.arange(0.01, 1, 0.01)
q2 = np.arange(0.01, 1 , 0.01)  #生成一位基底
q1, q2 = np.meshgrid(q1, q2)    #混合成二维数组，形成二维基底

pCDa = (1-q1)
pCDb = (np.sqrt((1-q1)**2+q1**2)-q1)
s_pCD = -q1* np.log2(q1) - (1-q1) * np.log2(1-q1)
Q_MID1 = s_pCD *q2 /q2        #AB或CD的关联值，下图是(s_x_pCD - s_pCD) *q2；  *q2/q2后才是圆柱体

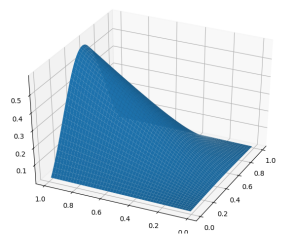
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(q1,q2,Q_MID1)     #表面图
ax.set_xlabel('value of q2')
ax.set_ylabel('value of q1')
ax.set_zlabel('the value of Q_MID1(pCD)')
plt.show()

#参数
ax.plot_surface(X, Y, Z, *args, **kwargs)
X,Y,Z：数据
rstride、cstride、rcount、ccount:同Wireframe plots定义
color:表面颜色
cmap:图层

参考文献：

1. https://www.kesci.com/home/project/5de9f0a0953ca8002c95d2a9 50题matplotlib从入门到精通

2. https://www.cnblogs.com/knightoffz/p/12933716.html 大创项目经历

3. https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html 官方文档

4. https://www.cnblogs.com/xingshansi/p/6777945.html 参考博客