【分类器】感知机+线性回归+逻辑斯蒂回归+softmax回归

一、感知机

    详细参考：https://blog.csdn.net/wodeai1235/article/details/54755735

1.模型和图像：

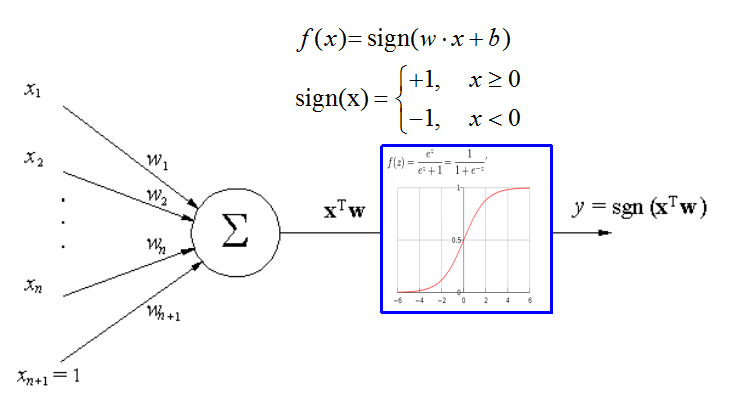
2.数学定义推导和优化：

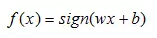
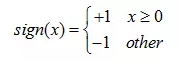
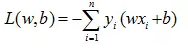
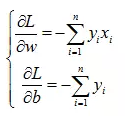
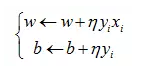
3.流程

二、线性回归

     1.定义及解析解：

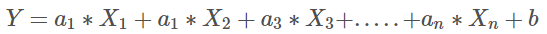
a=(X^TX) ^-1 X^Ty，如加2范数约束则解析解为a=(X^TX+λI) ^-1 X^Ty

    2.总结：

速度快，对异常值敏感。可以采用梯度下降法。

三、逻辑斯蒂回归

1.sigmod：

见 https://www.cnblogs.com/EstherLjy/p/9343487.html

2.概述：

LR是一种二分类算法，直接对分类的可能性进行建模，无需事先假设数据分布，避免了假设不准确带来的问题。不仅能预测出类别，还能预测出该类别的概率。是一种针对线性可分问题的性能优异的模型。LR回归是在线性回归模型的基础上，使用sigmoid函数，将线性模型 w^Tx的结果压缩到[0,1] 之间，使其拥有概率意义。

3.推导：

α=sigmod(α) 是预测值，y是gt

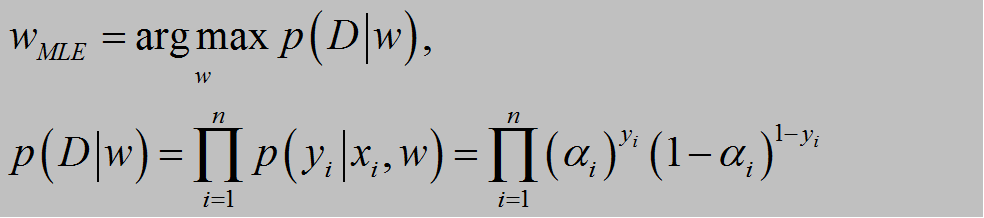
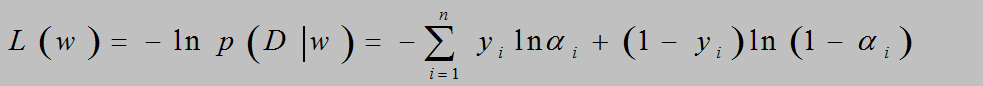
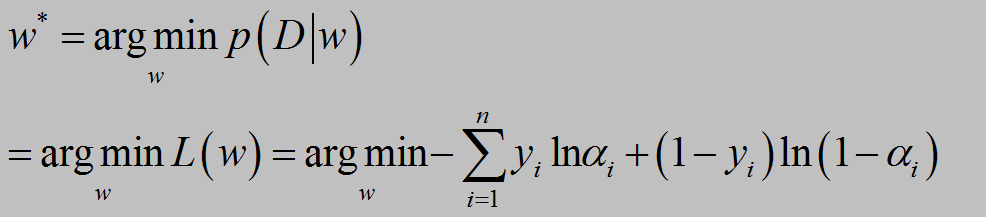
L(w)的导数为∑(yi-αi)xi

然后用梯度下降法求解。

4.逻辑斯蒂回归和线性分类器对比

y的取值范围不同，线性是正负无穷，逻辑斯蒂是0-1;

逻辑斯蒂更符合实际，一般x很大或很小时对y影响不大，中间影响很大。

线性回归是根据样本X各个维度的Xi的线性叠加得到预测值的Y，然后最小化所有的样本预测值Y与真实值y'的误差来求得模型参数，是线性的。在logistic回归中，X各维度叠加和与Y不是线性关系，而是logistic关系。

四、softmax回归

1.概述：

是对LR在多分类上的一种扩展，损失函数为：

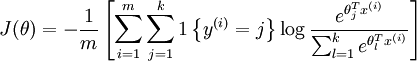
LR的损失为：

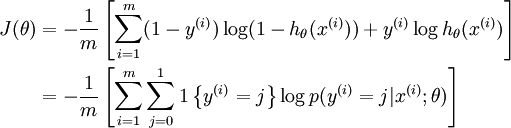
2.适用情况：

   softmax与LR的one VS all并不完全相同，区别在于加起来是否等于1.

使用softmax:k个类是互斥的。

使用n个二分类的LR：k个类不互斥。

3.参考：

https://blog.csdn.net/zhangliyao22/article/details/48379291

https://www.cnblogs.com/lianyingteng/p/7784158.html