图->连通性->有向图的强连通分量

文字描述

　　有向图强连通分量的定义：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

　　用深度优先搜索求有向图的强连通分量的方法如下并假设有向图的存储结构为十字链表。

　　1 在有向图G上，从某个定点出发沿以该顶点为尾的弧进行深度优先遍历；并按其所有邻接点的搜索都完成(即退出DFS函数)的顺序将顶点排列起来。此时需对之前的深度优先遍历算法(见图遍历)作两处修改: (a)在进入DSFTraverse函数时首先进行计数变量的初始化，即在入口处加上count=0;(b)在退出DFS函数之前将完成搜索的顶点号记录在另一个辅助数组finished[vexnum]中，即在DFS函数结束之前加上finished[count++]=v；

　　2 在有向图G上，从最后完成搜索的顶点(即finished[count-1])出发，沿着以该顶点为头的弧作逆向的深度优先搜索遍历，若遍历不能访问到有向图中所有顶点，则从余下的顶点中最后完搜索的那个顶点出发，继续作逆向的深度优先搜索便利。依次类推。

　　由此，每一次调用DFS作逆向深度优先遍历所访问到的顶点集便是有向图G中一个强连通分量的顶点集。

示意图

见本章后面的代码运行Example01, Example02, Example03, Example04。

算法分析

求有向图的强连通分量的算法时间复杂度和深度优先搜索遍历相同。

代码实现

 

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>
 #define    MAX_VERTEX_NUM    20
 #define    DEBUG
 #ifdef DEBUG
 #include <stdarg.h>
 #define LOG(args...) _log_(__FILE__, __FUNCTION__, __LINE__, ##args);
 void _log_(const char *file, const char *function, int line, const char * format, ...)
 {
     char buf[] = {};
     va_list list;
     va_start(list, format);
     sprintf(buf, "[%s,%s,%d]", file, function, line);
     vsprintf(buf+strlen(buf), format, list);
     sprintf(buf+strlen(buf), "\n");
     va_end(list);
     printf(buf);
 }
 #else
 #define LOG
 #endif // DEBUG

 //////////////////////////////////////////////////////////////
 // 十字链表作为图的存储结构
 //////////////////////////////////////////////////////////////
 typedef enum {DG, DN, UDG, UDN} GraphKind;
 typedef char InfoType;
 typedef char VertexType;
 typedef struct ArcBox{
     int tailvex, headvex;
     struct ArcBox *hlink, *tlink;
     InfoType *info;
 }ArcBox;
 typedef struct VexNode{
     VertexType data;
     ArcBox *firstin, *firstout;
 }VexNode;
 typedef struct{
     VexNode xlist[MAX_VERTEX_NUM];
     int vexnum, arcnum;
     GraphKind kind;
 }OLGraph;

 //////////////////////////////////////////////////////////////
 // 若G中存在顶点u，则返回该顶点在图中位置；否则返回-1。
 //////////////////////////////////////////////////////////////
 int LocateVex(OLGraph G, VertexType v)
 {
     int i = ;
     for(i=; i<G.vexnum; i++)
     {
         if(G.xlist[i].data == v)
             return i;
     }
     return -;
 }

 //////////////////////////////////////////////////////////////
 // 若G中存在顶点位置loc存在,则返回其顶点名称
 //////////////////////////////////////////////////////////////
 VertexType LocateVInfo(OLGraph G, int loc)
 {
     return G.xlist[loc].data;
 }

 //////////////////////////////////////////////////////////////
 // 以十字链表作为图的存储结构创建有向图
 //////////////////////////////////////////////////////////////
 int CreateDG(OLGraph *G)
 {
     printf("\n以十字链表作为图的存储结构创建有向图:\n");
     int i = , j = , k = , IncInfo = ;
     int v1 = , v2 = ;
     char tmp[] = {};
     ArcBox *p = NULL;
     printf("输入顶点数，弧数，其他信息标志位: ");
     scanf("%d,%d,%d", &G->vexnum, &G->arcnum, &IncInfo);
     for(i=; i<G->vexnum; i++)
     {
         //输入顶点值
         printf("输入第%d个顶点: ", i+);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         //初始化指针
         G->xlist[i].data = tmp[];
         G->xlist[i].firstin = NULL;
         G->xlist[i].firstout = NULL;
     }
     //输入各弧并构造十字链表
     for(k=; k<G->arcnum; k++)
     {
         printf("输入第%d条弧(顶点1, 顶点2): ", k+);
         memset(tmp, , sizeof(tmp));
         scanf("%s", tmp);
         sscanf(tmp, "%c,%c", &v1, &v2);
         i = LocateVex(*G, v1);
         j = LocateVex(*G, v2);
         //对弧结点赋值
         p = (ArcBox *) malloc(sizeof(ArcBox));
         p->tailvex = i;
         p->headvex = j;
         p->hlink = G->xlist[j].firstin;
         p->tlink = G->xlist[i].firstout;
         p->info = NULL;
         //完成在入弧和出弧链头的插入
         G->xlist[j].firstin = p;
         G->xlist[i].firstout = p;
         //若弧有相关的信息,则输入
         if(IncInfo)
         {
             //Input(p->info);
         }
     }
     return ;
 }

 int CreateGraph(OLGraph *G)
 {
     printf("输入图类型: +有向图(0), -有向网(1), -无向图(2), -无向网(3): ");
     scanf("%d", &G->kind);
     switch(G->kind){
         case DG:
             return CreateDG(G);
         case DN:
         case UDN:
         case UDG:
         default:
             printf("not support!\n");
             return -;
     }
     return ;
 }

 //////////////////////////////////////////////////////////////
 // 打印图结点
 //////////////////////////////////////////////////////////////
 void printG(OLGraph G)
 {
     printf("\n打印图结点\n");
     if(G.kind == DG){
         printf("类型：有向图；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == DN){
         printf("类型：有向网；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == UDG){
         printf("类型：无向图；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }else if(G.kind == UDN){
         printf("类型：无向网；顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum);
     }
     int i = ;
     ArcBox *fi = NULL;
     ArcBox *fo = NULL;
     for(i=; i<G.vexnum; i++)
     {
         printf("%c: ", G.xlist[i].data);
         fi = G.xlist[i].firstin;
         fo = G.xlist[i].firstout;
         printf("{hlink=");
         while(fi)
         {
             printf("(%d,%c)->(%d,%c); ", fi->tailvex, LocateVInfo(G, fi->tailvex), fi->headvex, LocateVInfo(G, fi->headvex));
             fi = fi->hlink;
         }
         printf("}        {tlink=");
         while(fo)
         {
             printf("(%d,%c)->(%d,%c); ", fo->tailvex, LocateVInfo(G, fo->tailvex), fo->headvex, LocateVInfo(G, fo->headvex));
             fo = fo->tlink;
         }
         printf("}\n");
     }
     return ;
 }

 //////////////////////////////////////////////////////////////
 // 用双向遍历的方法求有向图的强连通分量
 //////////////////////////////////////////////////////////////
 int GVisited[MAX_VERTEX_NUM] = {};
 void (*visitfun)(OLGraph G, int v);

 //记录退出DFS函数之前完成搜索的顶点号
 int GFinished[MAX_VERTEX_NUM] = {};
 int GCount = ;

 #define D_OUT 0
 #define D_IN  1
 typedef enum DIRECTION
 {
     IN,
     OUT
 }DIRECTION;

 //////////////////////////////////////////////////////////////
 // 打印结点在图中的位置及结点信息
 //////////////////////////////////////////////////////////////
 void printvex(OLGraph G, int v)
 {
     printf("[%d]:%c\t", v, G.xlist[v].data);
     return ;
 }

 //////////////////////////////////////////////////////////////
 // direction is IN: 返回图G中以顶点位置为V的顶点为入度的第一个结点
 // direction is OUT: 返回图G中以顶点位置为V的顶点为出度的第一个结点
 //////////////////////////////////////////////////////////////
 int FirstAdjVex(OLGraph G, int v, int direction)
 {
     if(direction == IN){
         return (G.xlist[v].firstin)?G.xlist[v].firstin->tailvex:-;
     }else if(direction == OUT){
         return (G.xlist[v].firstout)?G.xlist[v].firstout->headvex:-;
     }else{
         return -;
     }
 }

 //////////////////////////////////////////////////////////////
 // direction is IN: G中位置w是以v为入度的结点， 返回下一个以v为入度的结点
 // direction is OUT: G中位置w是以v为出度的结点， 返回下一个以v为出度的结点
 //////////////////////////////////////////////////////////////
 int NextAdjVex(OLGraph G, int v, int w, int direction)
 {
     int ret = -;
     if(direction == IN){
         ArcBox *fi = NULL;
         fi = G.xlist[v].firstin;
         while(fi)
         {
             if(fi->tailvex == w)
                 break;
             fi = fi->hlink;
         }
         if(fi && (fi=fi->hlink)){
             ret = fi->tailvex;
         }else{
             ret = -;
         }
     }else if(direction == OUT){
         ArcBox *fo = NULL;
         fo = G.xlist[v].firstout;
         while(fo)
         {
             if(fo->headvex == w)
                 break;
             fo = fo->tlink;
         }
         if(fo && (fo=fo->tlink)){
             ret = fo->headvex;
         }else{
             ret = -;
         }
     }
     return ret;
 }
 //////////////////////////////////////////////////////////////
 // direction is IN :从第v个顶点出发, 沿着以v为入度的顶点的方式, 递归地深度优先遍历图G
 // direction is OUT :从第v个顶点出发, 沿着以v为出度的顶点的方式, 递归地深度优先遍历图G
 //////////////////////////////////////////////////////////////
 void DFS(OLGraph G, int v, int direction)
 {
     GVisited[v] = ;
     printvex(G, v);
     int w = ;
     for(w=FirstAdjVex(G,v,direction); w>=; w=NextAdjVex(G, v, w, direction))
     {
         if(!GVisited[w]){
             DFS(G, w, direction);
         }
     }
     GFinished[GCount++] = v;
 }

 //////////////////////////////////////////////////////////////
 // 1 从第一个出发,对图G作深度优先遍历并记录下退出DFS函数的顺序
 // 2 从最后一个退出DFS函数的顶点出发， 反方向对图G作深度优先遍历并求出图的强连通分量
 //////////////////////////////////////////////////////////////
 void DFSTraverse(OLGraph G, void (*visitfun)(OLGraph G, int v))
 {
     visitfun = printvex;
     int v = ;
     int index = ;

     printf("\n深度优先搜索(以第一个顶点为尾的弧进行深度优先搜索遍历):\n");
     //访问标志数组初始化
     for(v=; v<G.vexnum; v++)
     {
         GVisited[v] = ;
         GFinished[v] = ;
     }
     GCount = ;

     for(v=; v<G.vexnum; v++)
     {
         if(!GVisited[v]){
             DFS(G, v, OUT);
         }
     }

     printf("\n退出DFS函数的次序location和顶点位置index为:\n");
     for(v=; v<GCount; v++)
     {
         printf("[location:%d, index:%d] ", v, GFinished[v]);
     }
     printf("\n");

     printf("深度优先搜索(从最后完成搜索的顶点出发，沿着以该顶点为头的弧作逆向的深度优先搜索遍历):");
     //访问标志数组初始化
     for(v=; v<G.vexnum; v++)
     {
         GVisited[v] = ;
     }
     for(v=; v<GCount; v++)
     {
         index = GFinished[GCount--v];
         if(!GVisited[index]){
             printf("\n强连通分量:");
             DFS(G, index, IN);
         }
     }
     printf("\n");
 }

 int main(int argc, char *argv[])
 {
     OLGraph G;
     if(CreateGraph(&G) > -){
         printG(G);
     }
     DFSTraverse(G, printvex);
 }

有向图(十字链表存储)的强连通分量

代码运行

Example01

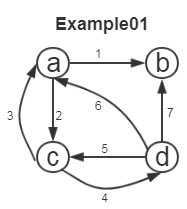
[jennifer@localhost Data.Structure]$ ./a.out
输入图类型: +有向图(0), -有向网(1), -无向图(2), -无向网(3): 0

以十字链表作为图的存储结构创建有向图:
输入顶点数，弧数，其他信息标志位: 4,7,0
输入第1个顶点: a
输入第2个顶点: b
输入第3个顶点: c
输入第4个顶点: d
输入第1条弧(顶点1, 顶点2): a,b
输入第2条弧(顶点1, 顶点2): a,c
输入第3条弧(顶点1, 顶点2): c,a
输入第4条弧(顶点1, 顶点2): c,d
输入第5条弧(顶点1, 顶点2): d,c
输入第6条弧(顶点1, 顶点2): d,a
输入第7条弧(顶点1, 顶点2): d,b

打印图结点
类型：有向图；顶点数 4, 弧数 7
a: {hlink=(3,d)->(0,a); (2,c)->(0,a); }        {tlink=(0,a)->(2,c); (0,a)->(1,b); }
b: {hlink=(3,d)->(1,b); (0,a)->(1,b); }        {tlink=}
c: {hlink=(3,d)->(2,c); (0,a)->(2,c); }        {tlink=(2,c)->(3,d); (2,c)->(0,a); }
d: {hlink=(2,c)->(3,d); }        {tlink=(3,d)->(1,b); (3,d)->(0,a); (3,d)->(2,c); }

深度优先搜索(以第一个顶点为尾的弧进行深度优先搜索遍历):
[]:a    []:c    []:d    []:b
退出DFS函数的次序location和顶点位置index为:
[location:0, index:1] [location:1, index:3] [location:2, index:2] [location:3, index:0]
深度优先搜索(从最后完成搜索的顶点出发，沿着以该顶点为头的弧作逆向的深度优先搜索遍历):
强连通分量:[]:a    []:d    []:c
强连通分量:[]:b
[jennifer@localhost Data.Structure]$ 

Example01

Example02

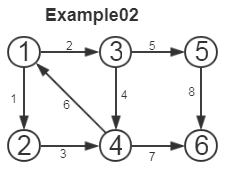
[jennifer@localhost blogs]$ ./a.out
输入图类型: +有向图(0), -有向网(1), -无向图(2), -无向网(3): 0

以十字链表作为图的存储结构创建有向图:
输入顶点数，弧数，其他信息标志位: 6,8,0
输入第1个顶点: 1
输入第2个顶点: 2
输入第3个顶点: 3
输入第4个顶点: 4
输入第5个顶点: 5
输入第6个顶点: 6
输入第1条弧(顶点1, 顶点2): 1,2
输入第2条弧(顶点1, 顶点2): 1,3
输入第3条弧(顶点1, 顶点2): 2,4
输入第4条弧(顶点1, 顶点2): 3,4
输入第5条弧(顶点1, 顶点2): 3,5
输入第6条弧(顶点1, 顶点2): 4,1
输入第7条弧(顶点1, 顶点2): 4,7
输入第8条弧(顶点1, 顶点2): 5,6

打印图结点
类型：有向图；顶点数 6, 弧数 8
1: {hlink=(3,4)->(0,1); }        {tlink=(0,1)->(2,3); (0,1)->(1,2); }
2: {hlink=(0,1)->(1,2); }        {tlink=(1,2)->(3,4); }
3: {hlink=(0,1)->(2,3); }        {tlink=(2,3)->(4,5); (2,3)->(3,4); }
4: {hlink=(2,3)->(3,4); (1,2)->(3,4); }        {tlink=(3,4)->(-1,<); (3,4)->(0,1); }
5: {hlink=(2,3)->(4,5); }        {tlink=(4,5)->(5,6); }
6: {hlink=(4,5)->(5,6); }        {tlink=}

深度优先搜索(以第一个顶点为尾的弧进行深度优先搜索遍历):
[]:1    []:3    []:5    []:6    []:4    []:2
退出DFS函数的次序location和顶点位置index为:
[location:0, index:5] [location:1, index:4] [location:2, index:3] [location:3, index:2] [location:4, index:1] [location:5, index:0]
深度优先搜索(从最后完成搜索的顶点出发，沿着以该顶点为头的弧作逆向的深度优先搜索遍历):
强连通分量:[]:1    []:4    []:3    []:2
强连通分量:[]:5
强连通分量:[]:6
[jennifer@localhost blogs]$ 

Example02

Example03

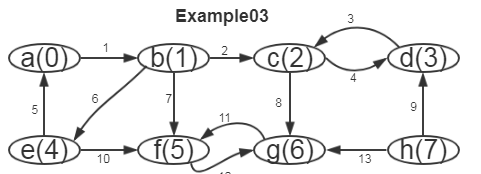
[jennifer@localhost blogs]$ ./a.out
输入图类型: +有向图(0), -有向网(1), -无向图(2), -无向网(3): 0

以十字链表作为图的存储结构创建有向图:
输入顶点数，弧数，其他信息标志位: 8,13,0
输入第1个顶点: a
输入第2个顶点: b
输入第3个顶点: c
输入第4个顶点: d
输入第5个顶点: e
输入第6个顶点: f
输入第7个顶点: g
输入第8个顶点: h
输入第1条弧(顶点1, 顶点2): a,b
输入第2条弧(顶点1, 顶点2): b,c
输入第3条弧(顶点1, 顶点2): d,c
输入第4条弧(顶点1, 顶点2): c,d
输入第5条弧(顶点1, 顶点2): e,a
输入第6条弧(顶点1, 顶点2): b,e
输入第7条弧(顶点1, 顶点2): b,f
输入第8条弧(顶点1, 顶点2): c,g
输入第9条弧(顶点1, 顶点2): h,d
输入第10条弧(顶点1, 顶点2): e,f
输入第11条弧(顶点1, 顶点2): g,f
输入第12条弧(顶点1, 顶点2): f,g
输入第13条弧(顶点1, 顶点2): h,g

打印图结点
类型：有向图；顶点数 8, 弧数 13
a: {hlink=(4,e)->(0,a); }        {tlink=(0,a)->(1,b); }
b: {hlink=(0,a)->(1,b); }        {tlink=(1,b)->(5,f); (1,b)->(4,e); (1,b)->(2,c); }
c: {hlink=(3,d)->(2,c); (1,b)->(2,c); }        {tlink=(2,c)->(6,g); (2,c)->(3,d); }
d: {hlink=(7,h)->(3,d); (2,c)->(3,d); }        {tlink=(3,d)->(2,c); }
e: {hlink=(1,b)->(4,e); }        {tlink=(4,e)->(5,f); (4,e)->(0,a); }
f: {hlink=(6,g)->(5,f); (4,e)->(5,f); (1,b)->(5,f); }        {tlink=(5,f)->(6,g); }
g: {hlink=(7,h)->(6,g); (5,f)->(6,g); (2,c)->(6,g); }        {tlink=(6,g)->(5,f); }
h: {hlink=}        {tlink=(7,h)->(6,g); (7,h)->(3,d); }

深度优先搜索(以第一个顶点为尾的弧进行深度优先搜索遍历):
[]:a    []:b    []:f    []:g    []:e    []:c    []:d    []:h
退出DFS函数的次序location和顶点位置index为:
[location:0, index:6] [location:1, index:5] [location:2, index:4] [location:3, index:3] [location:4, index:2] [location:5, index:1] [location:6, index:0] [location:7, index:7]
深度优先搜索(从最后完成搜索的顶点出发，沿着以该顶点为头的弧作逆向的深度优先搜索遍历):
强连通分量:[]:h
强连通分量:[]:a    []:e    []:b
强连通分量:[]:c    []:d
强连通分量:[]:f    []:g
[jennifer@localhost blogs]$ 

Example03

Example04

[jennifer@localhost blogs]$ ./a.out
输入图类型: +有向图(0), -有向网(1), -无向图(2), -无向网(3): 0

以十字链表作为图的存储结构创建有向图:
输入顶点数，弧数，其他信息标志位: 10,15
输入第1个顶点: ^C
[jennifer@localhost blogs]$ ./a.out
输入图类型: +有向图(0), -有向网(1), -无向图(2), -无向网(3): 0

以十字链表作为图的存储结构创建有向图:
输入顶点数，弧数，其他信息标志位: 10,15,0
输入第1个顶点: 0
输入第2个顶点: 1
输入第3个顶点: 2
输入第4个顶点: 3
输入第5个顶点: 4
输入第6个顶点: 5
输入第7个顶点: 6
输入第8个顶点: 7
输入第9个顶点: 8
输入第10个顶点: 9
输入第1条弧(顶点1, 顶点2): 9,2
输入第2条弧(顶点1, 顶点2): 7,9
输入第3条弧(顶点1, 顶点2): 2,7
输入第4条弧(顶点1, 顶点2): 2,1
输入第5条弧(顶点1, 顶点2): 2,4
输入第6条弧(顶点1, 顶点2): 7,4
输入第7条弧(顶点1, 顶点2): 1,8
输入第8条弧(顶点1, 顶点2): 0,1
输入第9条弧(顶点1, 顶点2): 1,0
输入第10条弧(顶点1, 顶点2): 0,4
输入第11条弧(顶点1, 顶点2): 8,5
输入第12条弧(顶点1, 顶点2): 5,0
输入第13条弧(顶点1, 顶点2): 4,3
输入第14条弧(顶点1, 顶点2): 3,4
输入第15条弧(顶点1, 顶点2): 5,6

打印图结点
类型：有向图；顶点数 10, 弧数 15
0: {hlink=(5,5)->(0,0); (1,1)->(0,0); }        {tlink=(0,0)->(4,4); (0,0)->(1,1); }
1: {hlink=(0,0)->(1,1); (2,2)->(1,1); }        {tlink=(1,1)->(0,0); (1,1)->(8,8); }
2: {hlink=(9,9)->(2,2); }        {tlink=(2,2)->(4,4); (2,2)->(1,1); (2,2)->(7,7); }
3: {hlink=(4,4)->(3,3); }        {tlink=(3,3)->(4,4); }
4: {hlink=(3,3)->(4,4); (0,0)->(4,4); (7,7)->(4,4); (2,2)->(4,4); }        {tlink=(4,4)->(3,3); }
5: {hlink=(8,8)->(5,5); }        {tlink=(5,5)->(6,6); (5,5)->(0,0); }
6: {hlink=(5,5)->(6,6); }        {tlink=}
7: {hlink=(2,2)->(7,7); }        {tlink=(7,7)->(4,4); (7,7)->(9,9); }
8: {hlink=(1,1)->(8,8); }        {tlink=(8,8)->(5,5); }
9: {hlink=(7,7)->(9,9); }        {tlink=(9,9)->(2,2); }

深度优先搜索(以第一个顶点为尾的弧进行深度优先搜索遍历):
[]:0    []:4    []:3    []:1    []:8    []:5    []:6    []:2    []:7    []:9
退出DFS函数的次序location和顶点位置index为:
[location:0, index:3] [location:1, index:4] [location:2, index:6] [location:3, index:5] [location:4, index:8] [location:5, index:1] [location:6, index:0] [location:7, index:9] [location:8, index:7] [location:9, index:2]
深度优先搜索(从最后完成搜索的顶点出发，沿着以该顶点为头的弧作逆向的深度优先搜索遍历):
强连通分量:[]:2    []:9    []:7
强连通分量:[]:0    []:5    []:8    []:1
强连通分量:[]:6
强连通分量:[]:4    []:3
[jennifer@localhost blogs]$ 

Example04