bzoj 1013 [JSOI2008]球形空间产生器sphere（高斯消元）

1013: [JSOI2008]球形空间产生器sphere

Time Limit: 1 Sec  Memory Limit: 162 MB
Submit: 3584  Solved: 1863
[Submit][Status][Discuss]

Description

有一个球形空间产生器能够在n维空间中产生一个坚硬的球体。现在，你被困在了这个n维球体中，你只知道球面上n+1个点的坐标，你需要以最快的速度确定这个n维球体的球心坐标，以便于摧毁这个球形空间产生器。

Input

第一行是一个整数，n。接下来的n+1行，每行有n个实数，表示球面上一点的n维坐标。每一个实数精确到小数点后6位，且其绝对值都不超过20000。

Output

有且只有一行，依次给出球心的n维坐标（n个实数），两个实数之间用一个空格隔开。每个实数精确到小数点后3位。数据保证有解。你的答案必须和标准输出一模一样才能够得分。

Sample Input

2
0.0 0.0
-1.0 1.0
1.0 0.0

Sample Output

0.500 1.500

HINT

数据规模：

对于40%的数据，1<=n<=3

对于100%的数据，1<=n<=10

提示：给出两个定义：

1、 球心：到球面上任意一点距离都相等的点。

2、 距离：设两个n为空间上的点A, B的坐标为(a1, a2, …, an), (b1, b2, …, bn)，则AB的距离定义为：dist = sqrt( (a1-b1)^2 + (a2-b2)^2 + … + (an-bn)^2 )

Source

【思路】

高斯消元

列方程：设两点坐标为a[]，b[]，且x[]为球心坐标。则满足：

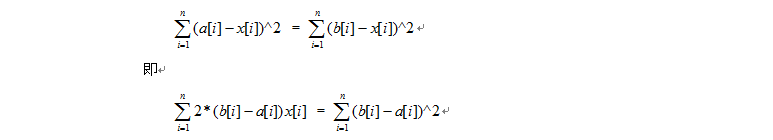
每两个相邻点满足该式即可保证x为球心，所以只需要解n个方程。

然后高斯消元解方程即可。

【代码】

 #include<cstdio>
 #include<cmath>
 #include<iostream>
 using namespace std;

 typedef double dl;
 const int N = ;

 dl A[N][N],a[N][N];
 int n;

 void gause() {
     int i,j,k,r;
     for(i=;i<n;i++) {                        //消元
         r=i;
         for(j=i+;j<n;j++)
             if(fabs(A[j][i])>fabs(A[r][i])) r=j;
         if(r!=i) for(j=;j<=n;j++) swap(A[r][j],A[i][j]);
         for(j=n;j>=i;j--)                   //使A[k][i]为0
             for(k=i+;k<n;k++)
                 A[k][j]-=A[k][i]/A[i][i]*A[i][j];
     }
     for(i=n-;i>=;i--) {                    //回代
         for(j=i+;j<n;j++)
             A[i][n]-=A[j][n]*A[i][j];
         A[i][n]/=A[i][i];
     }
 }

 int main() {
     scanf("%d",&n);
     for(int i=;i<=n;i++) for(int j=;j<n;j++)
         scanf("%lf",&a[i][j]);
     for(int i=;i<n;i++) {                    //构造方程组
         for(int j=;j<n;j++) A[i][j]=*(a[i+][j]-a[i][j]);
         for(int j=;j<n;j++) A[i][n]+=a[i+][j]*a[i+][j]-a[i][j]*a[i][j];
     }
     gause();
     printf("%.3lf",A[][n]);
     for(int i=;i<n;i++) printf(" %.3lf",A[i][n]);
     return ;
 }