Codeforces 446-C DZY Loves Fibonacci Numbers 同余 线段树 斐波那契数列

C. DZY Loves Fibonacci Numbers

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In mathematical terms, the sequence F_n of Fibonacci numbers is defined by the recurrence relation

F₁ = 1; F₂ = 1; F_n = F_n - 1 + F_n - 2 (n > 2).

DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a₁, a₂, ..., a_n. Moreover, there are m queries, each query has one of the two types:

1. Format of the query "1 l r". In reply to the query, you need to add F_{i - l + 1} to each element a_i, where l ≤ i ≤ r.
2. Format of the query "2 l r". In reply to the query you should output the value of 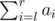modulo 1000000009 (10⁹ + 9).

Help DZY reply to all the queries.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000). The second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹) — initial array a.

Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.

Output

For each query of the second type, print the value of the sum on a single line.

Sample test(s)

Input

4 4
1 2 3 4
1 1 4
2 1 4
1 2 4
2 1 3

Output

17
12

Note

After the first query, a = [2, 3, 5, 7].

For the second query, sum = 2 + 3 + 5 + 7 = 17.

After the third query, a = [2, 4, 6, 9].

For the fourth query, sum = 2 + 4 + 6 = 12.

官方题解：

As we know,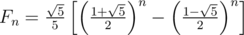

Fortunately, we find that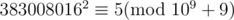

So,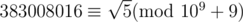

With multiplicative inverse, we find,

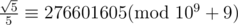
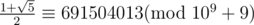
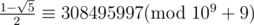
Now,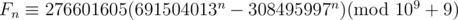

As you see, we can just maintain the sum of a Geometric progression

This is a simple problem which can be solved with segment tree in .

这道题是Fibonacci数列通项公式的应用，比较经典。至少我是不可能想到斐波那契数列与等比数列有任何关联。还有一点，在程序内层循环中，快速幂的时间复杂度是不容忽视的（估计是线段树写抽了），这里既然公比恒定，可先与处理一下。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
#define MAXN 310000
#define MAXT 1210000
#define MOD 1000000009
#define lch (now<<1)
#define rch (now<<1^1)
void nextInt(int &x)
{
        char ch;
        x=;
        while (ch=getchar(),ch>''||ch<'');
        do
                x=x*+ch-'';
        while (ch=getchar(),ch<=''&&ch>='');
}
int n,m;
typedef long long qword;
int num[MAXN];
qword val1,val2,val3,val4,val3_n,val4_n,mod;
qword val3_pow[MAXN],val4_pow[MAXN];
qword pow_mod(qword x,qword y,int mod)
{
        qword ret=;
        while (y)
        {
                if (y&)ret=ret*x%mod;
                x=x*x%mod;
                y>>=;
        }
        return ret;
}
struct node
{
        int l,r;
        qword sum;
        qword inc3,inc4;
}tree[MAXT];
inline void update_sum_3(int now,int inc3)
{
        qword temp;
        temp=inc3*(val3_pow[tree[now].r-tree[now].l+]-)%MOD*val3_n%MOD;
    //    temp=(temp+MOD)%MOD;
        tree[now].sum=(tree[now].sum+temp)%MOD;
}
inline void update_sum_4(int now,int inc4)
{
        qword temp;
        temp=inc4*(val4_pow[tree[now].r-tree[now].l+]-)%MOD*val4_n%MOD;
        temp=(-temp+MOD)%MOD;
        tree[now].sum=(tree[now].sum+temp)%MOD;
}
inline void down(int now)
{
        if (tree[now].l==tree[now].r)
        {
                if (tree[now].inc3)
                {
                        tree[now].inc3=;
                }
                if (tree[now].inc4)
                {
                        tree[now].inc4=;
                }
                return ;
        }
        if (tree[now].inc3)
        {
                qword temp;
                tree[lch].inc3=(tree[lch].inc3+tree[now].inc3)%MOD;
        //        tree[lch].inc3%=MOD;
                update_sum_3(lch,tree[now].inc3);
                tree[rch].inc3+=temp=val3_pow[tree[lch].r-tree[lch].l+]*tree[now].inc3%MOD;
                tree[rch].inc3%=MOD;
                update_sum_3(rch,temp);
                tree[now].inc3=;
        }
        if (tree[now].inc4)
        {
                qword temp;
                tree[lch].inc4+=tree[now].inc4;
                tree[lch].inc4%=MOD;
                update_sum_4(lch,tree[now].inc4);
                tree[rch].inc4+=temp=val4_pow[tree[lch].r-tree[lch].l+]*tree[now].inc4%MOD;
                tree[rch].inc4%=MOD;
                update_sum_4(rch,temp);
                tree[now].inc4=;
        }
}
inline void update(int now)
{
        if (tree[now].l!=tree[now].r)
                tree[now].sum=(tree[lch].sum+tree[rch].sum)%MOD;
}
void init()
{
        /*//{{{
        int i;
           for (i=1;i<MOD;i++)
           {
           if ((qword)i*i%MOD==5)
           {
           val1=i;
           break;
           }
           }
           cout<<val1<<endl;
           for (i=1;i<MOD;i++)
           {
           if ((qword)i*5%MOD==val1)
           {
           val2=i;
           break;
           }
           }
           cout<<val2<<endl;
           for (i=1;i<MOD;i++)
           {
           if ((qword)i*2%MOD-1==val1)
           {
           val3=i;
           break;
           }
           }
           cout<<val3<<endl;
           for (i=1;i<MOD;i++)
           {
           if ((qword)i*2-1==(-val1+MOD)%MOD)
           {
           val4=i;
           break;
           }
           }
           cout<<val4<<endl;//}}}*/
        val1=;//sqrt(5)
        val2=;//sqrt(5)/5
        val3=;//(1+sqrt(5))/2
        val4=;//(1-sqrt(5))/2
        int i;
        qword temp=val3;
        val3_pow[]=;
        for (i=;i<MAXN;i++)
        {
                val3_pow[i]=val3_pow[i-]*val3%MOD;;
        }
        val4_pow[]=;
        for (i=;i<MAXN;i++)
        {
                val4_pow[i]=val4_pow[i-]*val4%MOD;
        }
        val3_n=pow_mod(val3-,MOD-,MOD);
        val4_n=pow_mod(val4-,MOD-,MOD);
        //fib(n)=val2*(val3^n-val4^n);
}
void build_tree(int now,int l,int r)
{
        tree[now].l=l;
        tree[now].r=r;
        if (l==r)
        {
                tree[now].sum=num[l];
                return ;
        }
        int mid=(l+r)/;
        build_tree(lch,l,mid);
        build_tree(rch,mid+,r);
        update(now);
}
void add_val(int now,int l,int r,int rk)
{
        if (tree[now].l==l&&tree[now].r==r)
        {
                qword temp;
                temp=val2*val3%MOD*val3_pow[rk]%MOD;
                tree[now].inc3=(tree[now].inc3+temp)%MOD;
                update_sum_3(now,temp);
                temp=val2*val4%MOD*val4_pow[rk]%MOD;
                tree[now].inc4=(tree[now].inc4+temp)%MOD;
                update_sum_4(now,temp);
                return ;
        }
        down(now);
        int mid=(tree[now].l+tree[now].r)>>;
        if (r<=mid)
        {
                add_val(lch,l,r,rk);
                update(now);
                return ;
        }
        if (mid<l)
        {
                add_val(rch,l,r,rk);
                update(now);
                return ;
        }
        add_val(lch,l,mid,rk);
        add_val(rch,mid+,r,rk-l+mid+);
        update(now);
}
//ok
qword query(int now,int l,int r)
{
        if (tree[now].l==l&&tree[now].r==r)
        {
                return tree[now].sum;
        }
        down(now);
        int mid=(tree[now].l+tree[now].r)>>;
        if (r<=mid)
                return query(lch,l,r);
        if (mid<l)
                return query(rch,l,r);
        return (query(lch,l,mid)+query(rch,mid+,r))%MOD;
}

int main()
{
        freopen("input.txt","r",stdin);
        freopen("output.txt","w",stdout);
        //scanf("%d%d",&n,&m);
        nextInt(n);
        nextInt(m);
        int i,j,k,x,y,z;
        init();
        for (i=;i<=n;i++)
                nextInt(num[i]);
        build_tree(,,n);
        while (m--)
        {
                nextInt(x);
                nextInt(y);
                nextInt(z);
                if (x==)
                {
                        add_val(,y,z,);
                }else
                {
                        printf("%I64d\n",query(,y,z));
                }
        }
}