Gym 100187M-Heaviside Function

题意：给定函数： f(x) = θ(s1x - a1) + θ(s2x - a2) + ... + θ(snx - an), where si =  ± 1. Calculate its values for argument values x1, x2, ..., xm.其中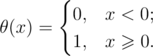      然后输入一系列si，ai，输出给定的f(xi)的值。

分析：之前一直没想到去化一化，其实就是分s=1和s=-1两种情况，然后分别算出θ(snx - an)==1有多少个，加起来就行了。Σ( ° △ °|||)︴

 #include <cstdio>
 #include <cmath>
 #include <cstring>
 #include <ctime>
 #include <iostream>
 #include <algorithm>
 #include <set>
 #include <vector>
 #include <sstream>
 #include <queue>
 #include <typeinfo>
 #include <fstream>
 #include <map>
 #include <stack>
 using namespace std;
 const int maxn=;
 int up[maxn],down[maxn],x;
 int main()
 {
     int n,m,s,a,cnt1=,cnt2=;
     scanf("%d",&n);
     for(int i=;i<=n;i++){
         scanf("%d%d",&s,&a);
         if(s>) up[cnt1++]=a;
         else down[cnt2++]=-a;
     }
     sort(up,up+cnt1);
     sort(down,down+cnt2);
     scanf("%d",&m);
     for(int i=;i<=m;i++){
         scanf("%d",&x);
         int ans1=upper_bound(up,up+cnt1,x)-up;
         int ans2=cnt2-(lower_bound(down,down+cnt2,x)-down);
         printf("%d\n",ans1+ans2);
     }
     return ;
 }