POJ 3608 Bridge Across Islands（旋转卡壳，两凸包最短距离）

Bridge Across Islands

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 7202		Accepted: 2113		Special Judge

Description

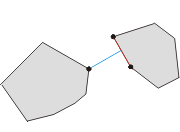
Thousands of thousands years ago there was a small kingdom located in the middle of the Pacific Ocean. The territory of the kingdom consists two separated islands. Due to the impact of the ocean current, the shapes of both the islands became convex polygons. The king of the kingdom wanted to establish a bridge to connect the two islands. To minimize the cost, the king asked you, the bishop, to find the minimal distance between the boundaries of the two islands.

Input

The input consists of several test cases.
Each test case begins with two integers N, M. (3 ≤ N, M ≤ 10000)
Each of the next N lines contains a pair of coordinates, which describes the position of a vertex in one convex polygon.
Each of the next M lines contains a pair of coordinates, which describes the position of a vertex in the other convex polygon.
A line with N = M = 0 indicates the end of input.
The coordinates are within the range [-10000, 10000].

Output

For each test case output the minimal distance. An error within 0.001 is acceptable.

Sample Input

4 4
0.00000 0.00000
0.00000 1.00000
1.00000 1.00000
1.00000 0.00000
2.00000 0.00000
2.00000 1.00000
3.00000 1.00000
3.00000 0.00000
0 0

Sample Output

1.00000

Source

POJ Founder Monthly Contest – 2008.06.29, Lei Tao

 

 

 

 

 

经典算法。

 

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
 
const double eps = 1e-;
int sgn(double x)
{
    if(fabs(x) < eps)return ;
    if(x < )return -;
    else return ;
}
struct Point
{
    double x,y;
    Point(double _x = 0.0,double _y = 0.0)
    {
        x = _x;
        y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x, y - b.y);
    }
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
    void input()
    {
        scanf("%lf%lf",&x,&y);
    }
};
struct Line
{
    Point s,e;
    Line(){}
    Line(Point _s,Point _e)
    {
        s = _s;
        e = _e;
    }
};
double dist(Point a,Point b)
{
    return sqrt((a-b)*(a-b));
}
Point NearestPointToLineSeg(Point P,Line L)
{
    Point result;
    double t = ((P-L.s)*(L.e-L.s))/((L.e-L.s)*(L.e-L.s));
    if(t >=  && t <= )
    {
        result.x = L.s.x + (L.e.x - L.s.x)*t;
        result.y = L.s.y + (L.e.y - L.s.y)*t;
    }
    else
    {
        if(dist(P,L.s) < dist(P,L.e))
            result = L.s;
        else result = L.e;
    }
    return result;
}
/*
 * 求凸包，Graham算法
 * 点的编号0~n-1
 * 返回凸包结果Stack[0~top-1]为凸包的编号
 */
const int MAXN = ;
Point list[MAXN];
int Stack[MAXN],top;
//相对于list[0]的极角排序
bool _cmp(Point p1,Point p2)
{
    double tmp = (p1-list[])^(p2-list[]);
    if(sgn(tmp) > )return true;
    else if(sgn(tmp) ==  && sgn(dist(p1,list[]) - dist(p2,list[])) <= )
        return true;
    else return false;
}
void Graham(int n)
{
    Point p0;
    int k = ;
    p0 = list[];
    //找最下边的一个点
    for(int i = ;i < n;i++)
    {
        if( (p0.y > list[i].y) || (p0.y == list[i].y && p0.x > list[i].x) )
        {
            p0 = list[i];
            k = i;
        }
    }
    swap(list[k],list[]);
    sort(list+,list+n,_cmp);
    if(n == )
    {
        top = ;
        Stack[] = ;
        return;
    }
    if(n == )
    {
        top = ;
        Stack[] = ;
        Stack[] = ;
        return ;
    }
    Stack[] = ;
    Stack[] = ;
    top = ;
    for(int i = ;i < n;i++)
    {
        while(top >  && sgn((list[Stack[top-]]-list[Stack[top-]])^(list[i]-list[Stack[top-]])) <= )
            top--;
        Stack[top++] = i;
    }
}
//点p0到线段p1p2的距离
double pointtoseg(Point p0,Point p1,Point p2)
{
    return dist(p0,NearestPointToLineSeg(p0,Line(p1,p2)));
}
//平行线段p0p1和p2p3的距离
double dispallseg(Point p0,Point p1,Point p2,Point p3)
{
    double ans1 = min(pointtoseg(p0,p2,p3),pointtoseg(p1,p2,p3));
    double ans2 = min(pointtoseg(p2,p0,p1),pointtoseg(p3,p0,p1));
    return min(ans1,ans2);
}
//得到向量a1a2和b1b2的位置关系
double Get_angle(Point a1,Point a2,Point b1,Point b2)
{
    Point t = b1 - ( b2 - a1 );
    return (a2-a1)^(t-a1);
}
//旋转卡壳，求两个凸包的最小距离
double rotating_calipers(Point p[],int np,Point q[],int nq)
{
    int sp = , sq = ;
    for(int i = ;i < np;i++)
        if(sgn(p[i].y - p[sp].y) < )
            sp = i;
    for(int i = ;i < nq;i++)
        if(sgn(q[i].y - q[sq].y) > )
            sq = i;
    double tmp;
    double ans = 1e99;
    for(int i = ;i < np;i++)
    {
        while(sgn(tmp = Get_angle(p[sp],p[(sp+)%np],q[sq],q[(sq+)%nq])) <  )
            sq = (sq + )%nq;
        if(sgn(tmp) == )
            ans = min(ans,dispallseg(p[sp],p[(sp+)%np],q[sq],q[(sq+)%nq]));
        else ans = min(ans,pointtoseg(q[sq],p[sp],p[(sp+)%np]));
        sp = (sp+)%np;
    }
    return ans;
}
 
double solve(Point p[],int n,Point q[],int m)
{
    return min(rotating_calipers(p,n,q,m),rotating_calipers(q,m,p,n));
}
Point p[MAXN],q[MAXN];
int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)==)
    {
        if(n ==  && m == )break;
        for(int i = ;i < n;i++)
            list[i].input();
        Graham(n);
        n = top;
        for(int i = ;i < n;i++)
            p[i] = list[Stack[i]];
        for(int i = ;i < m;i++)
            list[i].input();
        Graham(m);
        m = top;
        for(int i = ;i < m;i++)
            q[i] = list[Stack[i]];
        printf("%.5lf\n",solve(p,n,q,m));
    }
    return ;
}