【RL系列】Multi-Armed Bandit笔记——UCB策略与Gradient策略

本篇主要是为了记录UCB策略与Gradient策略在解决Multi-Armed Bandit问题时的实现方法，涉及理论部分较少，所以请先阅读Reinforcement Learning: An Introduction (Drfit) 的2.7，2.8的内容。为了更深入一点了解UCB策略，可以随后阅读下面这篇文章：

【RL系列】Multi-Armed Bandit笔记补充（二）—— UCB策略

UCB策略需要进行初始化工作，也就是说通常都会在进入训练之前先将每个动作都测试一变，保证每个动作被选择的次数都不为0且都会有一个初始的收益均值和置信上限，一般不会进行冷启动（冷启动的话，需要在开始时有一定的随机动作，会降低动作选择的效率）。我们可以设初始化函数UCBinitial，将其表现为Matlab：

function [Q UCBq] = UCBInitial(Q, Reward, UCBq)
% CurrentR: Current Reward
% CurrentA: Current Action
% RandK: K-Armed Bandit
% Q: Step-size Average Reward
% UCBq: Q + Upper Confidence Bound

RandK = length(Reward);
for n = 1:RandK
    CurrentA = n;
    CurrentR = normrnd(Reward(CurrentA), 1);

    Q(CurrentA) = (CurrentR - Q(CurrentA))*0.1 + Q(CurrentA);
    UCBq(CurrentA) = Q(CurrentA) + c*(2*log(n))^0.5;
end

　　

在训练中，UCB动作选择策略和置信上限值的更新策略可以写为：

% UCBq: Q + Upper Confidence Bound
% TotalCalls(Action): The Cumulative call times of Action
% c: Standard Deviation of reward in theorical analysis

[MAX CurrentA] = max(UCBq);
MAXq(CurrentA) = Q(CurrentA) + c*(2*log(n)/TotalCalls(CurrentA))^0.5;

　　

注意公式里的c应为理论上收益的标准差，但因为收益分布是一个黑箱，所以这个参数只能从实际实验中测试推断出来。这里我们假设收益标准差为1，所以为了实验效果，设c=1

接下来，我们就看一看UCB策略的测试效果吧。这里我们将其与epsilon-greedy策略进行对比（epsilon = 0.1），首先是Average Reward的测试结果：

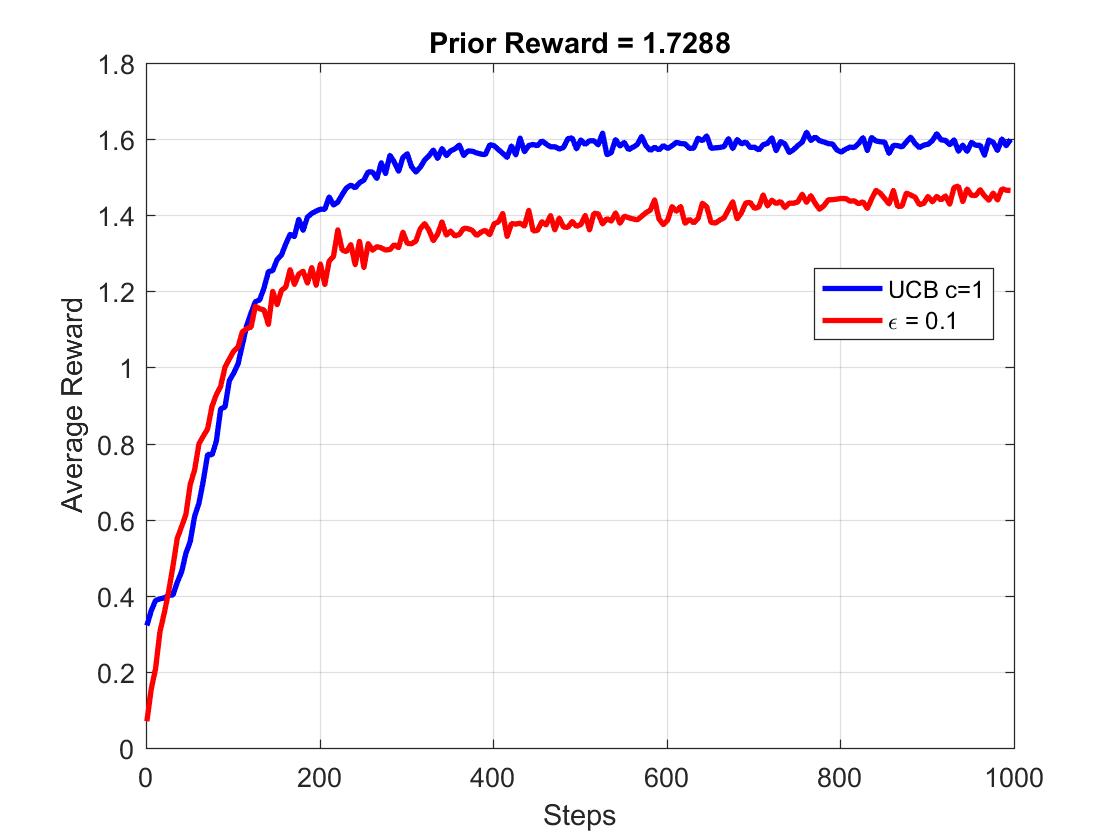
UCB算法在前1000次的学习中可以得到比epsilon-greedy更高的均值收益评价。那么这是否就代表了UCB策略可以更高概率的选取最优动作？下面我们看Optimal Action Rate的测试结果：

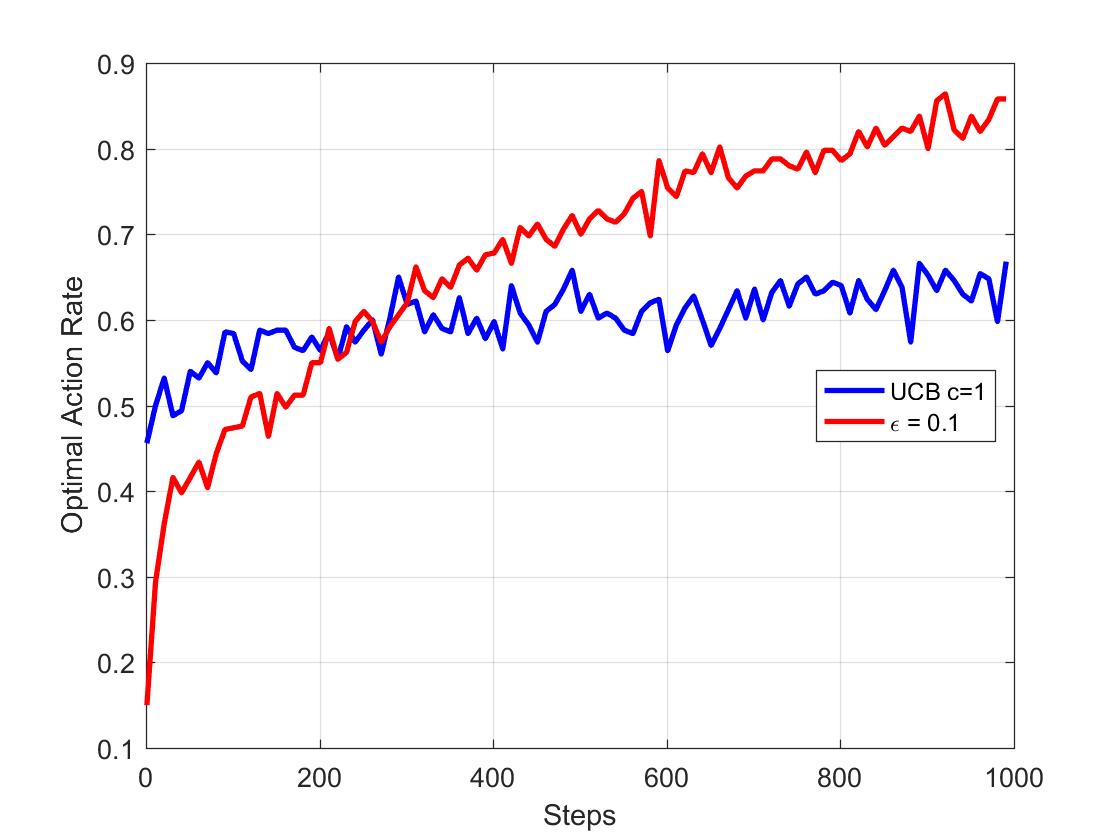
可以发现学习次数较少时，UCB策略可以比epsilon-greedy策略更快的获得较高概率的最优解，但最优动作选择率始终维持在60%左右，是低于epsilon-greedy策略在1000次学习时接近90%的数值的。这也直接的反映出UCB并不适合求解最优。那为什么最优动作选择率不高，但平均收益却较高呢？UCB大概率选择的优先动作通常是排名靠前的动作，也就是说动作选择并不一定是最优，但大概率是最佳的3个或2个动作中的一个，所以UCB也可用作二元分类策略，将表现较好的（大概率选择的动作）分为一类，表现较差的动作分为一类。

我们来看看UCB在分类中的表现，用80%分类准确度来进行评价。如果经过UCB策略学习后得到的估计收益均值中的前5位中有超过或等于4位与实际的收益均值相符的频率，以此近似为分类的准确度。也就是说，如果有10个bandit，我们将其分为两类，收益高的一类（前5个bandit）与收益低的一类（后5个bandit），80%分类准确度可以以此计算：估计的前5个bandit与实际的有超过4个相符的概率。用数学表述出来就是，如果有一个Reward集合R：

将其分为两类，按数值大小排序，前五名为一类，归为集合G，G是R的子集。通过学习估计出的G，称为A_G 。那么80%分类准确度可以表示为：

那么我们直接看结论吧：

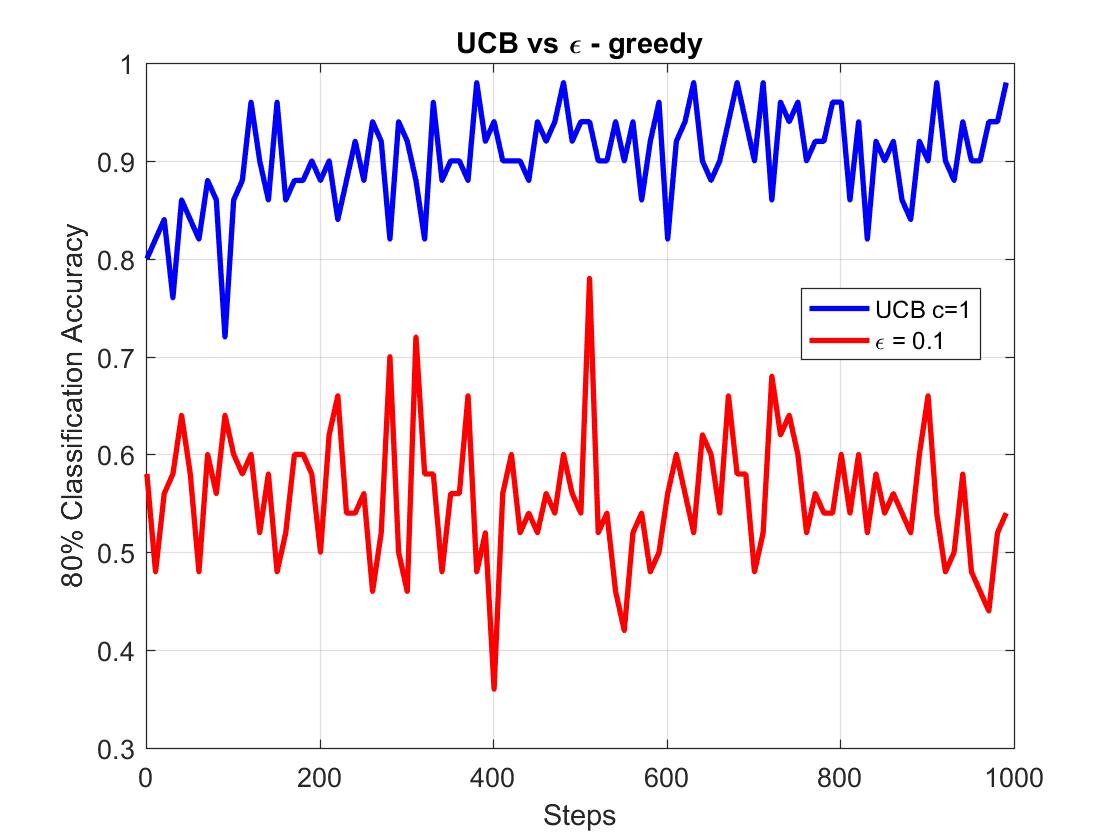
UCB的80%分类准确度始终在90%上下，而epsilon-greedy却只有50%左右。显然，UCB在这方面做的要好于epsilon-greedy。