NLM算法

non-Local Means 非局部均值

论文原文：http://www.ipol.im/pub/art/2011/bcm_nlm/?utm_source=doi

论文源代码：http://www.ipol.im/pub/art/2011/bcm_nlm/nlmeansC.tar.gz

NLM去噪：

NLM去噪算法实现 - 羽凌寒 - CSDN博客 https://blog.csdn.net/u011630458/article/details/51317415

NLM插值：

基于NLM的插值算法 - 羽凌寒 - CSDN博客 https://blog.csdn.net/u011630458/article/details/53469918

MATLAB工具包：

Toolbox Non-Local Means - File Exchange - MATLAB Central https://ww2.mathworks.cn/matlabcentral/fileexchange/13619-toolbox-non-local-means

【参考文献】

[1] Buades A,Coll B,Morel J M.A Review of Image Denoising Algorithms, with a New One[J]. Multiscale Modeling & Simulation,2005,4(2);490-530.

[2] 郭红涛. 广义非局部均值算法的图像去噪[J]. 计算机应用研究, 2015, 32(7):2218-2221.

[3] 刘哲, 黄世奇, 姜杰. 基于多尺度自相似性和非局部均值的单幅图像超分辨率方法[J]. 红外技术, 2017, 39(4).

【相关】

Image denoising with block-matching and 3D filtering_百度学术 BM3D

A fast non-local image denoising algorithm_百度学术

分析：

非局部均值滤波详解.doc https://max.book118.com/html/2016/1206/68911778.shtm

相似权重参数h的影响，h小权重分离大，更能保边。

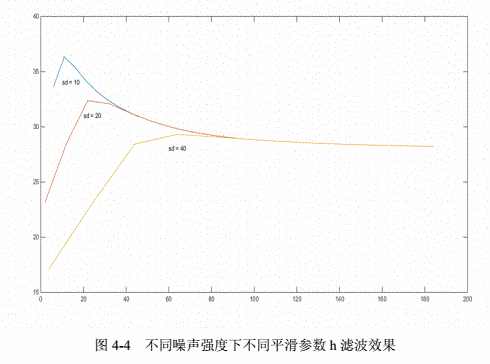
时间优化

1、基于积分图像

构造关于像素差值的积分图像。原图像与平移t=y-x后的图像间欧式距离为：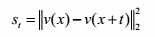

2、基于傅里叶变换

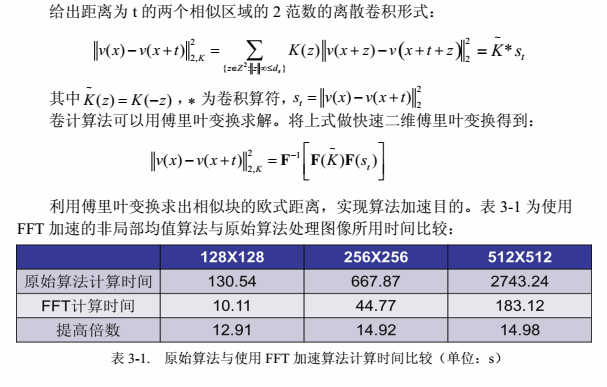
【其他资料】

【图文】非局部均值滤波_百度文库 https://wenku.baidu.com/view/fc819b3b5022aaea988f0f1d.html

图像保边滤波算法集锦--非局部均值NLM滤波器 - Trent1985的专栏 - CSDN博客 https://blog.csdn.net/trent1985/article/details/82900592

非局部均值滤波算法 - Frankgoogle的博客 - CSDN博客 https://blog.csdn.net/frankgoogle/article/details/52209901

图像去燥中 非局部均值滤波的简单原理 - phoenixtree7的专栏 - CSDN博客 https://blog.csdn.net/phoenixtree7/article/details/51802569

【图像算法】NLM降噪 - Image - CSDN博客 https://blog.csdn.net/jaych/article/details/54562593

非局部均值滤波原理 Non-local means filter 【从零起步完全教程】 - 照玄 - CSDN博客 https://blog.csdn.net/sac761/article/details/76544791

使用自相似度驱动混合的带细节保留的非局部均值图像去噪的制作方法 http://www.xjishu.com/zhuanli/55/201580044895.html

【细节步骤分析】

非局部均值去噪的一点问题_蒋含禄_新浪博客 http://blog.sina.com.cn/s/blog_6cba908f0100t24j.html