梯度下降之随机梯度下降 -minibatch 与并行化方法

问题的引入：

考虑一个典型的有监督机器学习问题，给定m个训练样本S={x^(i),y⁽ⁱ⁾}，通过经验风险最小化来得到一组权值w，则现在对于整个训练集待优化目标函数为：

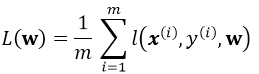
其中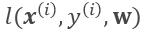为单个训练样本（x^(i),y⁽ⁱ⁾）的损失函数，单个样本的损失表示如下：

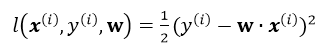
引入L2正则，即在损失函数中引入，那么最终的损失为：

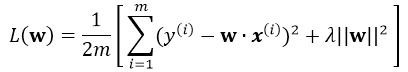
注意单个样本引入损失为（并不用除以m）：

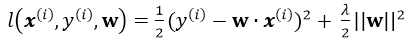
正则化的解释

这里的正则化项可以防止过拟合，注意是在整体的损失函数中引入正则项，一般的引入正则化的形式如下：

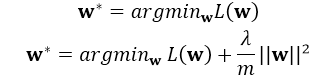
其中L(w)为整体损失，这里其实有：

这里的 C即可代表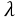，比如以下两种不同的正则方式：

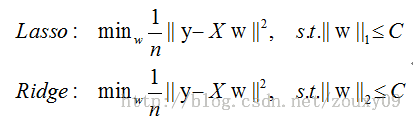
下面给一个二维的示例图：我们将模型空间限制在w的一个L1-ball 中。为了便于可视化，我们考虑两维的情况，在(w1, w2)平面上可以画出目标函数的等高线，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解

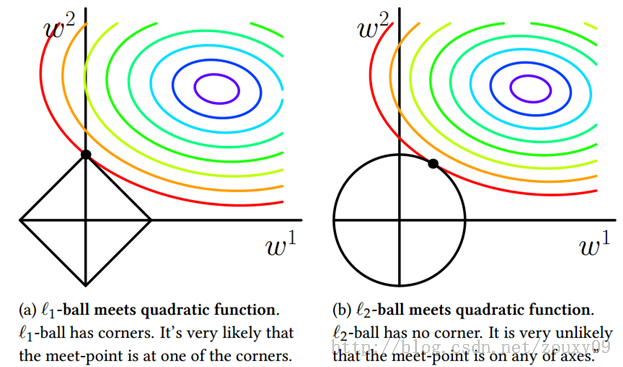
可以看到，L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，而目标函数的测地线除非位置摆得非常好，大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性，例如图中的相交点就有w1=0，而更高维的时候（想象一下三维的L1-ball 是什么样的？）除了角点以外，还有很多边的轮廓也是既有很大的概率成为第一次相交的地方，又会产生稀疏性，相比之下，L2-ball 就没有这样的性质，因为没有角，所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。

因此，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

Batch Gradient Descent

有了以上基本的优化公式，就可以用Gradient Descent 来对公式进行求解，假设w的维度为n，首先来看标准的Batch Gradient Descent算法：

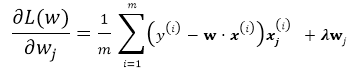
repeat until convergency{

　　for j=1;j<n ; j++:

　　　　

}

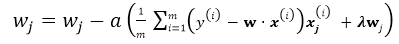
这里的批梯度下降算法是每次迭代都遍历所有样本，由所有样本共同决定最优的方向。

stochastic Gradient Descent

随机梯度下降就是每次从所有训练样例中抽取一个样本进行更新，这样每次都不用遍历所有数据集，迭代速度会很快，但是会增加很多迭代次数，因为每次选取的方向不一定是最优的方向.

repeat until convergency{

　　random choice j from all m training example：

　　　　

}

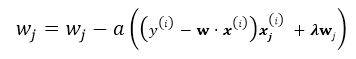
mini-batch Gradient Descent

这是介于以上两种方法的折中，每次随机选取大小为b的mini-batch(b<m), b通常取10，或者(2...100),这样既节省了计算整个批量的时间，同时用mini-batch计算的方向也会更加准确。

repeat until convergency{

　　for j=1;j<n ; j+=b:

　　　　

}

最后看并行化的SGD：

若最后的v达到收敛条件则结束执行，否则回到第一个for循环继续执行，该方法同样适用于minibatch gradient descent。