POJ 2528 区间染色，求染色数目，离散化

Mayor's posters

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 47905		Accepted: 13903

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:

• Every candidate can place exactly one poster on the wall.
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
• The wall is divided into segments and the width of each segment is one byte.
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.

 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed.

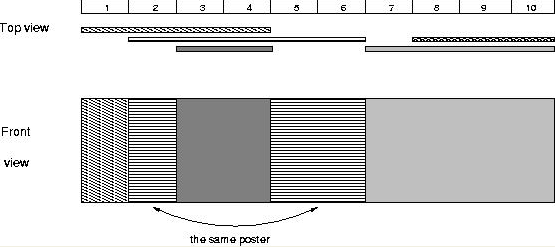
The picture below illustrates the case of the sample input.

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

Source

Alberta Collegiate Programming Contest 2003.10.18

 

 

题目意思：

给一个木板，宽度分为单位为1的段，贴n张海报，海报从l到r，高度等于木板的高度，问最终能看到多少张海报。

 

 

思路：

若每张海报都有一个特定的颜色用数字表示，那么问题就转变为从minl---maxr区间内有多少不同的数字，那么就是线段树区间更新的模型了。

l r最大为10000000，建树的话还要乘上4，很明显爆空间，需要离散化，离散化的时候不能是普通的离散化，需要考虑边界问题，离散化后求染色数目即可。

 

 

代码：

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <iostream>
 #include <vector>
 #include <queue>
 #include <cmath>
 #include <set>
 using namespace std;

 #define N 40005
 #define ll root<<1
 #define rr root<<1|1
 #define mid (a[root].l+a[root].r)/2

 int max(int x,int y){return x>y?x:y;}
 int min(int x,int y){return x<y?x:y;}
 int abs(int x,int y){return x<?-x:x;}

 int n;
 int x[N];
 int m;

 int bin_s(int key){
     int l=, r=m-;
     while(l<=r){
         int mm=(l+r)/;
         if(x[mm]==key) return mm;
         if(x[mm]>key) r=mm-;
         else if(x[mm]<key) l=mm+;
     }
 }

 struct Line{
     int l, r;
 }line[N];

 struct node{
     int l, r, val;
     bool f;
 }a[N*];

 void build(int l,int r,int root){
     a[root].l=l;
     a[root].r=r;
     a[root].val=-;
     if(l==r) return;
     build(l,mid,ll);
     build(mid+,r,rr);
 }

 void down(int root){
     if(a[root].val>&&a[root].l!=a[root].r){
         a[ll].val=a[rr].val=a[root].val;
         a[root].val=-;
     }
 }

 void update(int l,int r,int val,int root){
     if(a[root].val==val) return;
     if(a[root].l==l&&a[root].r==r){
         a[root].val=val;
         return;
     }
     down(root);
     if(r<=a[ll].r) update(l,r,val,ll);
     else if(l>=a[rr].l) update(l,r,val,rr);
     else{
         update(l,mid,val,ll);
         update(mid+,r,val,rr);
     }
     if(a[ll].val==a[rr].val&&a[ll].val>) a[root].val=a[ll].val;
 }

 bool visited[N];
 int ans;

 void query(int root){
     if(a[root].val!=-&&!visited[a[root].val]) {
         ans++;
         visited[a[root].val]=true;
         return;
     }
     if(a[root].l==a[root].r)return ;
     down(root);
     query(ll);
     query(rr);
 }

 void out(int root){
     if(a[root].l==a[root].r) {
         printf("%d ",a[root].val);
         return;
     }
     down(root);
     out(ll);
     out(rr);
 }

 main()
 {
     int t, i, j, k;

     cin>>t;
     while(t--){
         scanf("%d",&n);
         k=;
         for(i=;i<n;i++) {
             scanf("%d %d",&line[i].l,&line[i].r);
             x[++k]=line[i].l;
             x[++k]=line[i].r;
         }
         sort(x+,x+k);
         k=unique(x+,x+k+)-x;
         m=k;
         for(i=;i<k;i++){
             if(x[i]-x[i-]>) x[m++]=x[i]-;
         }
         sort(x,x+m);
         build(,m,);
         for(i=;i<n;i++){
             int l=bin_s(line[i].l);
             int r=bin_s(line[i].r);
             update(l,r,i+,);

         }
         memset(visited,false,sizeof(visited));
         ans=;
         query();
         printf("%d\n",ans);
         //out(1);
     }
 }