lintcode:买卖股票的最佳时机 I

买卖股票的最佳时机

假设有一个数组，它的第i个元素是一支给定的股票在第i天的价格。如果你最多只允许完成一次交易(例如,一次买卖股票),设计一个算法来找出最大利润。

样例

给出一个数组样例 [3,2,3,1,2], 返回 1

解题

法一：直接暴力，时间发杂度O(N²)

public class Solution {
    /**
     * @param prices: Given an integer array
     * @return: Maximum profit
     */
    public int maxProfit(int[] prices) {
        // write your code here
        int Max = 0;
        if( prices == null || prices.length == 0)
            return 0;

        for(int i = 0;i< prices.length ;i++){
            for(int j = i;j< prices.length ;j++)
                Max = Math.max(Max, prices[j] - prices[i]);
        }
        return Max;
    }
}

法二：动态规划，选取最小的卖，最大的买，利润最大。

public class Solution {
    /**
     * @param prices: Given an integer array
     * @return: Maximum profit
     */
    public int maxProfit(int[] prices) {
        // write your code here
        int result = 0;
        if( prices == null || prices.length == 0)
            return 0;
        int minbuy = prices[0];
        for(int i = 1;i< prices.length ;i++){
            // 最小的购买，最大的卖
            result = Math.max(result,prices[i] - minbuy);
            minbuy = Math.min(minbuy,prices[i]);
        }
        return result;
    }
}

时间复杂度O(N)

Python

class Solution:
    """
    @param prices: Given an integer array
    @return: Maximum profit
    """
    def maxProfit(self, prices):
        # write your code here
        if prices == None or len(prices) ==0:
            return 0
        Min = prices[0]
        res = 0
        for p in prices:
            res = max(res,p-Min)
            Min = min(Min,p)
        return res 

法三：分治法

参考《算法导论》

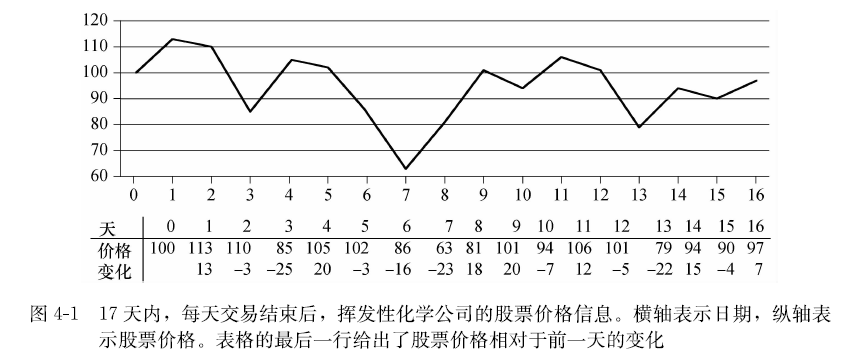
题目要求的是一次购买，一次卖出使得所获价格变化最大。可以考虑每一天的价格变化，第i天的价格变化 等于第i天的价格减去i-1天的价格，这样就会有许多价格变化的数据形成的数组，求这个数组的连续子数组的和的最大值就是答案了。为什么这个这个最大连续子数组就是答案？

假设原始数组是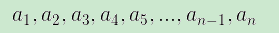：，若最大收益是 an - a1

相邻差数组是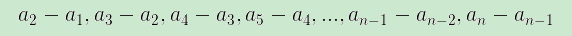：,显然这个的连续和也是an - a1

问题转化为求最大连续子数组

对上图的例子：

分治法求解最大子数组

假定我们要寻找子数组A[low,...,high]的最大子数组。使用分治法意味着我们要将子数组分成两个规模尽量相同的子数组。也就是说，找到子数组的中央位置，比如：mid,然后考虑求两个子数组A[low,...,mid] 和A[mid+1,...,high]。

A[low,...,high]的然后连续子数组A[i,...,j]所处的位置必然是一下三种情况之一：

（1）完全位于子数组A[low,...,mid]中，因此low<=i<=j<=mid

（2）完全位于子数组A[mid+1,...,high]中，因此mid+1<=i<=j<=high

（3）跨越了中间点，因此low<=i<=mid<=j<=high

所以，可以递归的求解（1）（2）两种情况的最大子数组，剩下的就是对（3）情况寻找跨越中间点的最大子数组，然后在三种情况中选取和最大者。如下图所示

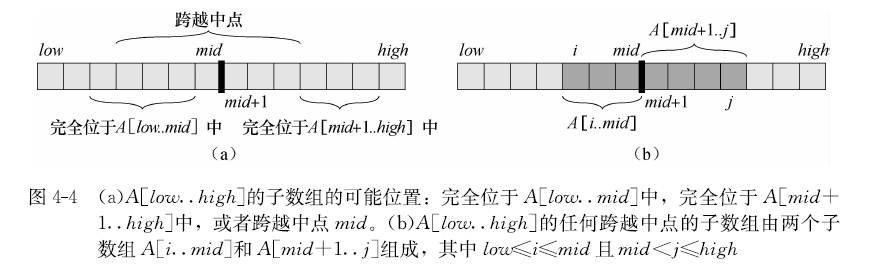
对于跨越中间点的最大子数组，可以在线性时间内求解。可以找出A[i,...,mid] 和A[mid+1,...,j]的最大子数组，合并就是答案。

参考算法导论写的寻找经过中间点时候的最大连续子数组

    public int findMaxCrossingSubarray(int[] A,int low,int mid,int high){
        if(low > mid || mid>high)
            return Integer.MIN_VALUE;
        int leftSum = Integer.MIN_VALUE;
        int rightSum = Integer.MIN_VALUE;
        int sum = 0;
        int maxleft = -1;
        int maxright = -1;
        for(int i = mid;i>=low;i--){
            sum+=A[i];
            if( sum >= leftSum){// 向左只要和增加就更新
                leftSum = sum;
                maxleft = i;
            }
        }
        sum = 0;
        for(int j = mid+1;j<=high;j++){
            sum+=A[j];
            if(sum>=rightSum){
                rightSum = sum;
                maxright = j;
            }
        }
        return leftSum + rightSum;
    }

算法导论上的伪代码

时间复杂度O(N)

上面有返回的边界，我只是返回了子数组的最大值

下面在递归的求解整个数组的最大连续子数组

    public int findMaxSubarray(int[] A,int low,int high){
        if(low == high)
            return Math.max(A[low],0);
        else{
            int mid = low + (high - low)/2;// 防止越界
            int leftSum = findMaxSubarray(A,low,mid);//(1)
            int rightSum = findMaxSubarray(A,mid+1,high);//(2)
            int midSum = findMaxCrossingSubarray(A,low,mid,high);//(3)
            int sum = Math.max(leftSum,rightSum);
            sum = Math.max(sum,midSum);
            sum = Math.max(sum,0);
            return sum;
        }
    }

上面标的（1）（ 2）（ 3）对应上面分析的（1）（2）（3）

上面代码中最后的结果和0求了最大值，lintcode测试用例可以不买不卖的情况，由于买了一定会亏，就不买了的情况，题目要求最大一次交易，就是可以不交易的了。

算法导论上的伪代码

时间复杂度分析：

递归情况：

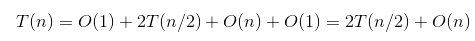 这个等式很显然的

当n=1的时候就是O(1)

所以：

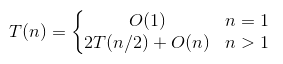
时间复杂度是：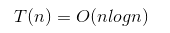

具体时间复杂度求解参考《算法导论》

对于求解最大子数组，当然也可以运用动态规划求解

全部程序

public class Solution {
    /**
     * @param prices: Given an integer array
     * @return: Maximum profit
     */
    public int maxProfit(int[] prices) {
        // write your code here
        if(prices == null || prices.length == 0)
            return 0;
        int[] A = new int[prices.length - 1];
        for(int i = 1;i<prices.length ;i++)
            A[i-1] = prices[i] - prices[i-1];
        int maxSubarray = findMaxSubarray(A,0,A.length - 1);
        return maxSubarray;
    }
    public int findMaxSubarray(int[] A,int low,int high){
        if(low == high)
            return Math.max(A[low],0);
        else{
            int mid = low + (high - low)/2;// 防止越界
            int leftSum = findMaxSubarray(A,low,mid);//(1)
            int rightSum = findMaxSubarray(A,mid+1,high);//(2)
            int midSum = findMaxCrossingSubarray(A,low,mid,high);//(3)
            int sum = Math.max(leftSum,rightSum);
            sum = Math.max(sum,midSum);
            sum = Math.max(sum,0);
            return sum;
        }
    }
    public int findMaxCrossingSubarray(int[] A,int low,int mid,int high){
        if(low > mid || mid>high)
            return Integer.MIN_VALUE;
        int leftSum = Integer.MIN_VALUE;
        int rightSum = Integer.MIN_VALUE;
        int sum = 0;
        int maxleft = -1;
        int maxright = -1;
        for(int i = mid;i>=low;i--){
            sum+=A[i];
            if( sum >= leftSum){// 向左只要和增加就更新
                leftSum = sum;
                maxleft = i;
            }
        }
        sum = 0;
        for(int j = mid+1;j<=high;j++){
            sum+=A[j];
            if(sum>=rightSum){
                rightSum = sum;
                maxright = j;
            }
        }
        return leftSum + rightSum;
    }
}