矩阵的QR分解（三种方法）Python实现

1.Gram-Schmidt正交化

假设原来的矩阵为[a,b]，a,b为线性无关的二维向量，下面我们通过Gram-Schmidt正交化使得矩阵A为标准正交矩阵：

假设正交化后的矩阵为Q=[A,B],我们可以令A=a，那么我们的目的根据AB=I来求B，B可以表示为b向量与b向量在a上的投影的误差向量：

$$B=b-Pb=b-\frac{A^Tb}{A^TA}A$$

 

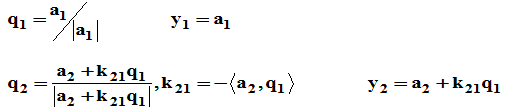
2.Givens矩阵与Givens变换

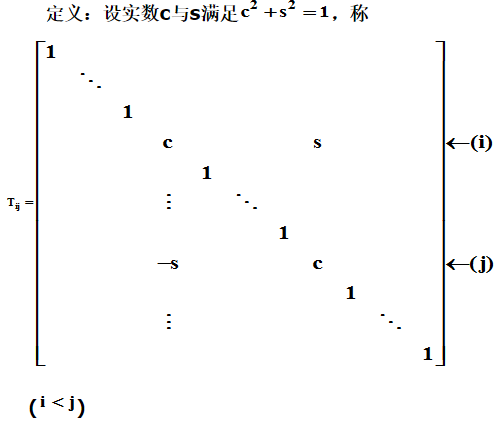
为Givens矩阵（初等旋转矩阵），也记作。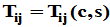

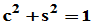由Givens矩阵所确定的线性变换称为Givens变换（初等旋转变换）。

实数，故存在，使。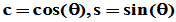

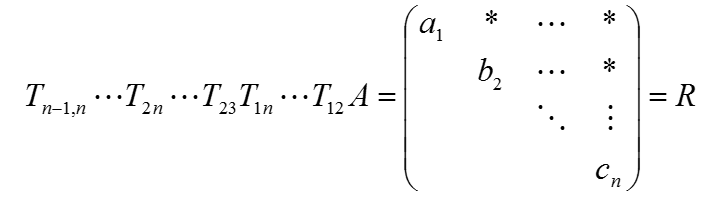
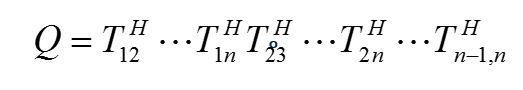
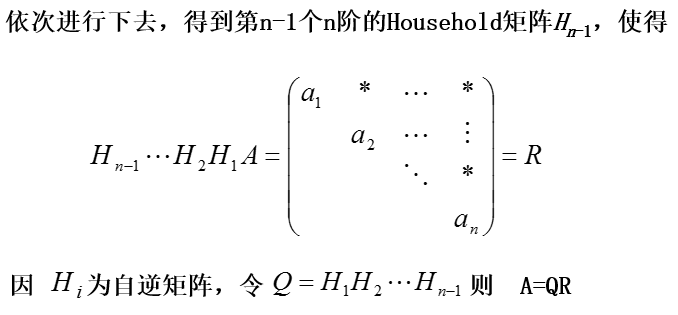
3.Householder矩阵与Householder变换

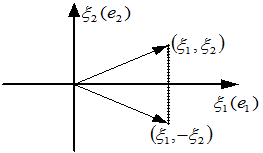
平面直角坐标系中，将向量关于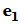轴作为交换，则得到

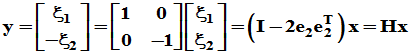
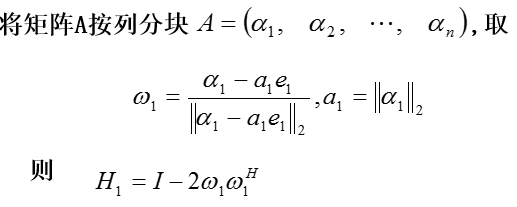
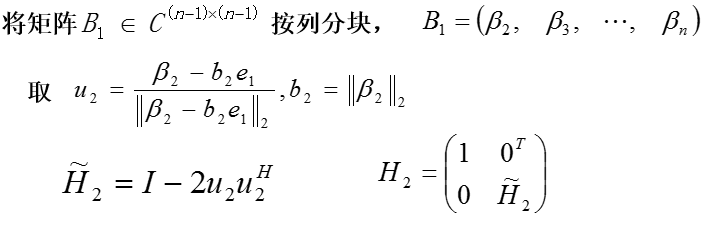
 #coding:utf8
 import numpy as np

 def gram_schmidt(A):
     """Gram-schmidt正交化"""
     Q=np.zeros_like(A)
     cnt = 0
     for a in A.T:
         u = np.copy(a)
         for i in range(0, cnt):
             u -= np.dot(np.dot(Q[:, i].T, a), Q[:, i]) # 减去待求向量在以求向量上的投影
         e = u / np.linalg.norm(u)  # 归一化
         Q[:, cnt] = e
         cnt += 1
     R = np.dot(Q.T, A)
     return (Q, R)

 def givens_rotation(A):
     """Givens变换"""
     (r, c) = np.shape(A)
     Q = np.identity(r)
     R = np.copy(A)
     (rows, cols) = np.tril_indices(r, -1, c)
     for (row, col) in zip(rows, cols):
         if R[row, col] != 0:  # R[row, col]=0则c=1,s=0,R、Q不变
             r_ = np.hypot(R[col, col], R[row, col])  # d
             c = R[col, col]/r_
             s = -R[row, col]/r_
             G = np.identity(r)
             G[[col, row], [col, row]] = c
             G[row, col] = s
             G[col, row] = -s
             R = np.dot(G, R)  # R=G(n-1,n)*...*G(2n)*...*G(23,1n)*...*G(12)*A
             Q = np.dot(Q, G.T)  # Q=G(n-1,n).T*...*G(2n).T*...*G(23,1n).T*...*G(12).T
     return (Q, R)

 def householder_reflection(A):
     """Householder变换"""
     (r, c) = np.shape(A)
     Q = np.identity(r)
     R = np.copy(A)
     for cnt in range(r - 1):
         x = R[cnt:, cnt]
         e = np.zeros_like(x)
         e[0] = np.linalg.norm(x)
         u = x - e
         v = u / np.linalg.norm(u)
         Q_cnt = np.identity(r)
         Q_cnt[cnt:, cnt:] -= 2.0 * np.outer(v, v)
         R = np.dot(Q_cnt, R)  # R=H(n-1)*...*H(2)*H(1)*A
         Q = np.dot(Q, Q_cnt)  # Q=H(n-1)*...*H(2)*H(1)  H为自逆矩阵
     return (Q, R)

 np.set_printoptions(precision=4, suppress=True)
 A = np.array([[6, 5, 0],[5, -1, 4],[5, 1, -14],[0, 4, 3]],dtype=float)

 (Q, R) = gram_schmidt(A)
 print(Q)
 print(R)
 print np.dot(Q,R)

 (Q, R) = givens_rotation(A)
 print(Q)
 print(R)
 print np.dot(Q,R)

 (Q, R) = householder_reflection(A)
 print(Q)
 print(R)
 print np.dot(Q,R)