2021.8.18 NKOJ周赛总结

两个字总结：安详

T1: NKOJ-6179 NP问题

问题描述：

p6pou在平面上画了n个点，并提出了一个问题，称为N-Points问题，简称NP问题。

p6pou首先在建立的平面直角坐标系，并标出了这n个点的坐标。这n个点的坐标都是正整数，任意三个点都不共线。
然后，p6pou选择其中一个点A，画一条y轴的平行线，这条直线称为l。
直线l以A点为旋转中心逆时针旋转，当直线l碰到另外一个点B时，就立刻将B点作为新的旋转中心继续逆时针旋转。
此后，每当直线l碰到除了旋转中心以外的另一个点，都会将这个点作为新的旋转中心继续逆时针旋转。这个过程可以一直进行。

p6pou不太关心旋转的完整过程，只想知道，当l旋转至平行于x轴时直线方程有哪些可能。

输入格式：

第一行输入两个整数n,A，表示平面上共有n个点，一开始l与y轴平行，直线方程是x=A。

第2到第n+1行中，第i+1行两个正整数xi,yi，表示编号为i的点的坐标，保证任意三点不共线。

输出格式：

直线l旋转到与x轴平行时方程是y=B，按从小到大的顺序输出B所有可能的值，每行输出一个数。

数据范围：

对于10%的数据，n=3；
对于10%的数据，n=4；
对于30%的数据，n≤10；
对于50%的数据，n≤50；
对于另外20%的数据，A=min{x1,x2,...,xn}；
对于100%的数据， 3≤n≤200,1≤xi,yi,A≤106,A∈{x1,x2,…,xn} 。

样例输入：

6 2
2 2
2 4
4 1
4 2
3 4
1 3

样例输出：

2
3
4

样例解释：

初始旋转中心可以是第1个点或者第2个点。如果初始旋转中心是第1个点，旋转过程平行于x轴有y=2和y=4两种情况；如果初始旋转中心是第2个点，旋转过程平行于x轴有y=2和y=3两种情况 （详见下图）

　　一道所谓的签（不）到题。

　

　　很毒瘤。先讲讲这道题的来源：ta本来是道数竞题，原题要求证明 “ 一定存在直线 l 使得每一个点都能成为旋转中心 ”，当然证明是数竞的事，这里就不证了，读者自证不难（主要是没听懂）。

　　

　　一看这道题，肯定首先会想到模拟，但这个实在太复杂了，斜率、atan() 似乎不好做，而且好像会TML。那怎么办呢？

　　仔细观察上图，可以发现：当直线 l 从一定转移到另一点时，直线 l 两侧点数之差不变。　这就是解题的关键所在。

　　既然两侧点数之差不变，那我们可以先求出开始直线 l 两侧点数之差，在枚举每一个点，若当前点可以使直线 l 与 y轴 平行，那么直线 l 两侧点数之差于初始时相同。

　　但要注意线上有两点的情况，线上两点可以选一个做为中心，另一个可以随意加入任意一侧。

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n,K,P,Del,head,Ans[205];
struct node {int x,y;}A[205];
#define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++)
char buf[65536],*p1,*p2;
inline int read()
{
    char ch;int x(0);
    while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
int main()
{
    n=read(),K=read();
    for(register int i=1;i<=n;++i)
    {
        A[i].x=read(),A[i].y=read();
        if(A[i].x==K) ++P;
        else if(A[i].x<K) ++Del;
        else --Del;
    }
    Del=abs(Del);
    for(register int i=1;i<=n;++i)
    {
        int p(0),del(0);
        for(register int j=1;j<=n;++j)
        {
            if(A[j].y==A[i].y) ++p;
            else if(A[j].y>A[i].y) ++del;
            else --del;
        }
        del=abs(del);
        if(Del==del||((P==2||p==2)&&abs(Del-del)==1)||(P==2&&p==2&&abs(Del-del)<=2)) Ans[++head]=A[i].y;
    }
    sort(Ans+1,Ans+head+1);
    for(register int i=1;i<=head;++i) if(Ans[i]!=Ans[i-1]) printf("%d\n",Ans[i]);
    return 0;
}

NP问题

（NP问题都解决了，还坐这干嘛）

---

T2: NKOJ-8440 多叉树转二叉树

问题描述：

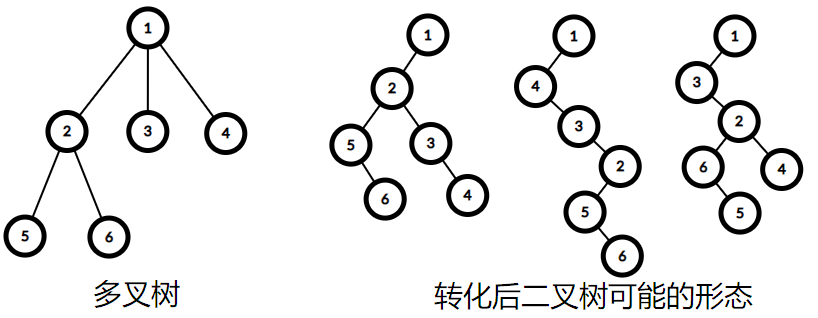
一棵有根树，规定根节点深度为 0 ，其他节点深度等于父亲的深度 +1 。

有一棵多叉树，你需要把它按照“左儿子右兄弟”的规则转化为二叉树。例如下图左边的多叉树，转化后的二叉树可以是右边的几种情况。

设节点 x 转化前后深度分别为 d1[x],d2[x] ，则转化的代价为
∑x∣∣d1[x]−d2[x]∣∣

请你分别求出最小代价和最大代价。

输入格式：

第一行一个整数 n 。节点编号 1∼n ，其中 1 号节点是根。

接下来 n 行，每行两个数 xi,yi ，表示多叉树的一条边。

输出格式：

输出两个整数，表示转化的最小代价和最大代价。

数据范围：

对于 20% 的数据， n≤10 ；
对于 30% 的数据， n≤20 ；
对于 40% 的数据， n≤200 ；
对于 60% 的数据， n≤5000 ；
对于 100% 的数据， 1≤n≤500000 。

　　这才是真正的签到题。

　　显然，对于一个点 x , ta的子树越大，越往下放，贡献越大。

　　将儿子按子树大小排序，从小到大DFS即为最大值，从大到小DFS即为最小值。

Code:

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n,Deep[500005],Size[500005],Cnt,Head[500005],Next[1000005],To[1000005];
long long Ans[2];
struct node {int p,Size;}Tmp[500005];
bool cmp1(node a,node b) {return a.Size<b.Size;}
bool cmp2(node a,node b) {return a.Size>b.Size;}
#define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++)
char buf[65536],*p1,*p2;
inline int read()
{
    char ch;int x(0);
    while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y;}
inline void DFS1(int x,int fa)
{
    Deep[x]=Deep[fa]+1,Size[x]=1;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];if(j==fa) continue;
        DFS1(j,x),Size[x]+=Size[j];
    }
}
inline void DFS2(int x,int fa,int deep)
{
    int head(0);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];if(j==fa) continue;
        Tmp[++head].p=j,Tmp[head].Size=Size[j];
    }
    sort(Tmp+1,Tmp+head+1,cmp1);int Temp[head+5];
    for(register int i=1;i<=head;++i) Temp[i]=Tmp[i].p;
    for(register int i=1,j;i<=head;++i) j=Temp[i],Ans[1]+=abs(Deep[j]-deep-i),DFS2(j,x,deep+i);

}
inline void DFS3(int x,int fa,int deep)
{
    int head(0);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];if(j==fa) continue;
        Tmp[++head].p=j,Tmp[head].Size=Size[j];
    }
    sort(Tmp+1,Tmp+head+1,cmp2);int Temp[head+5];
    for(register int i=1;i<=head;++i) Temp[i]=Tmp[i].p;
    for(register int i=1,j;i<=head;++i) j=Temp[i],Ans[0]+=abs(Deep[j]-deep-i),DFS3(j,x,deep+i);
}
int main()
{
    n=read(),Deep[0]=-1;
    for(register int i=1,x,y;i<n;++i) x=read(),y=read(),ADD(x,y),ADD(y,x);
    DFS1(1,0),DFS2(1,0,0),DFS3(1,0,0),printf("%lld %lld",Ans[0],Ans[1]);
    return 0;
}

多叉树转二叉树

---

T3：NKOJ-8441 最长公共子序列

问题描述：

对一棵有根树执行一次DFS，可以得到一个前序遍历和一个后序遍历，设它们的最长公共子序列长度和方案数分别是 f,g 。
DFS时可以任意调整子树顺序，不同顺序的DFS会得到不同的前序和后序遍历。
设最长公共子序列长度的最大值是 F ，方案总数是 G 。
即 F=max所有DFS顺序(f) ， G=∑所有DFS顺序(g) 。

给你一棵无根树，请你求出将每个节点 u 被设为根时的 Fu,Gu 。 
Gu 可能很大所以 mod998,244,353 。

输入格式：

第一行一个整数 n 。树上节点编号 1∼n 。

接下来 n−1 行，每行两个整数 xi,yi 表示树上一条边。

输出格式：

输出 n 行，每行两个整数，即 Fu 和 Gumod998,244,353 。

数据范围：

对于 20% 的数据， n≤10 ；
对于 30% 的数据， n≤100 ；
对于 40% 的数据， n≤5000 ；
对于另外 30% 的数据， n≤500000 ，保证节点 2∼n 的度数都 ≤2 ；
对于 100% 的数据， n≤500000 。

　　对于以 x 为根的树（如下图，其中 a , b , c 代表以其为根的子树）

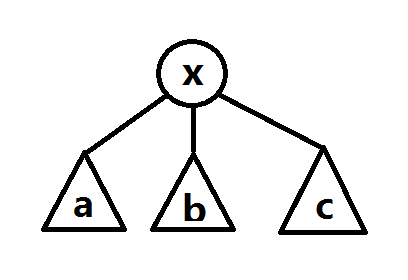
　　ta的前序遍历是： x , a , b , c ；后序遍历是： a , b , c , x 。

　　我们可以得出结论：一棵有根树的最长公共子序列长度为其叶子节点个数。

　　那么，F 就解决了，只需要求出叶子节点个数，再记一下它是不是叶子。

　　然后来讨论 G ：

　　　　对于上图，不难发现：对于一个红圈而言，任选一个点并不会影响答案，将它命名为“叶链”，即从叶子开始，到第一个度数为3的点之前为止；

　　　　对一个非叶链上的点 a ，其答案为：∏（In [ x ] - 1 ) !  ∏ ( Size [ y ] ) * In [ a ] （其中，x为非叶链上点，y为叶链上点，In [ ] 为度数，Size [ ] 为叶链大小）；

　　　　对一个叶链上的点 a ，其答案为：∏（In [ x ] - 1 ) !  ∏ ( Size [ y ] ) * Len [ a ] / Size [ a ] * In [ a ] （其中，x为非叶链上点，y为叶链上点，In [ ] 为度数，Len [ ] 为点到叶子距离，Size [ ] 为叶链大小）；

　　　　由于前面有大量重复项，可以把  ∏（In [ x ] - 1 ) !  ∏ ( Size [ y ] )  提出来计算。

　　但要注意，n == 1 和 图为一条链 的情况要特判一下

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define mod 998244353
using namespace std;
bool flag;
int n,In[500005],Cnt,Head[500005],Next[1000005],To[1000005],Len[500005],Size[500005],Ans1[500005];
long long Fac[500005],Com(1),Ans2[500005];
#define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++)
char buf[65536],*p1,*p2;
inline int read()
{
    char ch;int x(0);
    while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y;}
inline void Inv(int x) {Fac[0]=1;for(register int i=1;i<=x;++i) Fac[i]=Fac[i-1]*i%mod;}
inline void DFST(int x,int fa)
{
    Ans1[x]=Ans1[fa]+1;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];if(j==fa) continue;
        DFST(j,x);
    }
}
inline void DFS1(int x,int fa)
{
    Len[x]=Len[fa]+1,Size[x]=Size[fa]+1;
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];if(j==fa||In[j]>2) continue;
        DFS1(j,x),Size[x]=Size[j];
    }
}
inline long long Mon(long long x)
{
    int RET(1),b(998244351);
    while(b>0)
    {
        if(b%2==1) RET=(RET*x)%mod;
        b>>=1,x=(x*x)%mod;
    }
    return RET;
}
int main()
{
    n=read();
    if(n==1) {printf("1 1");return 0;}
    for(register int i=1,x,y;i<n;++i)
    {
        x=read(),y=read(),ADD(x,y),ADD(y,x),++In[x],++In[y];
        if(In[x]>2||In[y]>2) flag=1;
    }
    if(!flag)
    {
        for(register int i=1;i<=n;++i)
            if(In[i]==1) {DFST(i,0);break;}
        for(register int i=1;i<=n;++i)
            if(In[i]==1) printf("1 %d\n",n);
            else printf("2 %lld\n",2LL*(Ans1[i]-1)%mod*(n-Ans1[i])%mod);
        return 0;
    }
    Inv(n);
    for(register int i=1;i<=n;++i)
        if(In[i]==1) DFS1(i,0),++Ans1[0],--Ans1[i],Com=Com*Size[i]%mod;
        else Com=Com*Fac[In[i]-1]%mod;
    for(register int i=1;i<=n;++i)
        if(!Len[i]) Ans2[i]=Com*In[i]%mod;
        else if(Len[i]!=1) Ans2[i]=Com*(Len[i]-1)%mod*Mon(Size[i])%mod*2%mod;
        else Ans2[i]=Com*Mon(Size[i])%mod;

    for(register int i=1;i<=n;++i) printf("%d %lld\n",Ans1[0]+Ans1[i],Ans2[i]);
    return 0;
}

最长公共子序列

---

T4：NKOJ-8442 最小生成树

问题描述：

三维空间中给定 n 个点，在任意两点之间连一条边的代价为它们的曼哈顿距离，求最小生成树。

输入格式：

第一行一个整数 n 。

接下来 n 行，每行三个整数 xi,yi,zi ，表示一个点的坐标。

输出格式：

一个整数，表示最小生成树的所有边的代价之和。

数据范围：

对于 20% 的数据， n≤5000 ；
对于另外 30% 的数据， n≤50000 ， zi=0 ；
对于另外 30% 的数据， n≤50000 ，保证坐标在 [−108,108] 范围内均匀随机；
对于 100% 的数据， 1≤n≤50000 ，坐标范围 [−108,108] 。

（待更，预计更新时间：Eons）