Machine learning(3-Linear Algebra Review )
1、Matrices and vectors
- Matrix :Rectangular array of numbers
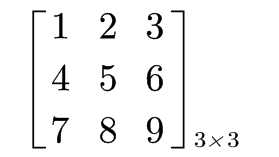
a notation R3×3
- Vector : An n×1 matrix
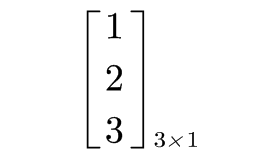
this is a three dimensional vector , a notation R3
2、Addition and scalar multiplication
3、Matrix-vector multiplication
内标相同即可乘,前行×后列得一行 (可运用Python直接计算,参考用python检查矩阵的计算)



4、Matrix-matrix multiplication
- Same as above
5、Matrix multiplication properties
- No commutative A×B ≠ B×A (B is not identity matrix)
- Yes associative (A×B)×C=A×(B×C)

- For any matrix A, A×I = I×A = A
6、Inverse and transpose
- Inverse :
we can use python to implement and for example :
from numpy import *# 自行判断|A|≠0# 求逆矩阵 ,建议:取小数点后一位化为分数A = mat([[1, -1, 1],[1, 1, 0],[-1, 0, 1]])B = A.Iprint(B)# [ 0.33333333 0.33333333 -0.33333333]# [-0.33333333 0.66666667 0.33333333]# [ 0.33333333 0.33333333 0.66666667]# 0.333≈ 1/3 ,0.667≈ 2/3
- Transpose :
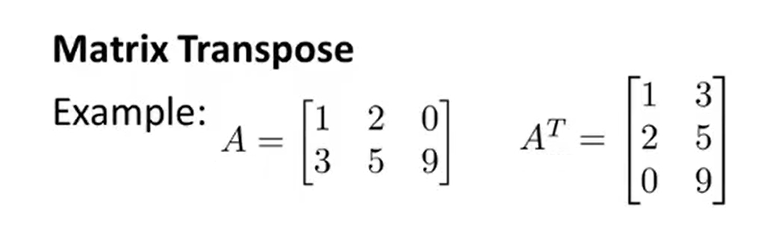
Machine learning(3-Linear Algebra Review )的更多相关文章
- 机器学习---最小二乘线性回归模型的5个基本假设(Machine Learning Least Squares Linear Regression Assumptions)
在之前的文章<机器学习---线性回归(Machine Learning Linear Regression)>中说到,使用最小二乘回归模型需要满足一些假设条件.但是这些假设条件却往往是人们 ...
- Codeforces 940F Machine Learning (带修改莫队)
题目链接 Codeforces Round #466 (Div. 2) Problem F 题意 给定一列数和若干个询问,每一次询问要求集合$\left\{c_{0}, c_{1}, c_{2}, ...
- CF940F Machine Learning(带修莫队)
首先显然应该把数组离散化,然后发现是个带修莫队裸题,但是求mex比较讨厌,怎么办?其实可以这样求:记录每个数出现的次数,以及出现次数的出现次数.至于求mex,直接暴力扫最小的出现次数的出现次数为0的正 ...
- Fast and accurate bacterial species identification in urine specimens using LC-MS/MS mass spectrometry and machine learning (解读人:闫克强)
文献名:Fast and accurate bacterial species identification in urine specimens using LC-MS/MS mass spectr ...
- 机器学习---用python实现最小二乘线性回归算法并用随机梯度下降法求解 (Machine Learning Least Squares Linear Regression Application SGD)
在<机器学习---线性回归(Machine Learning Linear Regression)>一文中,我们主要介绍了最小二乘线性回归算法以及简单地介绍了梯度下降法.现在,让我们来实践 ...
- 算法库:基础线性代数子程序库(Basic Linear Algebra Subprograms,BLAS)介绍
调试DeepFlow光流算法,由于作者给出的算法是基于Linux系统的,所以要在Windows上运行,不得不做大量的修改工作.移植到Windows平台,除了一些头文件找不到外,还有一些函数也找不到.这 ...
- Pattern Recognition and Machine Learning (preface translation)
前言 鉴于机器学习产生自计算机科学,模式识别却起源于工程学.然而,这些活动能被看做同一个领域的两个方面,并且他们同时在这过去的十年间经历了本质上的发展.特别是,当图像模型已经作为一个用来描述和应用概率 ...
- Targeted Learning R Packages for Causal Inference and Machine Learning(转)
Targeted learning methods build machine-learning-based estimators of parameters defined as features ...
- Machine learning(1-Introduction)
1.What is machine learning Field of study that gives computers the ability to learn without being ex ...
- A brief introduction to weakly supervised learning(简要介绍弱监督学习)
by 南大周志华 摘要 监督学习技术通过学习大量训练数据来构建预测模型,其中每个训练样本都有其对应的真值输出.尽管现有的技术已经取得了巨大的成功,但值得注意的是,由于数据标注过程的高成本,很多任务很难 ...
随机推荐
- vue-cli 项目中使用 v-chart 及导出 chart 图片
安装: npm i v-charts echarts -S 组件中使用: 1 <template> 2 <div class="app-chart"> 3 ...
- 机器学习——逻辑回归(Logistic Regression)
1 前言 虽然该机器学习算法名字里面有"回归",但是它其实是个分类算法.取名逻辑回归主要是因为是从线性回归转变而来的. logistic回归,又叫对数几率回归. 2 回归模型 2. ...
- dede织梦会员模板调用template下模板head.htm方法及解析变量
1.找到dedecms会员中心的的目录 member ,然后在目录下用编辑器打开config.php 加入对dede模板解释函数如下: //php脚本开始 //引入arc.partview.cla ...
- Java基础系列(39)- 二维数组
多维数组 多维数组可以看成是数组的数组,比如二维数组就是一个特殊的一维数组,其每一个元素都是一个一维数组. 二维数组 int a[][]=new int[2][5]; 解析:以上二维数组a可以看成一个 ...
- sonar-scanner的使用
在服务器搭建sonarqube后,本地的windows个人电脑如何使用sonar-scanner? 在服务器搭建sonarqube后,每个人都可以在本地使用sonar-scanner扫描代码. son ...
- Python简单算法的实现
#coding=utf-8 #!/usr/bin/python def GCD(a,b): """ :求两个数的最大公约数 :param a: :param b: :re ...
- P6113-[模板]一般图最大匹配【带花树】
正题 题目链接:https://www.luogu.com.cn/problem/P6113 题目大意 给出一张无向图,求最大匹配. \(1\leq n\leq 10^3,1\leq m\leq 5\ ...
- YbtOJ#643-机器决斗【贪心,李超树】
正题 题目链接:https://www.ybtoj.com.cn/problem/643 题目大意 \(n\)个机器人,第\(i\)个攻击力为\(A_i\),防御为\(D_i\). 然后你每次可以对一 ...
- 深入浅出WPF-02.WPF系列目录
WPF系列目录 2. XAML认识 3. XAML语法 4. x名称空间详解 5. 控件与布局 6. 绑定Binding-01 6. 绑定Binding-02 6. 绑定Binding-03 7. 属 ...
- 关于Windows操作系统重定向
在用C++做一个文件遍历的时候发现,当我遍历C:\Windows\system32文件夹时,获取到的文件数目和实际总是对不上.在通过他人帮助后了解到了重定向这个概念,我百度了一下,下面为粘贴内容. S ...




