Tarjan算法离线 求 LCA（最近公共祖先）

本文是网络资料整理或部分转载或部分原创，参考文章如下：

https://www.cnblogs.com/JVxie/p/4854719.html

http://blog.csdn.net/ywcpig/article/details/52336496

https://baike.baidu.com/item/最近公共祖先/8918834?fr=aladdin

最近公共祖先，简称LCA（Lowest Common Ancestor）：

所谓LCA：是当给定一个有根树T时，对于任意两个结点u、v，找到一个离根最远的结点x，使得x同时是u和v的祖先，x 便是u、v的最近公共祖先。

再通俗地解释一下：在一棵没有环的树上，每个节点肯定有其父亲节点和祖先节点，而最近公共祖先，就是两个节点在这棵树上深度最大的公共的祖先节点。换句话说，就是两个点在这棵树上距离最近的公共祖先节点。所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。LCA还可以将自己视为祖先节点。

本文为了简化，多使用二叉树来讨论。

举个例子，如针对下图所示的一棵普通的二叉树来讲：

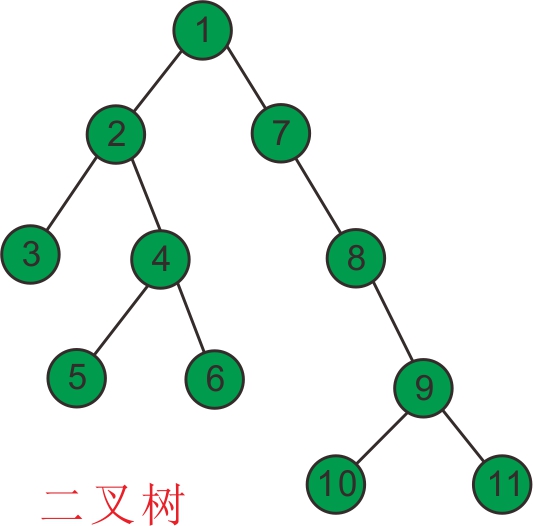
结点3和结点4的最近公共祖先是结点2，即LCA（3，4）=2 。

需要注意到当两个结点在同一棵子树上的情况。

如结点3和结点2的最近公共祖先为2，即 LCA（3，2）=2。

同理：LCA（5，6）=4，LCA（6，10）=1。

明确了题意，咱们便来试着解决这个问题。直观的做法，可能是针对是否为二叉查找树分情况讨论，这也是一般人最先想到的思路。除此之外，还有Tarjan算法、倍增算法、以及转换为RMQ问题（求某段区间的极值）。

我们先来讲讲暴力解法：

如果是二叉查找树，如下图：

那么从树根开始：

• 如果当前结点t 大于结点u、v，说明u、v都在t 的左侧，所以它们的共同祖先必定在t 的左子树中，故从t 的左子树中继续查找；

• 如果当前结点t 小于结点u、v，说明u、v都在t 的右侧，所以它们的共同祖先必定在t 的右子树中，故从t 的右子树中继续查找；

• 如果当前结点t 满足 u <t < v，说明u和v分居在t 的两侧，故当前结点t 即为最近公共祖先；

• 而如果u是v的祖先，那么u就是最近公共祖先，同理，如果v是u的祖先，那么v就是最近公共祖先。

伪代码如下所示：

int query(Node t, Node u, Node v) {    
    int left = u.value;    
    int right = v.value;    
 
   //二叉查找树内，如果左结点大于右结点，就交换。不知道为什么要交换  
    if (left > right) {    
        int temp = left;    
        left = right;    
        right = temp;    
    }    
 
    while (true) {    
        //如果t小于u、v，往t的右子树中查找  
        if (t.value < left) {    
            t = t.right;    
        //如果t大于u、v，往t的左子树中查找  
        } else if (t.value > right) {    
            t = t.left;    
        } else {    
            return t.value;    
        }    
    }    
}

如果不是二叉查找树，对于每个询问，就暴力遍历所有的点，时间复杂度为O(n*q)，q是询问的次数。很明显，n和q一般不会很小。此处略......

然后我们再来讲一讲如何用Tarjan算法离线解决LCA：

离线算法就是指统一输入后再统一输出，而不是边输入边实时输出。Tarjan算法的复杂度为O（N+Q），Q为询问的次数。相当于一次性批量处理，一开始就知道了全部查询，只待询问。

下面详细介绍一下Tarjan算法的基本思路：看不明白没关系，我们后面会模拟的。

　　1.任选一个点为根节点，从根节点开始。

　　2.遍历该点u所有子节点v，并标记这些子节点v已被访问过。

　　3.若是v还有子节点，返回第2步，否则下一步。

　　4.合并v到u上。

　　5.寻找与当前点u有询问关系的点v。

6.若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。

遍历的话需要用到dfs来遍历，至于合并，最优化的方式就是利用并查集来合并两个节点。

下面上伪代码： 

我们先来直接模拟一下用Tarjan来解决LCA，然后再总结。

 

假设我们有一组数据 9个节点 8条边 联通情况如下：

1--2，1--3，2--4，2--5，3--6，5--7，5--8，7--9 即下图所示的树

设我们要查找最近公共祖先的点为9和8，4和6，7和5，5和3；

设f[]数组为并查集的父亲节点数组，初始化f[i]=i，vis[]数组为是否访问过的数组，初始为0;

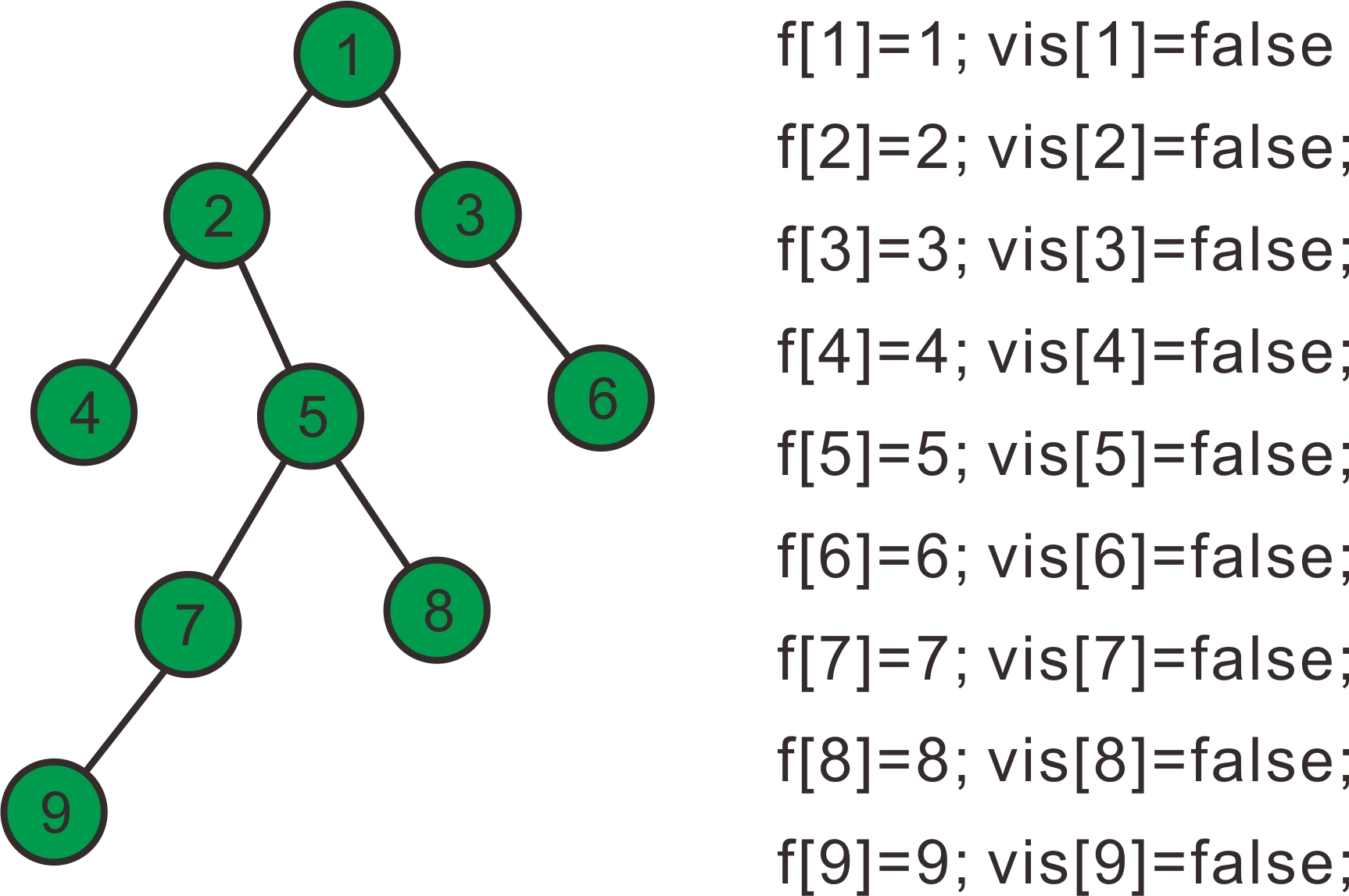
下面开始模拟过程：

　取1为根节点，往下搜索发现有两个儿子2和3；

　先搜2，发现2有两个儿子4和5，先搜索4，发现4没有子节点，则寻找与其有关系的点；

　发现6与4有关系，但是vis[6]=false，即6还没被搜过，所以不操作；

　发现没有和4有询问关系的点了，返回此前一次搜索，更新vis[4]=true，表示4已经被搜完，再更新f[4]=2，表示4被合并到2，如下图： 

　　　　

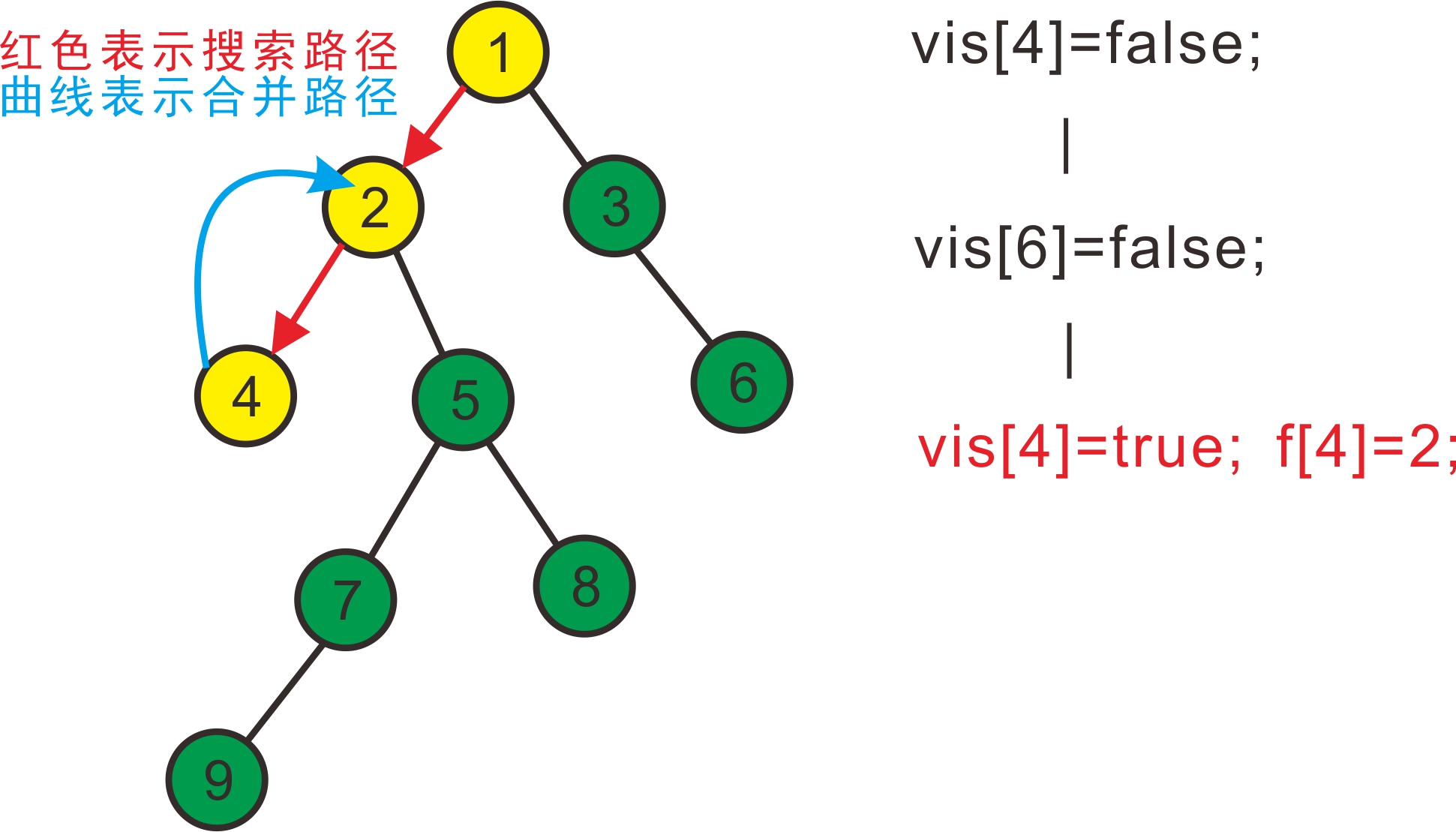
　继续搜5，发现5有两个儿子7和8;

　先搜7，发现7有一个子节点9，搜索9，发现没有子节点，寻找与其有关系的点；

发现8和9有关系，但是vis[8]=false,即8没被搜到过，所以不操作；

　发现没有和9有询问关系的点了，返回此前一次搜索，更新vis[9]=true；

　表示9已经被搜完，更新f[9]=7；

回到7，发现7没有没被搜过的子节点了，寻找与其有关系的点；

　发现5和7有关系，但是vis[5]=false，所以不操作；

　发现没有和7有关系的点了，返回此前一次搜索，更新vis[7]=true；　　　　

　表示7已经被搜完，更新f[7]=5。如下图：

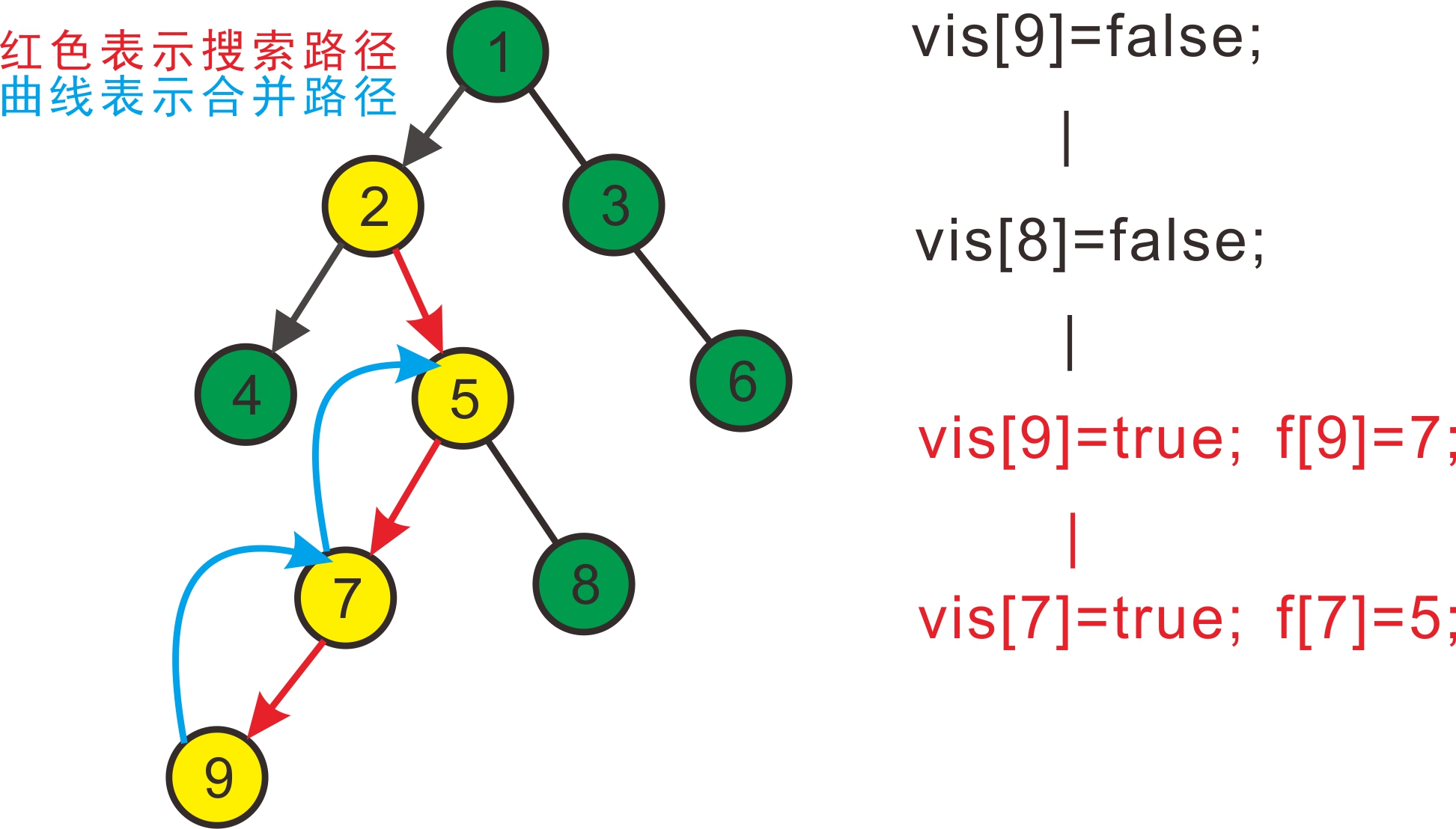
继续搜8，发现8没有子节点，则寻找与其有关系的点；

发现9与8有关系，此时vis[9]=true，则他们的最近公共祖先为find(9)=5；（此处好好想一想）

find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5; 

发现没有与8有关系的点了，返回此前一次搜索，更新vis[8]=true；

表示8已经被搜完，更新f[8]=5。如下图：

　　　　

回到5发现5也没有没搜过的子节点了，寻找与其有关系的点；

发现7和5有关系，此时vis[7]=true，所以他们的最近公共祖先为find(7)=5；

find(7)的顺序为f[7]=5-->f[5]=5 return 5;

又发现5和3有关系，但是vis[3]=false，所以不操作，此时5的子节点全部搜完了；

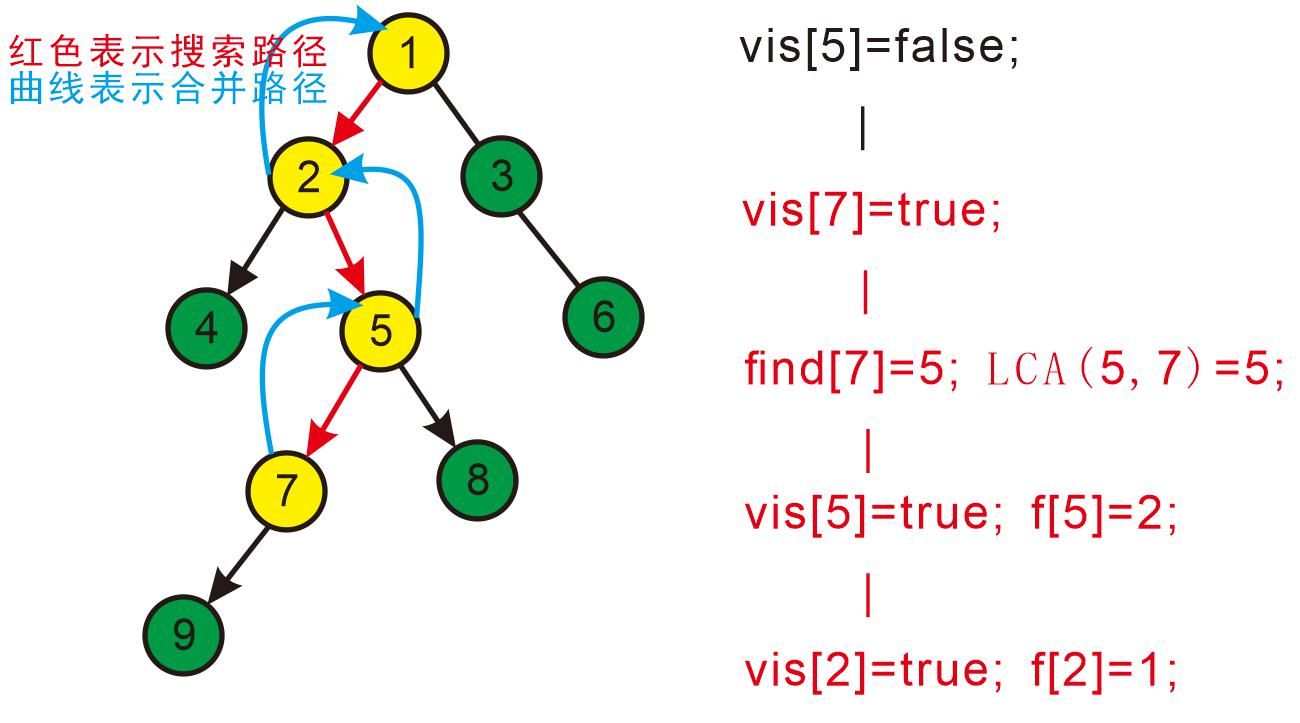
返回此前一次搜索，更新vis[5]=true，表示5已经被搜完，更新f[5]=2；

回到2发现2没有未被搜完的子节点，寻找与其有关系的点；

发现没有和2有关系的点，返回此前一次搜索，更新vis[2]=true；　　　　

表示2已经被搜完，更新f[2]=1。如下图：

接着搜3，发现3有一个子节点6；

搜索6，发现6没有子节点，则寻找与6有关系的点，发现4和6有关系；

此时vis[4]=true，所以它们的最近公共祖先为find(4)=1;

find(4)的顺序为f[4]=2-->f[2]=1-->f[1]=1 return 1;

发现没有与6有关系的点了，返回此前一次搜索，更新vis[6]=true，表示6已经被搜完了；

更新f[6]=3。如下图：

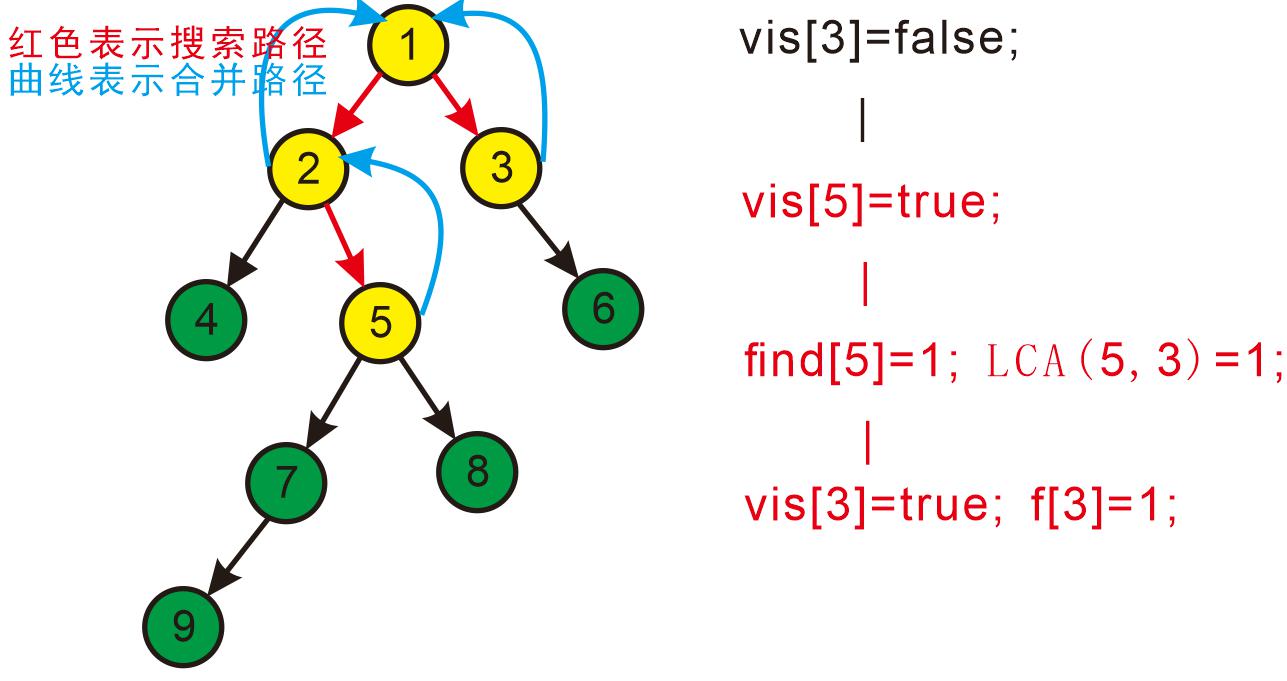
回到3发现3没有没被搜过的子节点了，则寻找与3有关系的点；

发现5和3有关系，此时vis[5]=true，则它们的最近公共祖先为find(5)=1；

find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1; 

发现没有和3有关系的点了，返回此前一次搜索，更新vis[3]=true；更新f[3]=1。

如下图：

最后发现1没有被搜过的子节点也没有有关系的点，此时可以退出整个dfs了。

经过这次dfs我们得出了所有的答案。

总结：

Tarjan离线算法，将所求先储存，然后结合并查集和DFS，

如果所求的两个点都vis[]==1，那么输出他们的father

除了求LCA外，Tarjan算法也可以用来求有向图的强连通分量，具体请参考我的另一篇博文。

P3379 【模板】最近公共祖先（LCA）

https://www.luogu.org/problemnew/show/3379

2370 小机房的树

http://codevs.cn/problem/2370/

1036 商务旅行

http://codevs.cn/problem/1036/

LCA  Tarjan算法模板   参考代码C++

https://www.cnblogs.com/fish7/p/4006056.html

http://blog.csdn.net/qq_24451605/article/details/43114243

http://blog.csdn.net/mzyupengju/article/details/47146789

http://blog.csdn.net/tekim/article/details/77750093

https://www.cnblogs.com/jsawz/p/6723221.html