spring切面-单线程简单权限判定

spring切面简单模拟用户权限判定

需求：

游客：仅注册用户

用户：修改，注册

管理员：删除，查询，修改，注册

1，文件配置

导包

src下创建applicationContext.xml文件配置如下

2，程序设计思路

2.1：controller-->service-- >dao-->模拟注册，查询，修改，删除

2.2：由测试携带权限-->controller-->切面判断权限-->service-->dao-->模拟注册，查询，修改，删除

3，程序难点在于切面判断方法，本程序采用：注解标注 携带枚举类型权限值 在切面进行权限判断

4，缺点：仅支持单线程

目录结构：

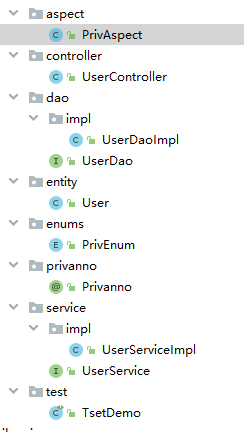
实体类：User

枚举：创建权限 ，cust游客 user用户，admin管理员

注解：用来标记方法的权限

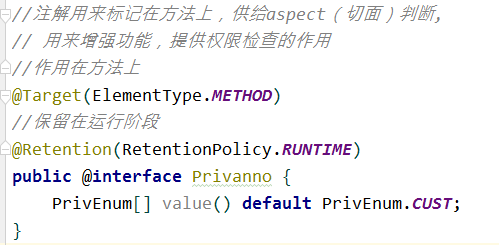
测试类：模拟携带权限执行方法

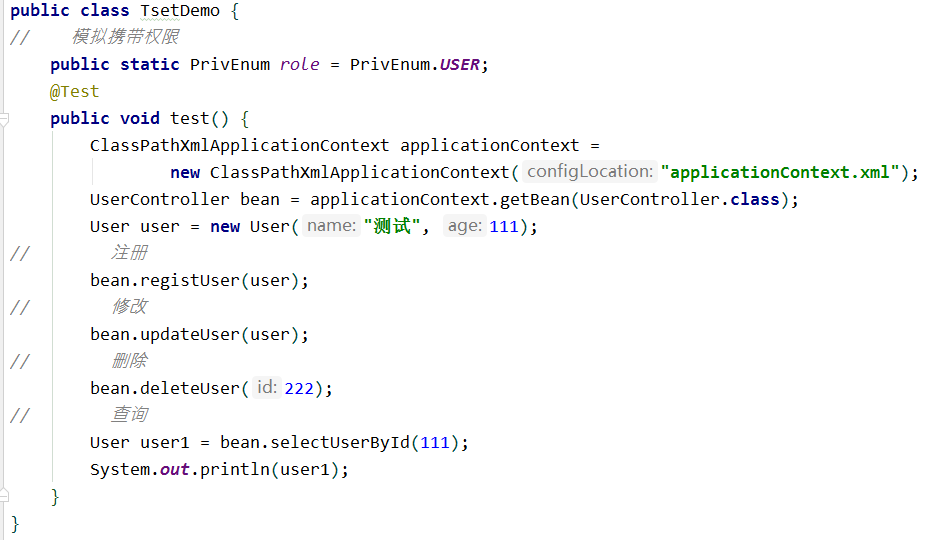
controller层：调用service层形成连接点，通过切入点表达式筛选切入点

aspect切面：利用环绕通知来实现权限判断

注意点：一定要通过目标对象去获取方法名上的注解携带值

而不是signature.getMethod()获取到的接口方法名

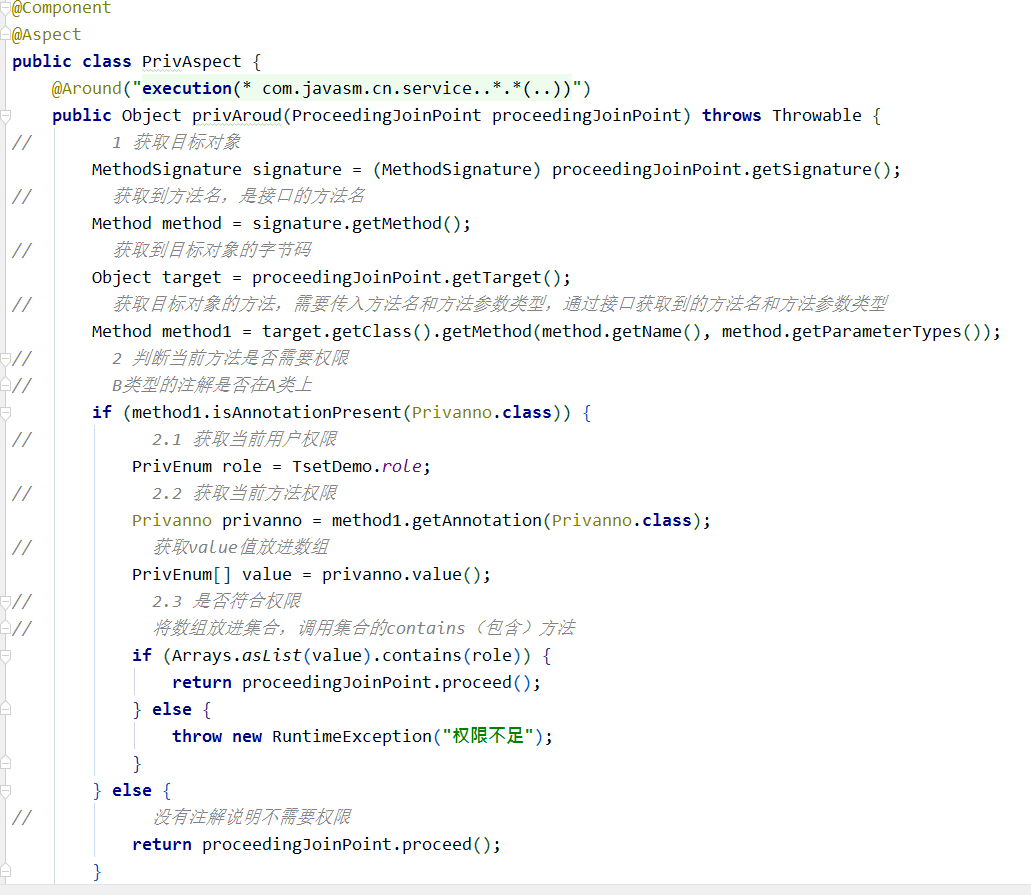
service层实现类：携带注解权限，调用dao层

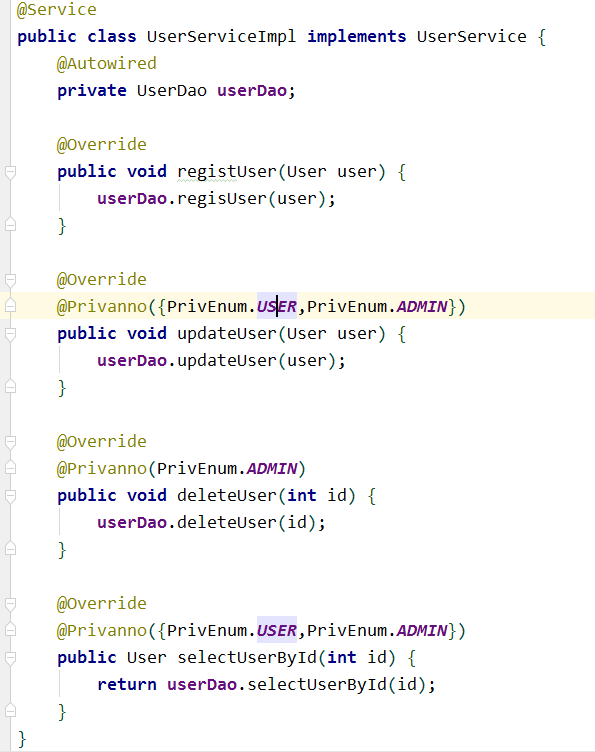
dao层实现类：用注解携带权限值  仅模拟，不做真实数据操作

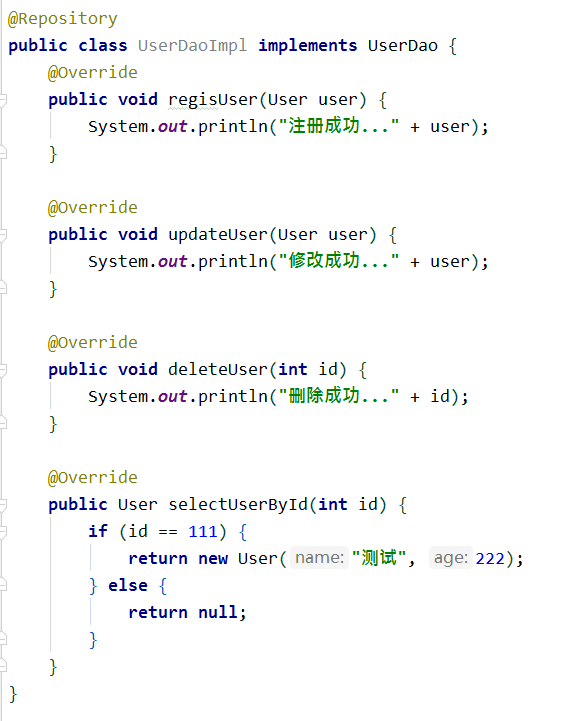
User权限结果如下：