【LeetCode】62. Unique Paths 解题报告(Python & C++)

作者： 负雪明烛
id： fuxuemingzhu
个人博客： http://fuxuemingzhu.cn/

---

题目地址：https://leetcode.com/problems/unique-paths/description/

题目描述：

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

题目大意

给出了一个m * n的地图，上面有个机器人位于左上角，现在他想到达右下角。它每次只能向右边或者下边走一步，问能到达右下角的方式有多少种。

解题方法

方法一：组合公式

这个题搞明白之后其实就是一个排列组合中的组合类型的题目。

在总数为m + n - 2中的数目中挑选n - 1个位置放竖着的走。也就是我们说的C(m + n - 2)(n -1)的问题。

组合公式的计算方式为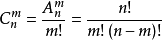：，使用公式计算出结果就行了。

时间复杂度是O(m + n)，空间复杂度是O(1)。

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        total = m + n - 2
        v = n - 1
        def permutation(m, n):
            son = 1
            for i in range(m, m - n, -1):
                son *= i
            mom = 1
            for i in range(n, 0, -1):
                mom *= i
            return son / mom
        return permutation(total, min(v, total -v))

方法二：记忆化搜索

到达某个位置的次数怎么计算？可以想到是到达这个位置上面的位置的次数+到达坐标的次数。这里需要说明的是因为两个这个机器人走的方向只能向右或者向下，所以它到达上边位置和左边位置的次数中没有交集，所以可以直接相加。

把问题分解之后，我们就想到了用递归，那么递归的终止条件是什么？明显地机器人到达第一行或者第一列任意位置的可能性方式只有一种！那就是一直向这个方向走！

另外使用了记忆化数组保存已经走过位置的次数，可以加快运算。

时间复杂度是O(m * n)，空间复杂度是O(m * n)。超过了99%的提交。

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        memo = [[0] * n for _ in range(m)]
        return self.dfs(m - 1, n - 1, memo)

    def dfs(self, m, n, memo):
        if m == 0 or n == 0:
            return 1
        if memo[m][n]:
            return memo[m][n]
        up = self.dfs(m - 1, n, memo)
        left = self.dfs(m, n - 1, memo)
        memo[m][n] = up + left
        return memo[m][n]

方法三：动态规划

看到上面记忆化搜索的方法就知道这个题同样可以使用动态规划解决。第一行第一列的所有方式只有1种，到达其他位置的方式是这个位置上面 + 这个位置左边用DP的话，和上面记忆化搜索差不多。

时间复杂度是O(m * n)，空间复杂度是O(m * n)。超过了17%的提交，没有上面搜索快。

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        dp = [[0] * n for _ in range(m)]
        for i in range(m):
            dp[i][0] = 1
        for i in range(n):
            dp[0][i] = 1
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i][j - 1] + dp[i - 1][j]
        return dp[m - 1][n - 1]

上面是把dp初始化为0，也可以换初始化为1：

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        dp = [[1] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if i == 0 or j == 0:
                    continue
                dp[i][j] = dp[i][j - 1] + dp[i - 1][j]
        return dp[m - 1][n - 1]

使用C++代码如下，这次是把所有的位置都初始化成0，除了机器人刚开始所在的位置[1,1]设置成了1.

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        dp[1][1] = 1;
        for (int i = 1; i < m + 1; ++i) {
            for (int j = 1; j < n + 1; ++j) {
                if (i == 1 && j == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m][n];
    }
};

日期

2018 年 2 月 19 日
2018 年 10 月 18 日
2018 年 12 月 29 日 —— 2018年剩余电量不足1%