PSP初体验：求交点

项目	内容
课程：北航2020春软件工程	博客园班级博客
作业：完成一个平面图形求交点的程序，体验PSP的过程	个人项目作业
我在这个课程的目标是	体验软件开发的全流程
这个作业在哪个具体方面帮助我实现目标	体会PSP的过程
教学班级	006
项目地址	https://github.com/lzhmarkk/lineCross

时间规划

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	2	5
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	180	200
· Design Spec	· 生成设计文档	20	15
· Design Review	· 设计复审 (和同事审核设计文档)	3	1
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	NaN	2
· Design	· 具体设计	15	10
· Coding	· 具体编码	30	100
· Code Review	· 代码复审	10	5
· Test	· 测试（自我测试，修改代码，提交修改）	30	240
Reporting	报告
· Test Report	· 测试报告	10	30
· Size Measurement	· 计算工作量	5	5
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	5	5
	合计	310	618

需求分析

本次作业需要做一个计算平面直角坐标系中直线于直线之间交点的程序。

那么就浮现出以下几个问题：

• 如何表示点：

  封装一个类，包含\(x\)和\(y\)两个属性

• 如何去表示直线：

  \(y=kx+b\)似乎面对平行于y轴的直线有点无力，采用\(ax+by+c=0\)的形式

  封装一个类，包含\(a\)，\(b\)，\(c\)三个属性

• 如何去表示圆：

  \((x-m)^2+(y-n)^2=r^2\)

  封装一个类，包含\(m\)，\(n\)，\(r\)三个属性

• 直线和直线的交点如何求：

  直线联立解方程，给出预先解好的结果，直接代入求解

  \(x=\frac{b_1*c_2-b_2*c_1}{a_1*b_2-a_2*b_1}\)，\(y=\frac{a_2*c_1-a_1*c_2}{a_1*b_2-a_2*b_1}\)

• 直线与圆的交点如何求：

  • 若直线不平行于y轴：

    联立解方程，可以得到\(ix^2+jx+k=0\)，其中\(i=a^2+b^2\)，\(j=2ac+2nab-2mb^2\)，\(k=(m^2+n^2-r^2)b^2+c^2-2nbc\)

    再考虑解\(ix^2+jx+k=0\)这个方程得到交点的x值，回代直线方程得到交点坐标

  • 若直线平行于y轴：

    判断半径与圆心到直线的距离关系，若半径更大，说明有交点，交点纵坐标可通过已知的横坐标代入圆方程解出；若半径更小，说明无交点

• 圆和圆的交点如何求：

  两圆方程相减，得到公共弦方程或者公共切点的公切线方程或者两圆重心所在直线。再用该直线与其中任一圆相交，可得到交点。

• 特殊情况有哪些

  • 点重合

    根据样例3，这种情况只算一个点

  • 直线平行但不重合

    意识到不可以直接带入上述公式，需要作出判断

  • 直线重合

    有无数解，但是题目规定题目输入保证答案只有有限个，故暂不考虑，编码时可以考虑使用assert

  • 圆重合

    有无数解，但是题目规定题目输入保证答案只有有限个，故暂不考虑，编码时可以考虑使用assert

• 其他问题

  • 没用过C++

    预计花费一小时学习和摸索语法和特殊用法

  • 没用过Visual Studio，而且linux系统上没有VS

    预计花费两个小时熟悉IDE的编辑、调试和项目管理，以及性能测试等功能

设计

我设计了以下几个类和一个函数：

//Graph.h
class Dot {};//用于表示一个点

class Graph {};//接口，便于扩展圆

class Line : public Graph {};//用于表示一条线，采用ax+by+c=0表示

class Circle : public Graph {};//用于表示一个圆，采用(x-m)^2+(y-n)^2=r^2来表示

/*  用于计算图像和图像之间的交点
	params: Graph *a, Graph *b
	return: 图a和图b的交点列表
*/
vector<Dot> solve(Graph *a, Graph *b);

class Container {};//用于存储交点，并除去重合的点

其中solve函数逻辑如下：

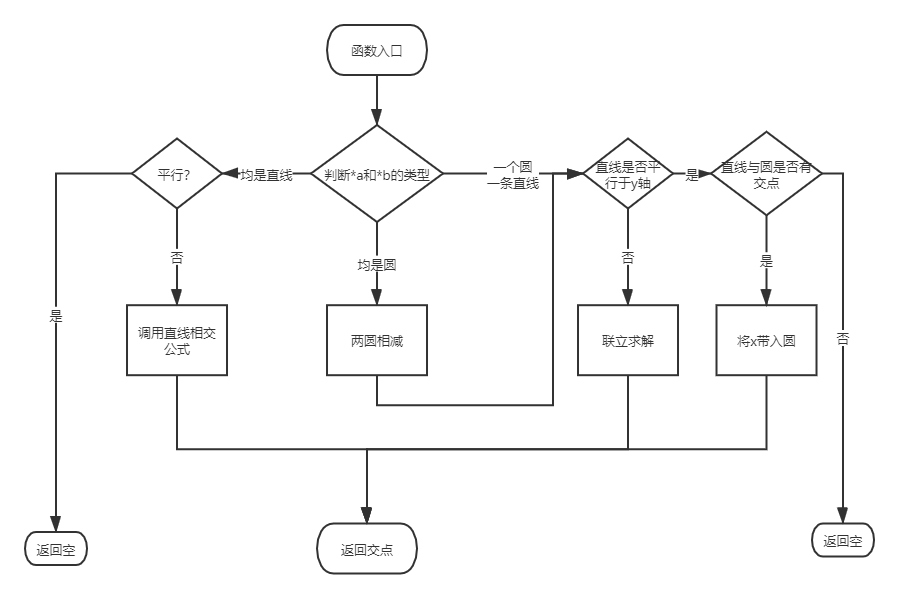
测试

• 测试Dot类，其中包括了以下几个方面：

  • 构造函数

  • equals()方法测试，尤其是double类型存在着极小的误差

    使用const double eps = 1e-6作修正，若\(|a-b|<eps\)则视为\(a==b\)

• 测试Line类，其中包括以下几个方面：

  • 两种构造函数的测试（通过点构造和直接通过abc的值构造）
  • 斜率（如果存在的话）值的计算和截距（如果存在的话）值的计算

• 测试Circle类，其中包括以下几个方面：

  • 构造函数的测试

• 测试solve方法，其中输入为以下几种情况：

  • 线与线
    • 平行
    • 重合
    • 不平行
  • 圆圆
    • 相离
    • 相交
    • 内切
    • 外切
    • 内含
    • 同心
    • 重合
  • 线圆
    • 线垂直于x轴
    • 线垂直于y轴
    • 线不垂直于x或y轴

• 测试Container模块，主要是对相同（两者各自坐标差在eps范围之内的）的点能否做到不重

对每一种情况，我都设计一组数据对其进行测试。

性能优化

刚开始我的Container是采用vector来实现，每次得到一个点的时候都需要检查之前处理过的所有点以检查重复性，同时担心double类型的误差，我均要利用eps来减小误差，导致其时间非常长

后来将Container改写成了set的结构，使得其效率得到极大的提升

以下是VS给出的性能分析图

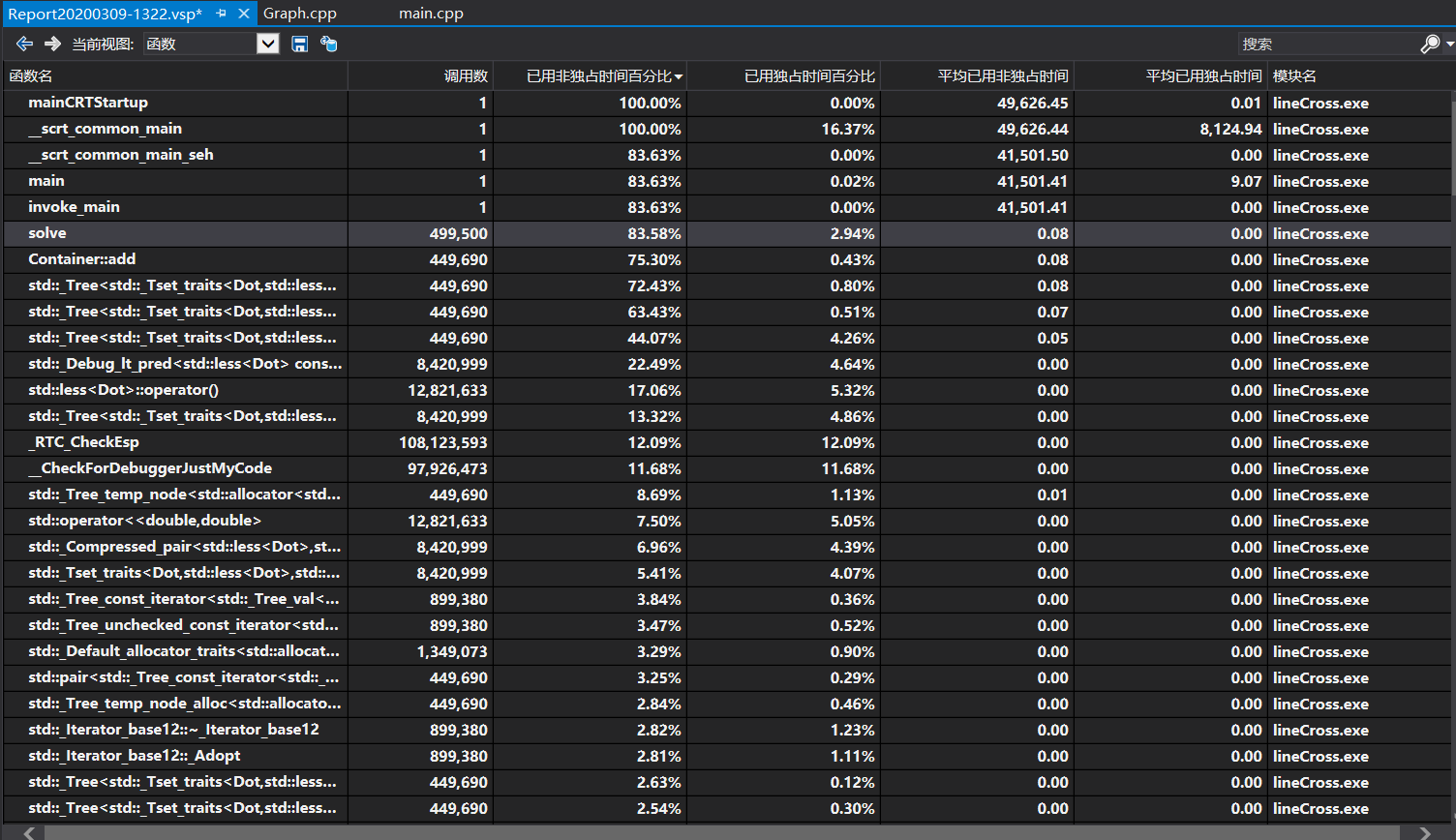
图中可以看出，构建RB树的时间占用最多，其中最大一部分就是std::less<Dot>::operator()也就是比较两个结点之间的时间

再后来我取消了esp的考虑，因为发现利用RB树来构建set的话，其中有以下几个原因：

• 比较两个结点所占的时间超过了总程序运行时间的80%，取消eps效率提升接近一倍
• 出现\(10^{-7}\)以下误差的概率比较低，在直线相交的情况下几乎不可能出现

代码风格

采用的是“Microsoft建议”的风格。

关键代码

由于源代码相对较长，这里给出伪代码

void solve(Container *con, Graph* g1, Graph* g2){
	if (aIsLine && bIsLine) {
		//if both is line
		if (!parrallel){
			double x = (b1 * c2 - b2 * c1) / (a1 * b2 - a2 * b1);
			double y = (a2 * c1 - a1 * c2) / (a1 * b2 - a2 * b1);
			con->add(Dot(x, y));
		}
	} else if (aIsLine && !bIsLine) {
		//if g1 is line and g2 is circle
		if (g1 is vertical) {
			double distance = pow(_r, 2) - pow(x - _m, 2);
			if (distance >= 0) {
				calculateY();//垂径定理求y
				con->add(Dot(x1, y1));
				con->add(Dot(x2, y2));
			}
		} else {
		euqationX = equation(g1, g2);//联立直线和圆，消去y
		solveEquation(euqationX);//解关于x的方程
		con->add(Dot(x1, y1));
		con->add(Dot(x2, y2));
		}
	} else if (!aIsLine && bIsLine) {
		//if g1 is circle and g2 is line
		return solve(con, g2, g1);
	} else {
		//if both are circle
		Line* l = g2 - g1;
		return solve(con, l, g2);
	}
}

因为采用了非常非常暴力的方法来联立求解线和圆、圆和圆的交点，所以在计算上相对缓慢而且可能会造成double类型的误差的累积。

但是笔者也承认其中存在着bug，那就是在处理圆的时候double的精度问题几乎没有修正，最终结果基本只有小数点后的前6位是可信的，那么在判断点和点是否重合的时候，必然会造成误差和错误。