BUAA_OO_第一单元

BUAA_OO_2020_UNIT1

一、程序结构分析

• 第一次作业

  UML & Mertrics

  

  

​ 由于数据处理简单，第一次作业中笔者发挥了面向过程的思想，将项转换成Biginteger, Biginteger的字典逐项输出就行了，导致类复杂度、方法复杂度耦合度都很高，后面只能重写。笔者在后面作业意识到这种面向过程式程序不利于迭代开发。

• 第二次作业

  UML & Mertrics

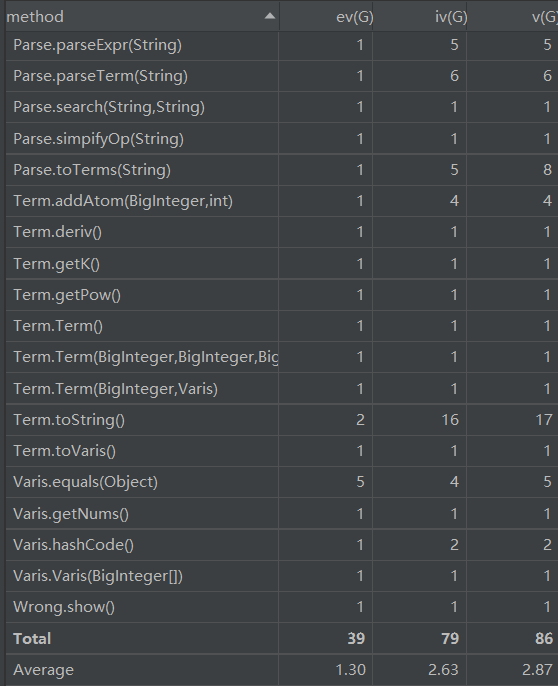
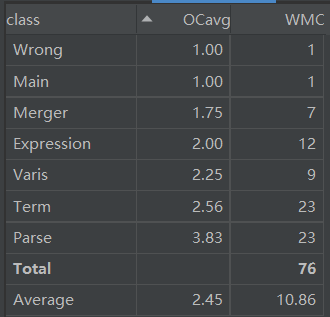
​ 笔者在第二次作业中建立了项-表达式的层次，建立了合并类与输入处理类，但没有将因子也建立类，导致第三次作业无法处理嵌套再次重构，Parse类与项Term类较臃肿，因为笔者将四元组作为项的数据结构。

• 第三次作业

  UML & Mertrics

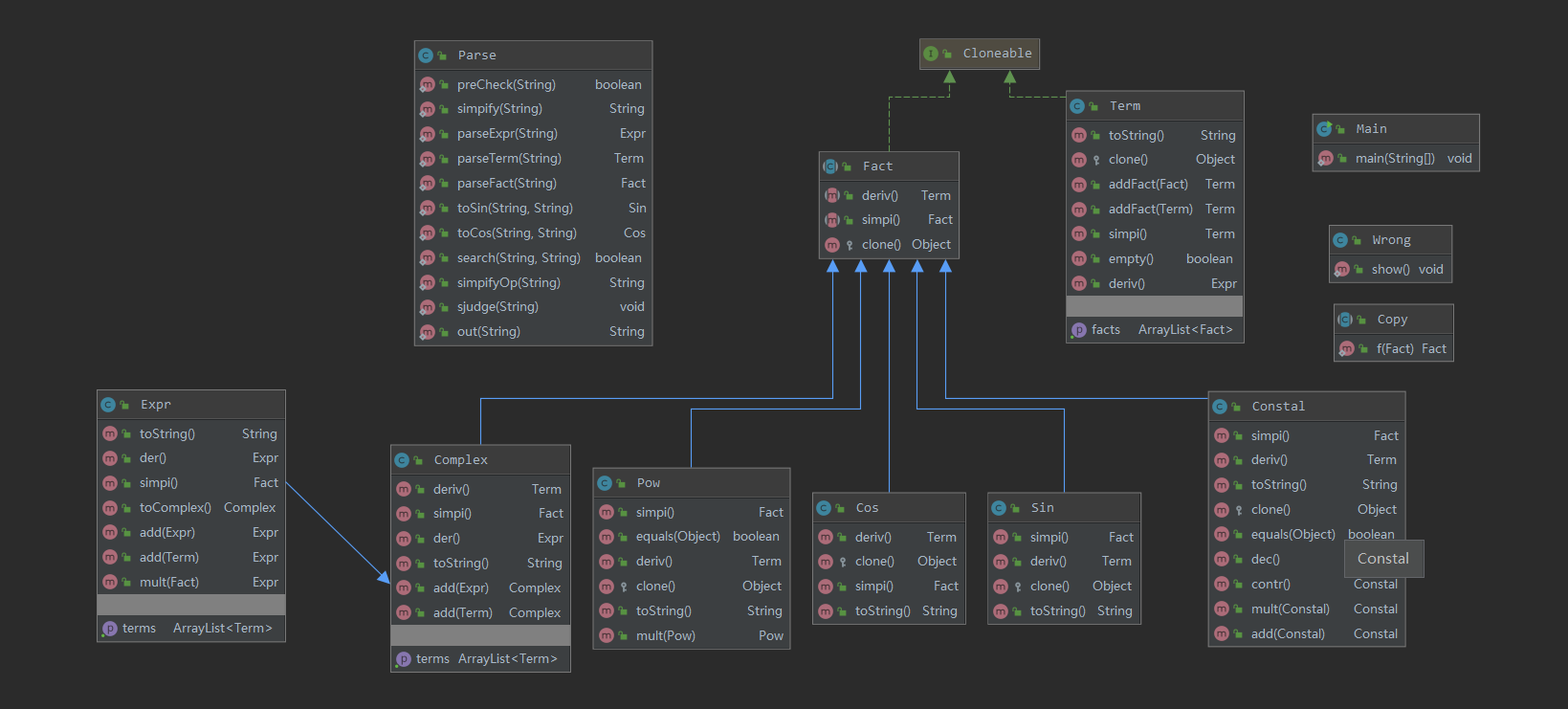
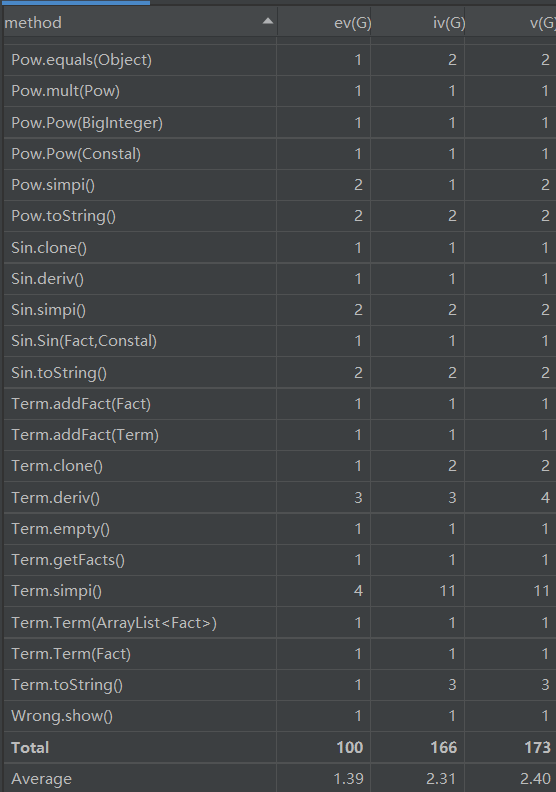
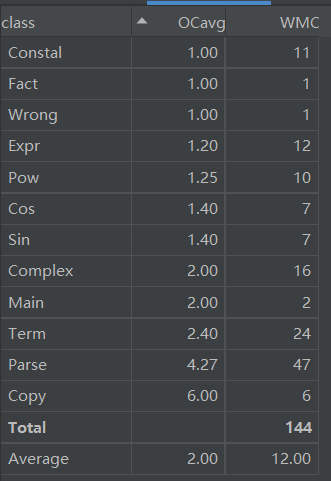
​ 笔者在第三次作业根据表达式-项-因子的层次建立类，Term类与Parse类仍然复杂，因为笔者在此次作业中，把输入输出处理聚集在Parse，把化简方法分散到Term，Fact类中，导致耦合度较高。

二、Bug分析

• 笔者两处Bug都在输出化简上
  • 第二次作业中，笔者没有在正常数Term前打印'+'，因为Term输出函数内if-else太多了，也很难看，笔者随后想到打印Term时正项一定打印'+'，并优先输出常数的方法，对于表达式Expr中多符号直接换成单符号，"+1*"直接换成"+"就完事了，然而，
  • 第三次作业中，笔者逻辑错误，对于Term，先合并Term中的因子Fact，再把Term中实例为复合因子Complex且只含一个Term的拆成ArrayList<Fact>加入Term中；显然这两次处理顺序反了，于是可能输出一个以上连续的常数因子Constal（+5*+1*....），超出了笔者的设想，化简方法于是造成了错误。

三、互测策略

• 仔细看别人的代码，我从一些结构清晰的同学的代码收获很多，对于结构混乱没有注释的还是放弃阅读吧

• 一个一个运行其他人Project太慢了，可以写程序输入一组数据然后让其他人程序同时运行得到多人的输出，提高效率

• 构造边界数据，可惜这次不能输入非法数据

四、对象创建模式

• 第一次作业是淳朴的面向过程思想，只有一个Expr类，没有体现出层次化的设计模式，第一次作业，我学会了对象构造方法，把解析的数据传入Expr，再调用Expr中的deriv()进行输出。
• 第二次作业在输入处理上放弃了一个正则表达式到位的思想，改成了分层次处理，先把表达式分割成项，处理项，Wrong Format的处理也分层处理，表达式只管是不是合法的表达式，项只管是不是合法的项，在第三次作业中沿用了这种方法，处理很顺利。为方便求导没有体现出因子的层次，导致第三次重构，合并仍然采用Hashmap<>。
• 第三次作业相比于第二次构建了因子类Fact，我把表达式Expr继承于复合因子Complex，感觉还是有点奇怪的，但他们的数据结构是一样的，不同的是输出方式。输入还是分层处理，求导方面，笔者思维有限，不太理解深浅拷贝的效果，在求导时尽量深拷贝以防意想不到的错误。输出的关键是化简。笔者理应该构建化简类来解耦的，笔者通过递归式的化简-合并完成整个表达式的化简，当然有些地方没化简比如sin(0), cos(0)笔者没有进行幂函数的合并，在笔者的结构中，最好在Term下继承一个类来表示幂函数方便化简。
• 三次作业中没有明确的设计模式，随遇而安，不利于构造清晰的程序结构。

五、心得体会

​ 经过第一单元的学习，我意识到面向对象思想的重要性，因为单纯的面向过程编程可维护性低，难以迭代式开发，导致我重写了2次；其次就是在写程序时必须要注意程序的鲁棒性，对异常输入有识别与处理机制；还有就是不要盲目开写，良好的构思可以效果拔群。