1、学习算法和刷题的框架思维——Go版
前情提示:Go语言学习者。本文参考https://labuladong.gitee.io/algo,代码自己参考抒写,若有不妥之处,感谢指正
关于golang算法文章,为了便于下载和整理,都已开源放在:
- https://github.com/honlu/GoLabuladongAlgorithm
- https://gitee.com/dreamzll/GoLabuladongAlgorithm
方便就请分享,star!备注转载地址!欢迎一起学习和交流!
- 链接参考:
https://labuladong.gitee.io/algo
https://www.runoob.com/go/go-concurrent.html
https://www.kancloud.cn/kancloud/effective/72199
https://books.halfrost.com/leetcode/ChapterFour/0001~0099/0001.Two-Sum/
涉及题目
- leetcode 124 困难
- leetcode 105 难度 Medium
- leetcode 99 难度 Hard,恢复一棵 BST
- Leetcode 46 全排列 中等
首先,这里讲的都是普通的数据结构,咱不是搞算法竞赛的,野路子出生,我只会解决常规的问题。另外,以下是我个人的经验的总结,没有哪本算法书会写这些东西,所以请读者试着理解我的角度,别纠结于细节问题,因为这篇文章就是希望对数据结构和算法建立一个框架性的认识。
从整体到细节,自顶向下,从抽象到具体的框架思维是通用的,不只是学习数据结构和算法,学习其他任何知识都是高效的。
一、数据结构的存储方式
数据结构的存储方式只有两种:数组(顺序存储)和链表(链式存储)。
这句话怎么理解,不是还有散列表、栈、队列、堆、树、图等等各种数据结构吗?
我们分析问题,一定要有递归的思想,自顶向下,从抽象到具体。你上来就列出这么多,那些都属于「上层建筑」,而数组和链表才是「结构基础」。因为那些多样化的数据结构,究其源头,都是在链表或者数组上的特殊操作,API 不同而已。
比如说「队列」、「栈」这两种数据结构既可以使用链表也可以使用数组实现。用数组实现,就要处理扩容缩容的问题;用链表实现,没有这个问题,但需要更多的内存空间存储节点指针。
「图」的两种表示方法,邻接表就是链表,邻接矩阵就是二维数组。邻接矩阵判断连通性迅速,并可以进行矩阵运算解决一些问题,但是如果图比较稀疏的话很耗费空间。邻接表比较节省空间,但是很多操作的效率上肯定比不过邻接矩阵。
「散列表」就是通过散列函数把键映射到一个大数组里。而且对于解决散列冲突的方法,拉链法需要链表特性,操作简单,但需要额外的空间存储指针;线性探查法就需要数组特性,以便连续寻址,不需要指针的存储空间,但操作稍微复杂些。
「树」,用数组实现就是「堆」,因为「堆」是一个完全二叉树,用数组存储不需要节点指针,操作也比较简单;用链表实现就是很常见的那种「树」,因为不一定是完全二叉树,所以不适合用数组存储。为此,在这种链表「树」结构之上,又衍生出各种巧妙的设计,比如二叉搜索树、AVL 树、红黑树、区间树、B 树等等,以应对不同的问题。
了解 Redis 数据库的朋友可能也知道,Redis 提供列表、字符串、集合等等几种常用数据结构,但是对于每种数据结构,底层的存储方式都至少有两种,以便于根据存储数据的实际情况使用合适的存储方式。
综上,数据结构种类很多,甚至你也可以发明自己的数据结构,但是底层存储无非数组或者链表,二者的优缺点如下:
数组由于是紧凑连续存储,可以随机访问,通过索引快速找到对应元素,而且相对节约存储空间。但正因为连续存储,内存空间必须一次性分配够,所以说数组如果要扩容,需要重新分配一块更大的空间,再把数据全部复制过去,时间复杂度 O(N);而且你如果想在数组中间进行插入和删除,每次必须搬移后面的所有数据以保持连续,时间复杂度 O(N)。
链表因为元素不连续,而是靠指针指向下一个元素的位置,所以不存在数组的扩容问题;如果知道某一元素的前驱和后驱,操作指针即可删除该元素或者插入新元素,时间复杂度 O(1)。但是正因为存储空间不连续,你无法根据一个索引算出对应元素的地址,所以不能随机访问;而且由于每个元素必须存储指向前后元素位置的指针,会消耗相对更多的储存空间。
二、数据结构的基本操作
对于任何数据结构,其基本操作无非遍历 + 访问,再具体一点就是:增删查改。
数据结构种类很多,但它们存在的目的都是在不同的应用场景,尽可能高效地增删查改。话说这不就是数据结构的使命么?
如何遍历 + 访问?我们仍然从最高层来看,各种数据结构的遍历 + 访问无非两种形式:线性的和非线性的。
线性就是 for/while 迭代为代表,非线性就是递归为代表。再具体一步,无非以下几种框架:
数组遍历框架,典型的线性迭代结构
func traverse(arr []int){
for i,v := range arr{
// i为下标,v为值。可以迭代访问arr[i]或者直接输出v
}
}
链表遍历框架,兼具迭代和递归结构:
/* 基本的单链表节点 go没有class,只有struct*/
type ListNode struct{
val int
next *ListNode
}
func traverse(head *ListNode){
for ListNode p = head; p != nil; p = p.next{
// 迭代遍历p.val
}
}
func traverse(head *ListNode){
// 前序遍历fmt.println(head.val),正序打印链表
traverse(head.next)
// 后序遍历,倒序打印链表
}
二叉树遍历框架,典型的非线性递归遍历结构:
/*基本的二叉树节点*/
type TreeNode struct{
Val int
Left,Right *TreeNode
}
func traverse(root *TreeNode){
// 前序遍历
traverse(root.Left)
// 中序遍历
traverse(root.Right)
// 后序遍历
}
你看二叉树的递归遍历方式和链表的递归遍历方式,相似不?再看看二叉树结构和单链表结构,相似不?如果再多几条叉,N 叉树你会不会遍历?
二叉树框架可以扩展为 N 叉树的遍历框架:
/* 基本的N叉树节点 */
type TreeNode struct{
val int
children []TreeNode
}
func traverse(root *TreeNode){
for TreeNode child := range root.children{
traverse(child)
}
}
N 叉树的遍历又可以扩展为图的遍历,因为图就是好几 N 叉棵树的结合体。你说图是可能出现环的?这个很好办,用个布尔数组 visited 做标记就行了,这里就不写代码了。
所谓框架,就是套路。不管增删查改,这些代码都是永远无法脱离的结构,你可以把这个结构作为大纲,根据具体问题在框架上添加代码就行了,下面会具体举例。
三、算法刷题指南
首先要明确的是,数据结构是工具,算法是通过合适的工具解决特定问题的方法。也就是说,学习算法之前,最起码得了解那些常用的数据结构,了解它们的特性和缺陷。
那么该如何在 LeetCode 刷题呢?之前的文章写过一些,什么按标签刷,坚持下去云云。现在距那篇文章已经过去将近一年了,我不说那些不痛不痒的话,直接说具体的建议:
先刷二叉树,先刷二叉树,先刷二叉树!
这是我这刷题一年的亲身体会,下图是去年十月份的提交截图:
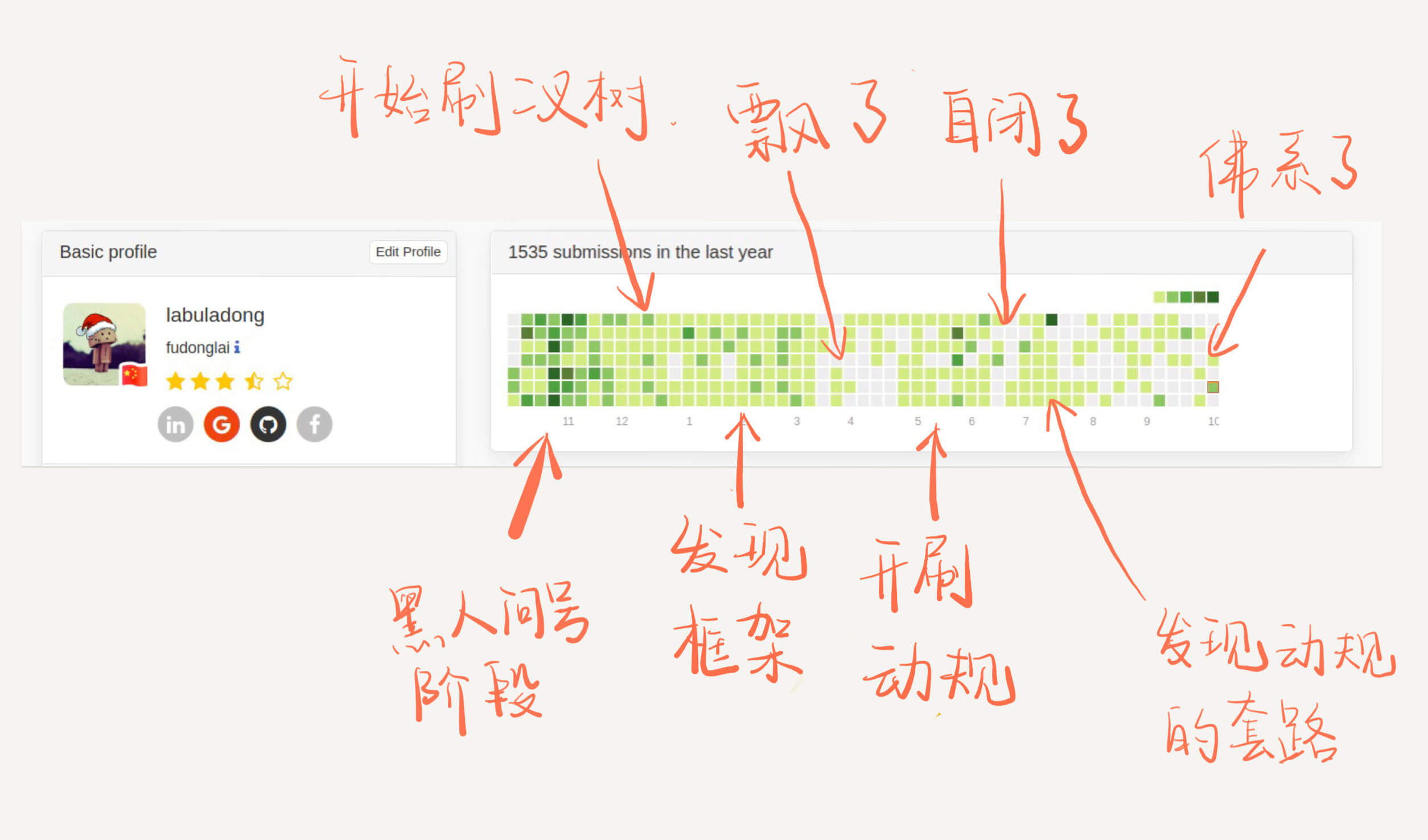
公众号文章的阅读数据显示,大部分人对数据结构相关的算法文章不感兴趣,而是更关心动规回溯分治等等技巧。为什么要先刷二叉树呢,因为二叉树是最容易培养框架思维的,而且大部分算法技巧,本质上都是树的遍历问题。
刷二叉树看到题目没思路?根据很多读者的问题,其实大家不是没思路,只是没有理解我们说的「框架」是什么。
不要小看这几行破代码,几乎所有二叉树的题目都是一套这个框架就出来了:
func traverse(root *TreeNode){
// 前序遍历
traverse(root.Left)
// 中序遍历
traverse(root.Right)
// 后序遍历
}
比如说我随便拿几道题的解法出来,不用管具体的代码逻辑,只要看看框架在其中是如何发挥作用的就行。
LeetCode 124 题,难度 Hard,让你求二叉树中最大路径和,主要代码如下:
func maxPathSum(root *TreeNode) int {
ans := math.MinInt32
var dfs func(root *TreeNode) int
dfs = func(root *TreeNode) int{
if root == nil{
return 0
}
left := max(0, dfs(root.Left))
right := max(0, dfs(root.Right))
// 后序遍历
ans = max(ans, left+right + root.Val)
return max(max(left,right)+root.Val,0)
//
}
dfs(root)
return ans
}
// 因为go不支持重载,因此它只能定义一个min/max函数。于是官方就只实现了最为复杂的浮点型数值的比较,像int这种简单的,就要我们自己实现了
func max(x,y int) int{
if x > y{
return x
}
return y
}
注意:Go:= 只能用于方法内,当定义全局变量时只能通过 var 关键字来定义
注意递归函数的位置,这就是个后序遍历嘛,无非就是把 traverse 函数名字改成 maxPathSum 了。
LeetCode 105 题,难度 Medium,让你根据前序遍历和中序遍历的结果还原一棵二叉树,很经典的问题吧,主要代码如下:
func buildTree(preorder []int, inorder []int) *TreeNode {
if len(preorder)==0 || len(inorder)==0{
return nil
}
// 前序遍历
root := &TreeNode{preorder[0],nil,nil} // root 是指针型
i := 0
for ; i < len(inorder); i++{
if inorder[i] == preorder[0]{
break
}
}
//
root.Left = buildTree(preorder[1:len(inorder[:i])+1], inorder[:i])
root.Right = buildTree(preorder[len(inorder[:i])+1:], inorder[i+1:])
return root
}
不要看这个函数的参数很多,只是为了控制数组索引而已。注意找递归函数的位置,本质上该算法也就是一个前序遍历,因为它在前序遍历的位置加了一坨代码。
LeetCode 99 题,难度 Hard,恢复一棵 BST,主要代码如下【递归、隐式中序遍历,难】:
var x, y, parent *TreeNode
func recoverTree3(root *TreeNode) {
x, y, parent = nil, nil, nil
traverse(root)
x.Val, y.Val = y.Val, x.Val
}
func traverse(root *TreeNode) {
if root == nil {
return
}
traverse(root.Left)
// 中序遍历
if parent != nil && parent.Val > root.Val {
y = root
if x == nil {
x = parent
} else {
return
}
}
parent = root
//
traverse(root.Right)
}
这不就是个中序遍历嘛,对于一棵 BST 中序遍历意味着什么,应该不需要解释了吧。
你看,Hard 难度的题目不过如此,而且还这么有规律可循,只要把框架写出来,然后往相应的位置加东西就行了,这不就是思路吗。
对于一个理解二叉树的人来说,刷一道二叉树的题目花不了多长时间。那么如果你对刷题无从下手或者有畏惧心理,不妨从二叉树下手,前 10 道也许有点难受;结合框架再做 20 道,也许你就有点自己的理解了;刷完整个专题,再去做什么回溯动规分治专题,你就会发现只要涉及递归的问题,都是树的问题。
再举例吧,说几道我们之前文章写过的问题。
在后面的“2 动态规划解题套路框架”中,会说过凑零钱问题,暴力解法就是遍历一棵 N 叉树:
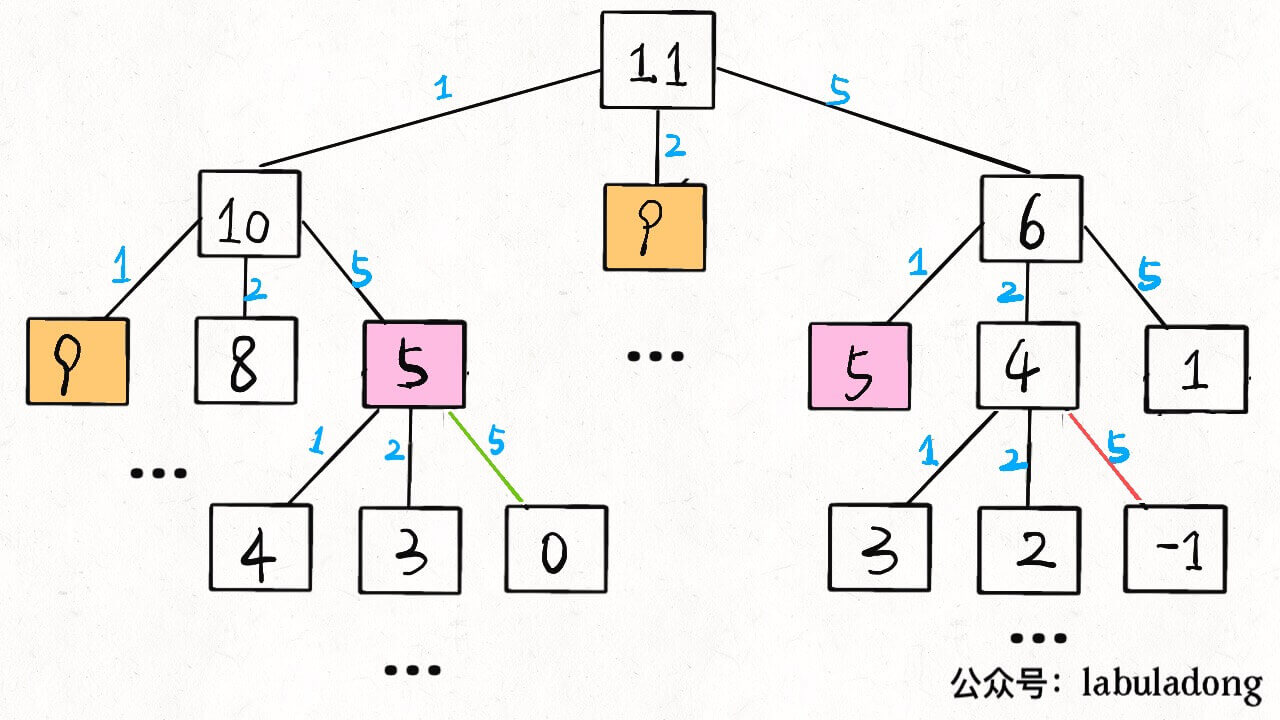
// 以下为伪码
func coinChange(coins []int, amount int){
func dp(n int){
if n==0{return 0}
if n<0{return -1}
res = math.MaxFloat32
for _, coin = range coins{
subproblem = dp(n-coin)
// 子问题无解,跳过
if subproblem == -1{ continue}
res = Min(res, 1+subproblem)
// go 没有三元表达式
if res != math.MaxFloat32{
return res
}else{
return -1
}
}
}
}
func Min(x, y int) int {
if x < y {
return x
}
return y
}
这么多代码看不懂咋办?直接提取出框架,就能看出核心思路了:
// 伪码
func dp(n int){
for _, coin = range roins{
dp(n-coin)
}
}
其实很多动态规划问题就是在遍历一棵树,你如果对树的遍历操作烂熟于心,起码知道怎么把思路转化成代码,也知道如何提取别人解法的核心思路。
再看看回溯算法,前文 "3 回溯算法详解套路框架"直接说了,回溯算法就是个 N 叉树的前后序遍历问题,没有例外。
比如排列组合问题吧,本质上全排列就是在遍历下面这棵树,到叶子节点的路径就是一个全排列:Leetcode 46 全排列 中等
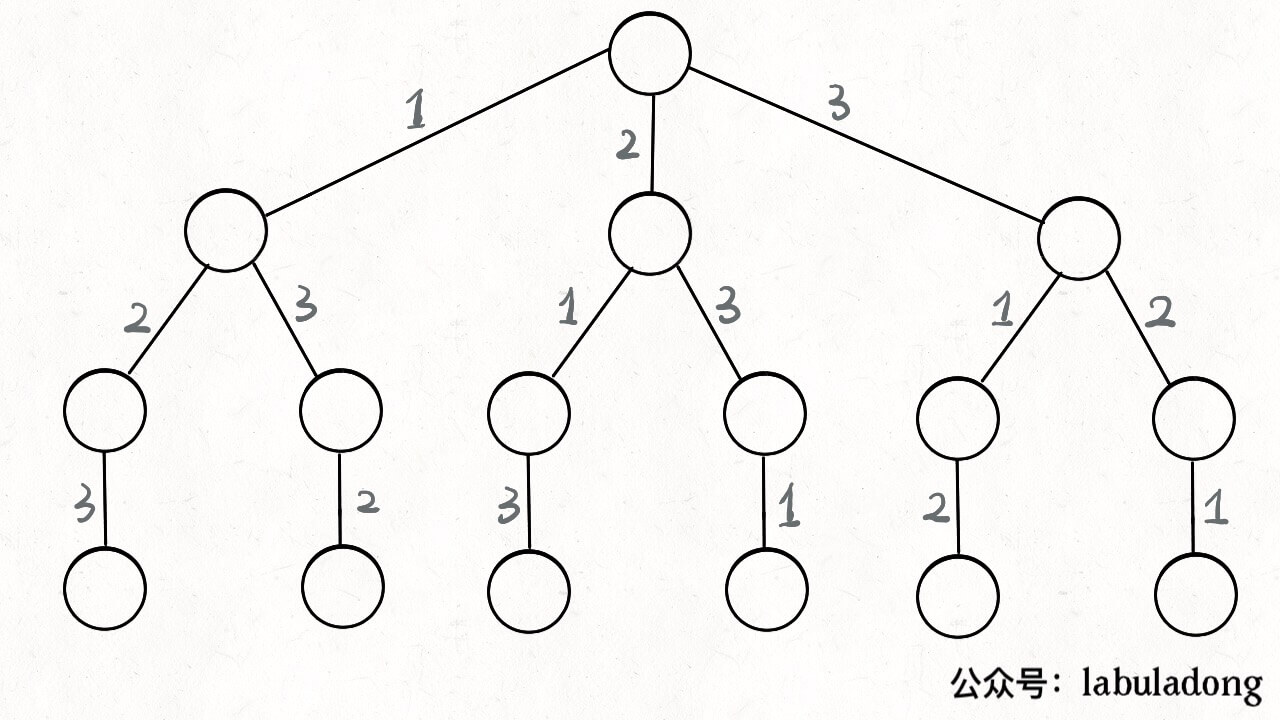
全排列算法的主要代码如下:
//leetcode 46 全排列 回溯算法
var res [][]int
func permute(nums []int) [][]int {
res = [][]int{}
backTrack(nums,len(nums),[]int{})
return res
}
func backTrack(nums []int,numsLen int,path []int) {
if len(nums)==0{
p:=make([]int,len(path))
copy(p,path)
res = append(res,p)
}
for i:=0;i<numsLen;i++{
cur:=nums[i]
path = append(path,cur)
nums = append(nums[:i],nums[i+1:]...)//直接使用切片
backTrack(nums,len(nums),path)
nums = append(nums[:i],append([]int{cur},nums[i:]...)...)//回溯的时候切片也要复原,元素位置不能变
path = path[:len(path)-1]
}
}
// 参考: https://leetcode-cn.com/problems/permutations/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-hui-s-mfrp/
N 叉树的遍历框架,找出来了吧?你说,树这种结构重不重要?
综上,对于畏惧算法的同学来说,可以先刷树的相关题目,试着从框架上看问题,而不要纠结于细节问题。
纠结细节问题,就比如纠结 i 到底应该加到 n 还是加到 n - 1,这个数组的大小到底应该开 n 还是 n + 1?
从框架上看问题,就是像我们这样基于框架进行抽取和扩展,既可以在看别人解法时快速理解核心逻辑,也有助于找到我们自己写解法时的思路方向。
当然,如果细节出错,你得不到正确的答案,但是只要有框架,你再错也错不到哪去,因为你的方向是对的。
但是,你要是心中没有框架,那么你根本无法解题,给了你答案,你也不会发现这就是个树的遍历问题。
这种思维是很重要的, 动态规划详解中总结的找状态转移方程的几步流程,有时候按照流程写出解法,说实话我自己都不知道为啥是对的,反正它就是对了。。。
这就是框架的力量,能够保证你在快睡着的时候,依然能写出正确的程序;就算你啥都不会,都能比别人高一个级别。
四、总结几句
数据结构的基本存储方式就是链式和顺序两种,基本操作就是增删查改,遍历方式无非迭代和递归。
刷算法题建议从「树」分类开始刷,结合框架思维,把这几十道题刷完,对于树结构的理解应该就到位了。这时候去看回溯、动规、分治等算法专题,对思路的理解可能会更加深刻一些。
1、学习算法和刷题的框架思维——Go版的更多相关文章
- 算法笔记刷题1(codeup 1934)
准备6月份的拼题甲级中(本来现在这两天就考试了,但是因为疫情的原因延期了) 刚刚开始按算法笔记刷题,今天是探索codeup的第一天. 一开始并没有把多点测试当回事,直到一错再错,心态爆炸... 附上我 ...
- 算法笔记刷题3(codeup 5901)
今天刷题的速度依旧很慢(小乌龟挥爪.jpg) 我觉得codeup5901中回文串的处理很妙,如果是我自己写的话可能会把数组直接倒过来和原来对比.按照对称规律进行比对的话,工作量可以减少一半. #inc ...
- Python3学习笔记37-LeetCode刷题
LeetCode中国官网一个用来刷编程题的网站,收录了很多面试题.感觉还是学习到很多.记录一下思路.代码还是要多敲. 建议编写完后直接在LeetCode上运行和提交.提交时会有不同的测试用例来测试代码 ...
- 有效的括号序列——算法面试刷题4(for google),考察stack
给定一个字符串所表示的括号序列,包含以下字符: '(', ')', '{', '}', '[' and ']', 判定是否是有效的括号序列. 括号必须依照 "()" 顺序表示, & ...
- 相似的RGB颜色——算法面试刷题3(for google),考察二分
在本题中,每个大写字母代表从“0”到“f”的一些十六进制数字. 红绿蓝三元色#AABBCC可以简写为#ABC. 例如,#15c是颜色#1155cc的简写. 现在,假设两种颜色#ABCDEF和#UVWX ...
- 回文的范围——算法面试刷题2(for google),考察前缀和
如果一个正整数的十进制表示(没有前导零)是一个回文字符串(一个前后读取相同的字符串),那么它就是回文.例如,数字5, 77, 363, 4884, 11111, 12121和349943都是回文. 如 ...
- 有效单词词广场——算法面试刷题5(for google),考察数学
给定一个单词序列,检查它是否构成一个有效单词广场.一个有效的单词广场应满足以下条件:对于满足0≤k<max(numRows numColumns)的k,第k行和第k列对应的字符串应该相同,. 给 ...
- rp算法 随机化 刷题记录
刷随机化是真的会上瘾quq 洛谷P3973 [TJOI2015]线性代数 看oiwiki上说可以随机化...于是... 就随机在a[i]上选一位取反,然后更新答案,最后输出答案. ...无话可说 代码 ...
- 算法笔记刷题5(PAT A1025)
第一次上手PAT的甲级题目,瑟瑟发抖(英语不好对着题目愣了半天) 这一题的要点是使用sort函数. 使用sort函数必须使用 #include <algorithm> using name ...
随机推荐
- [atARC062F]Painting Graphs with AtCoDeer
求出点双后缩点,对于点双之间,显然不存在简单环,即每一个简单环一定在一个点双内部,换言之即每一个点双可以独立的考虑,然后将结果相乘 (对于点双之间的边任意染色,即若有$s$条边,还会有$k^{s}$的 ...
- 从零开始学Kotlin第七课
1.强制类型转换需要在后面加两个感叹号 2.如果需要在java代码调用kotlin的方法时候使用文件名+kt.方法 3.object 类名 是创建匿名内部类的写法 调用 传入class对象 4.在to ...
- Insights直播回顾,对话专家,HMS Core 6创新能力解读
HMS Core Insights第八期直播–对话专家,HMS Core 6创新能力解读,已于11月25日圆满结束,本期直播与小伙伴们一同了解了HMS Core 6在图形.媒体以及连接与通信领域推出的 ...
- JavaWeb 请求转发重定向
请求转发和重定向 request除了可以作为请求对象之外,还可以作为域对象,但是该域对象的取值范围,是一次请求范围之内(浏览器地址栏没有发生跳转访问别的资源) 作用:将servlet中的数据通过req ...
- Atcoder Regular Contest 123 题解
u1s1 我是真的不知道为什么现场这么多人切了 D,感觉 D 对思维要求显然要高于其他 300+ 人切掉的 D 吧(也有可能是 Atc 用户整体水平提升了?) A 开 幕 雷 击(这题似乎 wjz 交 ...
- Git 使用,本地项目上传到GitHub远程库
Git 使用,本地项目上传到GitHub远程库 环境 GitHub账号 点此进入github官网 git客户端工具 点此进入git下载页 本地项目上传到 GitHub 在GitHub中创建一个仓库(远 ...
- 【宏组学】如何根据taxid(或taxname)快速获得taxname(或taxid)?
需求 我有一个物种taxonomy ID的list,想获得相应的物种名,不要一个个去NCBI Taxonomy官网查.反之根据物种名list查询对应的taxid. 实现 因为之前没怎么用过,我的第一个 ...
- [linux] 非root安装Python2及其模块
需求 系统自带的python2版本太低,且没有想要的模块,非root用户无法安装.有些模块是python2写的,无法用python3,所以自己下载一个高版本的python2,可以自由下载模块. 实现 ...
- python故障
问题: ImportError: No module named dns.resolver 解决: 通过包管理工具pip安装dnspython pip install dnspython
- linux 常用查看命令
linux 常用查看命令 目录 linux 常用查看命令 linux 查看内存/进程-ps/top linux 查看磁盘存储-df linux 查看io读写-iotop linux 查看端口占用-ne ...
