深入理解索引和AVL树、B-树、B+树的关系

目录

• 什么是索引
• 索引的分类
• 索引和AVL树、B-树、B+树的关系
• AVL树、红黑树
• B-树
• B+树
• SQL和NoSQL索引

什么是索引

索引时数据库的一种数据结构，数据库与索引的关系可以看作书籍和目录的关系。当用户通过索引查找数据时，好比用户通过目录查询某章节的某个知识点。这样可以帮助用户提高查找速度。所以，索引可以提高数据库的性能。

索引的分类

从物理存储角度:

聚簇索引和非聚簇索引

从数据结构角度:

B-树、B+树、hash索引、FULLTEXT索引、R-Tree索引

从逻辑角度:

• 主键索引：主键索引是一种特殊的唯一索引，不允许有空值
• 普通索引/单列索引
• 复合索引/多列索引：复合索引指多个字段上创建的索引，只有在查询条件中使用了创建索引时的第一个字段，索引才会被使用。使用复合索引时遵循最左前缀集合
• 唯一索引或者非唯一索引
• 空间索引：空间索引是对空间数据类型的字段建立的索引，MYSQL中的空间数据类型有4种，分别是GEOMETRY、POINT、LINESTRING、POLYGON

索引和AVL树、B-树、B+树的关系

传统用来搜索的平衡二叉树有很多，如 AVL 树，红黑树等。这些树在一般情况下查询性能非常好，但当数据非常大的时候它们就无能为力了。原因当数据量非常大时，内存不够用，大部分数据只能存放在磁盘上，只有需要的数据才加载到内存中。一般而言，磁盘和内存的数据交互是影响系统性能的瓶颈，所以索引的效率依赖于磁盘 IO 的次数。

AVL树、红黑树

即平衡二叉搜索树，它的特点是在二叉搜索树（BST）的基础上，要求每个节点的左子树和右子树的高度差至多为1。这个要求使AVL的高度h = logn，底数为2，避免了BST可能存在的单链极端情况（h = n）。

它通过旋转来保持平衡的，而旋转是对整棵树的操作，若部分加载到内存中则无法完成旋转操作，所以AVL树的操作要全部加载加到内存中。

红黑树则是BST得另一个变种，增加了颜色限制，它也需要通过旋转调整结构，所以AVL树和红黑树基本都是存储在内存中才会使用的数据结构。在大规模数据数据存储的时候，显然不能将全部数据全部加载进内存，因此如果采用红黑树和AVL树，就会造成频繁IO。所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了。

索引的原理其实是不断的缩小查找范围，就如我们平时用字典查单词一样，先找首字母缩小范围，再第二个字母等等。平衡二叉树是每次将范围分割为两个区间。为了更快，我们可以每次将范围分割为多个区间，区间越多，定位数据越快越精确，这就是B、B+树这类树的由来。

B-树

也叫B树，即平衡多路查找树，m阶B树表示节点可拥有的最多m个孩子，2-3树是3阶B树，2-3-4树是4阶B树。多叉树可以有效降低树的高度，h=log_m(n)，m为log的底数。

B-树的特点：

1. 任意非叶子结点最多只有 M 个儿 子， M>2
2. 根结点的儿子数为 [2, M]
3. 除根结点以外的非叶子结点的儿子数为 [M/2, M]
4. 每个结点存放至少 M/2-1 （向上取整）和至多 M-1 个关键字, M> 2
5. 非叶子结点的关键字个数 = 指向孩子的指针个数 -1 ；
6. 非叶子结点的关键字： K[1], K[2], …, K[M-1] ， K[i] < K[i+1]
7. 非叶子结点的指针： P[1], P[2], …, P[M] ；其中 P[1] 指向关键字小于 K[1] 的子树， P[M] 指向关键字大于 K[M-1] 的子树，其它 P[i] 指向关键字属于 (K[i-1], K[i]) 的子树
8. 所有叶子结点位于同一层

B-树结构如下图：

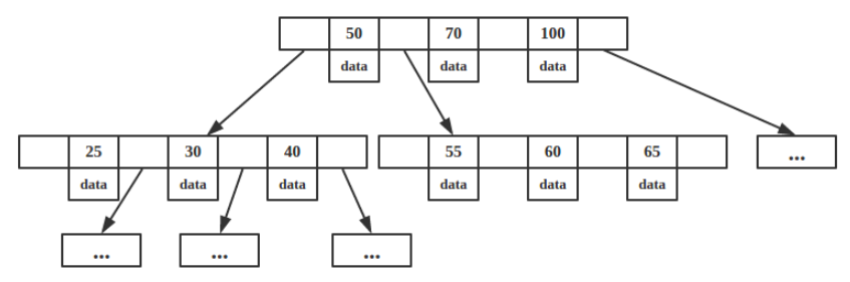
在普通平衡二叉树中，插入删除后若不满足平衡条件则进行旋转 操作，而在B树中，插入删除后不满足条件则进行分裂及合并操作。所以，B树并不需要把节点一次性加载到内存，而B树的查找过程是一个顺指针查找节点和节点中查找关键字的交叉过程。

B树查找虽然很方便，但是存在一个缺陷，如果我们要完成对数据的遍历，那么需要不断在内外存做数据交互，这显然是影响性能的。为了解决这个问题，提出了B+树。

B+树

B-树的变体，也是一种多路搜索树，与B-树的区别是：

1. 非叶子结点的子树指针与关键字个数相同，即n 个 key 值的节点指针域为 n 而不是 n+1
2. 非叶子结点的子树指针 P[i] ， 指向关键字值属于 [K[i], K[i+1]) 的子树（ 左闭右开，B树是全开区间）
3. 为所有叶子结点增加一个链指针
4. B+树的key 的副本存储在内部节点，真正的 key 和 data 存储在叶子节点上 。

B+树结构如下图：

B+树的两个明显特点：

• 数据只出现在叶子节点
• 所有叶子节点增加了一个链指针

总结一下B树和B+树的不同：

1. 因为内节点并不存储 data，所以一般B+树的叶节点和内节点大小不同，而B-树的每个节点大小一般是相同的。在磁盘存储中，为了满足局部性原理，一般会给每个结点分配一页的存储容量，这使得B+树的非叶节点可以保存更多的key，减少了查找时的磁盘IO次数。
2. B+ 树只有达到叶子结点才命中（ B树可以在非叶子结点命中），其查询时间复杂度固定为 log n，查询效率很稳定，而B-树查询时间复杂度不固定，与 key 在树中的位置有关。
3. B+树叶节点两两相连可大大增加区间访问性，可使用在范围查询，而B树每个节点 key 和 data 在一起，无法区间查找。

SQL和NoSQL索引

MongoDB采用B树作为索引，MySQL采用B+树作为聚簇索引的数据结构。

这是因为关系型数据库和非关系型数据的设计方式上的不同，导致在关系型数据中，遍历操作比较常见，因此采用B+树作为索引比较合适。而在非关系型数据库中，单一查询比较常见，因此采用B树作为索引，比较合适。

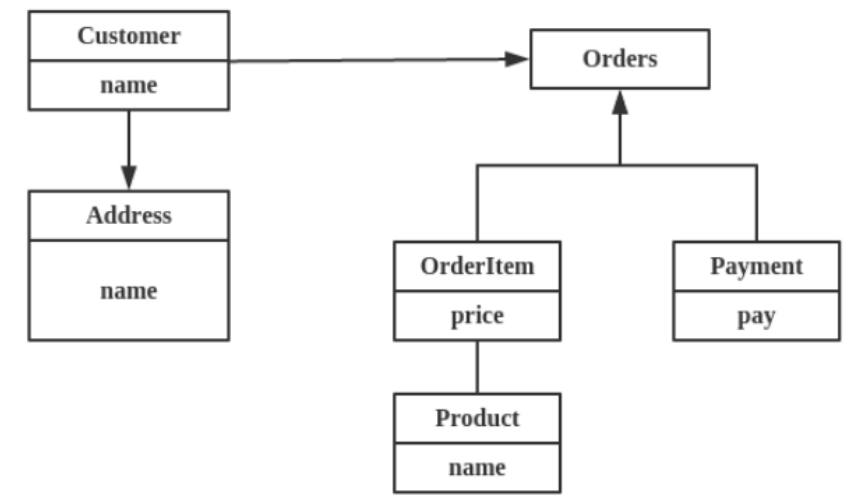
MongoDB 是文档型的数据库，是一种 nosql，它使用类 Json 格式保存数据。文档型数据库和我们常见的关系型数据库不同，一般使用 XML 或 Json 格式来保存数据，归属于聚合型数据库，键值型的redis也属于聚合型。对于聚合型数据库，key-value聚合在一起的b树可以减少磁盘 IO。

聚合型数据库的结构：

参考

谈谈你对mysql索引的认识

MongoDB及Mysql背后的B/B+树

为什么 MongoDB （索引）使用B-树而 Mysql 使用 B+树