sigma网格中水平压力梯度误差及其修正

1.水平梯度误差产生

sigma坐标系下，笛卡尔坐标内水平梯度项对应形式为

\[\begin{equation}
\left. \frac{\partial }{\partial x} \right|_z = \left. \frac{\partial }{\partial x} \right|_{\sigma} + \frac{\partial }{\partial \sigma} \frac{\partial \sigma}{\partial x}
\end{equation}\]

当采用数值格式对等式右端进行离散时，产生的截断误差远远大于等式左端。一些情况下，水平压力梯度（horizontal pressure gradient）误差无法随 \(\sigma\) 分层加密而减小，即静压不连续（hydrostatic inconsistency）情形。下面通过两个算例演示水平梯度误差产生原因，并介绍目前已有的主要修正方法。

1.1.示例1

在 Beckmann（1992）文章中，采用如下 \(\sigma\) 变换方程

\[\begin{equation}
\sigma = 2 \frac{z}{h} + 1
\end{equation}\]

对应的水平梯度算子为

\[\begin{equation}
\left. \nabla \right|_z = \left. \nabla \right|_{\sigma} + (1 - \sigma)\frac{\nabla h}{h} \frac{\partial }{\partial \sigma}
\end{equation}\]

在此 \(\sigma\) 坐标下，原始压力梯度（OPG）为

\[\begin{equation}
OPG = h \left[\frac{\partial \phi}{\partial x} + (1 - \sigma)\frac{\partial }{\partial \sigma}\left(\frac{\phi}{h}\right) \frac{\partial h}{\partial x} \right]
\end{equation}\]

采用有限差分格式对其离散得

\[\begin{equation}
OPG(FD) = \frac{\bar{h}}{\Delta x}\times \left[(\phi_i - \phi_{i-1}) + (1 - \sigma)\frac{1}{2}\frac{\partial }{\partial \sigma}\left(\frac{\phi_i}{h_i} + \frac{\phi_{i-1}}{h_{i-1}} \right)\Delta h \right]
\end{equation}\]

这里 \(\bar{h} = \frac{1}{2}(h_i + h_{i-1})\)，\(\Delta h = (h_i - h_{i-1})\)，i 为节点水平编号。

假设标量 \(\phi\) 只沿垂向变化，其分布函数为

\[\begin{equation}
\phi(x) = \sum_{k = 1}^{K} \phi_k \left( \frac{2z}{H_0} \right)^k
\end{equation}\]

由于 \(\phi\) 与 x 无关，因此其水平梯度为0。将上式代入水平梯度差分形式表达式 （ OPG(FD) ）中，得

\[\begin{equation}
ERROR(OPG) = \sum_{k = 1}^{K} \phi_k (\sigma - 1)^k \frac{\bar{h}}{H_0^k \Delta x}\times \left[ (h_i^k - h_{i-1}^k) - \frac{k}{2}\Delta h (h_i^{k-1} - h_{i-1}^{k-1}) \right]
\end{equation}\]

通过上述误差公式可知，当标量 \(\phi(z)\) 只包含 \(k = 0,1,2\) 三项时误差为0。对于更高阶多项式 \(\phi(z)\) 则具有误差表达式

\[\begin{equation}
ERROR(OPG) = \sum_{k = 1}^{K} \phi_k (\sigma - 1)^k \frac{\bar{h}}{H_0^k \Delta x} R_1
\end{equation}\]

其中

\[\begin{equation}
R_1 = {(1 + r)^k - (1-r)^k - rk[(1+r)^{k-1} + (1-r)^{k-1}]} \quad \text{with} \quad r = \frac{\Delta h}{2\bar{h}} = \frac{h_i - h_{i-1}}{h_i + h_{i-1}}
\end{equation}\]

1.2.示例2

Haney (1991) 与 Mellor (1993) 先后给出了静压连续条件表达形式

\[\begin{equation}
\left| \frac{\sigma}{H} \frac{\delta_x H}{\delta \sigma} \right| < 1
\end{equation}\]

其中 \(\sigma = \frac{z}{H} \in [-1, 0]\)。在此 \(\sigma\) 网格内，水平梯度表达形式为

\[\begin{equation}
\left. \frac{\partial \phi}{\partial x} \right|_z = \left. \frac{\partial \phi}{\partial x} \right|_{\sigma} - \frac{\sigma}{H} \frac{\partial H}{\partial x} \frac{\partial \phi}{\partial \sigma}
\end{equation}\]

与 Beckmann 采用方法相同，Mellor 也采用差分格式（FDM）对 \(\sigma\) 坐标内水平梯度进行离散。与其不同的是，Mellor 将标量 \(\phi(z)\) 在节点 \(z_0 = \bar{\sigma} \bar{H}\) 处进行泰勒展开

\[\begin{equation}
\phi(z) = \phi_0 + \left( \frac{\partial b}{\partial z} \right)_0 [\sigma H(x) - z_0] + \left( \frac{\partial^2 b}{\partial z^2} \right)_0 \frac{[\sigma H(x) - z_0]^2}{2} + \cdots
\end{equation}\]

并将展开式代入水平梯度离散方程中

\[\begin{equation}
\left. \frac{\delta b}{\delta x} \right|_z = \frac{b_{i,k} + b_{i,k-1} - b_{i-1,k} - b_{i-1,k-1}}{2\delta x} - \frac{\bar{\sigma} \delta_x H}{\bar{H} \delta x} \frac{b_{i,k-1} + b_{i-1,k-1} - b_{i,k} - b_{i-1,k}}{2 \delta \sigma}
\end{equation}\]

得

\[\begin{equation}
E\left( \left. \frac{\delta b}{\delta x} \right|_z \right) = \frac{H}{4} \frac{\delta_x H}{\delta x} \left[ \left( \frac{\partial^2 b }{\partial z^2} \right) + \frac{\sigma H}{3}\left(\frac{\partial^3 b}{\partial z^3} \right) + \cdots \right] \times \left( (\delta \sigma)^2 - \sigma^2 \left( \frac{\delta_x H}{H} \right)^2 \right)
\end{equation}\]

其中，\(\delta_x H = H_i - H_{i-1}\)，\(\delta \sigma = \sigma_{k-1} - \sigma_k\)。

由 Mellor 给出的误差公式可以看出，当 \(\left| (\sigma \delta_x H)/(H \delta \sigma) \right| = 1\) 时，右端离散项误差为0。但是当 \(\left| (\sigma \delta_x H)/(H \delta \sigma) \right| > 1\) 时，对于给定的 \(\left| \delta_x H/H \right|\)，当 \(\delta \sigma/\sigma\) 减小时（垂向加密），误差反而增大，即所谓的“静压不连续”（hydrostatic inconsistent）现象。

1.3.使用z坐标的 FEM 或 DGM 亦不能幸免

可以看出，在 \(\sigma\) 网格中水平压力误差产生的主要原因，是梯度项对应的离散格式截断误差不能相消使其无法收敛导致，所以只要不采用 \(\sigma\) 坐标或避免梯度分裂为两项就可避免此种误差。遗憾的是，即使采用 z 坐标的 FEM 或 DGM 格式也不能避免此种误差。采用一个简单的示例来说明，海洋模型中常用的三棱柱单元，如下图所示

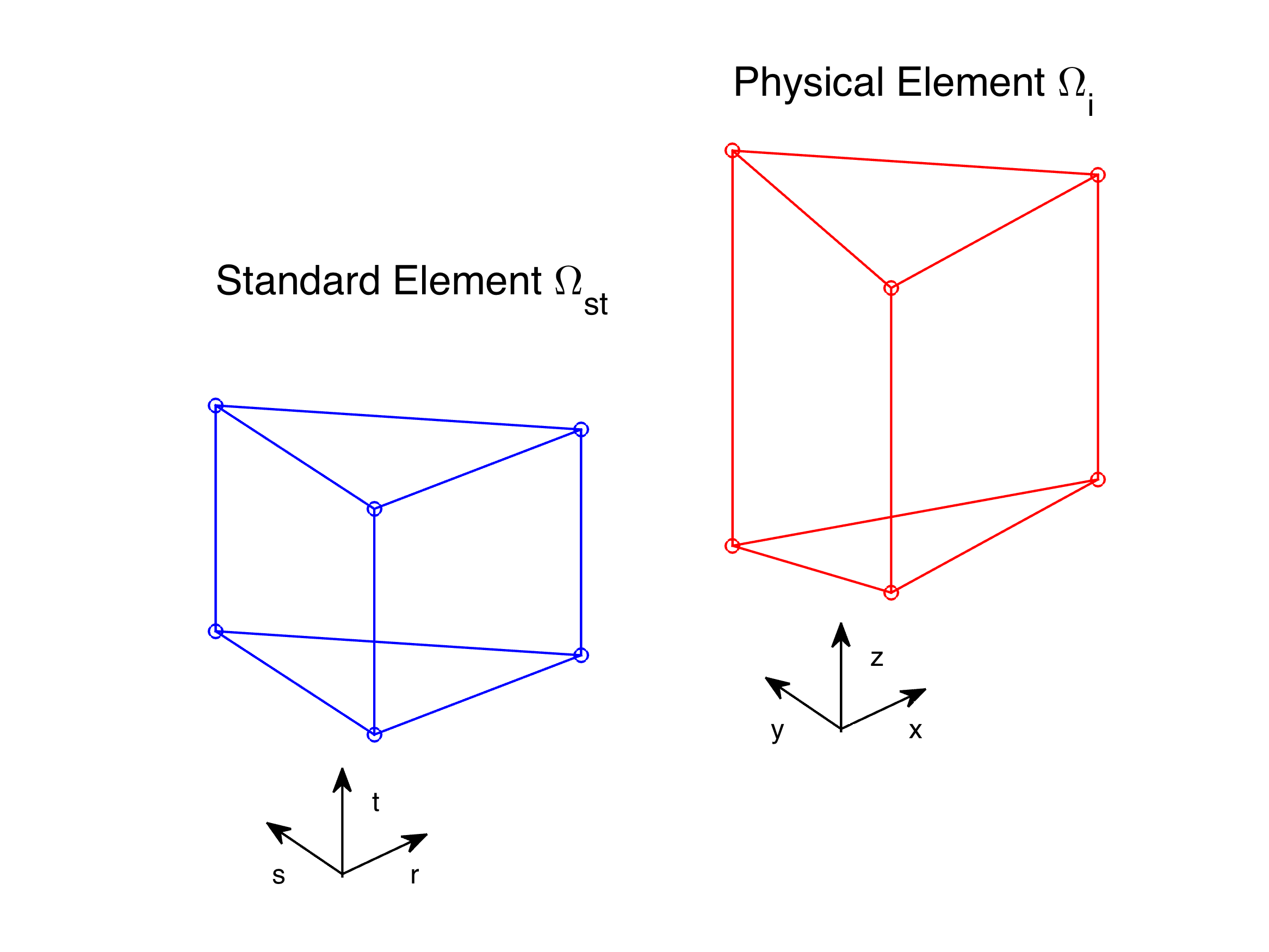
在实际计算过程中，物理单元通过 Jacobian 变换到标准单元，所有算子（微分，积分）在标准单元上进行计算，随后将计算结果通过逆变换获得物理单元计算结果。其中映射关系如下

\[\begin{equation}
x = x(r,s,t) \quad
y = y(r,s,t) \quad
z = z(r,s,t)
\end{equation}\]

在计算三棱柱内水平梯度时，根据链式法则

\[\begin{equation}
\left. \frac{\partial }{\partial x} \right|_{\Omega_i} = \frac{\partial r}{\partial x} \left. \frac{\partial }{\partial r} \right|_{\Omega_{st}} + \frac{\partial s}{\partial x} \left. \frac{\partial }{\partial s} \right|_{\Omega_{st}} + \frac{\partial t}{\partial x} \left. \frac{\partial }{\partial t} \right|_{\Omega_{st}}
\end{equation}\]

可以看出，在FEM或DGM方法中，水平梯度的求解同样会引入与 \(\sigma\) 网格变换类似的误差。

2.修正方法

为了减小水平压力梯度误差，众学者提出多种方法，Shchepetkin (2003) 主要将其分为以下两种。

2.1.Pressure Jacobian

在垂向坐标中使用交错网格形式，其中压力 \(P_{k+1/2}\) 位于密度节点中间，对于相邻两层水体，计算时将 \(P_{k+1/2}\) 插值到一个合适的计算层上，随后得到压力梯度。这种方法在大气科学中广泛采用，主要不同形式是插值方式，一般以线性插值或二次插值为主，也有三次插值。

2.2.Density Jacobian

此方法由 Blumberg 和 Mellor (1987) 与 Song (1998) 等提出。此种方法特点是将积分与微分互换位置。首先根据静压假定有

\[\begin{equation}
\frac{\partial }{\partial z} \left( \frac{\partial P}{\partial x} \right) = - g \frac{\partial \rho}{\partial x}
\end{equation}\]

将上式在垂向上进行积分，并将表层压力梯度表达式代入，得

\[\begin{equation}
-\left. \frac{\partial P}{\partial x} \right|_z = -\left. \frac{\partial P}{\partial x} \right|_{z = \xi} - g \int_z^{\xi} \left. \frac{\partial \rho}{\partial x} \right|_z d\sigma = -g\rho(\xi) \frac{\partial \xi}{\partial x} - \int_z^{\xi} \left. \frac{\partial \rho}{\partial x} \right|_z d\sigma
\end{equation}\]

这种方法通过将微分与积分交换位置，使得仅采用线性插值与积分也可以较为准确的计算压力梯度，可有效减小误差。

2.3.Other vertical grids

上述方法都是讨论如何尽量较小误差，并没有将误差完全消除。更为直接的方法就是避免采用如 \(\sigma\) 网格形式，而直接采用 z 坐标方法。在底部地形变化较大地区，将 z 坐标与 Shaved Cell 方法结合，也可以获得较为准确的考虑底部地形变化的模拟结果。

附录A.

1.图片代码（Matlab）

clear all; close all

r = [-1, 1, -1, -1, 1, -1];
s = [-1, -1, 1, -1, -1, 1];
t = [-1, -1, -1, 1, 1, 1];

LToV = [1,2; 2,3; 3,1; 4,5; 5,6; 6,4; 1,4; 2,5; 3,6];

figure('Color', 'w');

plot3(r(LToV'), s(LToV'), t(LToV'), 'ob-'); hold on;

t_h = text(r(3), s(3), mean(t)+ 2 ,'Standard Element \Omega_{st}');
set(t_h, 'FontSize', 18)

x = [-1, 1, -1, -1, 1, -1]+5;
y = [-1, -1, 1, -1, -1, 1];
z = [-1.5, -1.2, -2, 1.2, 1.5, 1.5];

plot3(x(LToV'), y(LToV'), z(LToV'), 'or-');
t_h = text(x(3), y(3), mean(t)+ 2 ,'Physical Element \Omega_{i}');
set(t_h, 'FontSize', 18)

axis equal;

grid on;
axis off