《BI那点儿事》三国人物智力分布状态分析
献给广大的三国爱好者们,希望喜欢三国的朋友一起讨论,加深对传奇三国时代的了解
数据分析基础概念:
数据分为“不可测量”的数据和“可测量”的数据。
不可测量的数据称为“分类数据”(Category Data或Categorical Data。),而可测量的数据称为“数值数据”(Numerical Data)。
组中值:Class Midpoint
次数:Frequency
相对次数:Relative Frequency
相对次数=所属各组的数据个数÷数据总数
次数分布表和直方图
组距分组掩盖了各组内间的数据分布状况,为反映各组数据的一般水平,我们通常用组中值来作为该组数据的一个代表值(class midpoint)。上限与下限之间的中点数值称为组中值,它是各组上下限数值的简单平均,即组中值=(下限+上限)/2。
若遇到开口组,则上开口组组中值=下限+邻组组距/2; 下开口组组中值=上限-邻组组距/2。
使用组中值代表一组数据时有一个必要的假定条件,即各组数据在本组内呈现均匀分布或在组中值两侧呈对称分布。如果实际数据的分布不符合这一假定,用组中值作为一组数据的代表就会有一定的误差。
建立数据分析环境:
SELECT CASE WHEN 智力 > 0
AND 智力 < 10 THEN '0-9'
WHEN 智力 >= 10
AND 智力 < 20 THEN '10-19'
WHEN 智力 >= 20
AND 智力 < 30 THEN '20-29'
WHEN 智力 >= 30
AND 智力 < 40 THEN '30-39'
WHEN 智力 >= 40
AND 智力 < 50 THEN '40-49'
WHEN 智力 >= 50
AND 智力 < 60 THEN '50-59'
WHEN 智力 >= 60
AND 智力 < 70 THEN '60-69'
WHEN 智力 >= 70
AND 智力 < 80 THEN '70-79'
WHEN 智力 >= 80
AND 智力 < 90 THEN '80-89'
WHEN 智力 >= 90
AND 智力 <= 100 THEN '90-100'
END 分组 ,
COUNT(*) 人数
FROM FactSanguo11
GROUP BY CASE WHEN 智力 > 0
AND 智力 < 10 THEN '0-9'
WHEN 智力 >= 10
AND 智力 < 20 THEN '10-19'
WHEN 智力 >= 20
AND 智力 < 30 THEN '20-29'
WHEN 智力 >= 30
AND 智力 < 40 THEN '30-39'
WHEN 智力 >= 40
AND 智力 < 50 THEN '40-49'
WHEN 智力 >= 50
AND 智力 < 60 THEN '50-59'
WHEN 智力 >= 60
AND 智力 < 70 THEN '60-69'
WHEN 智力 >= 70
AND 智力 < 80 THEN '70-79'
WHEN 智力 >= 80
AND 智力 < 90 THEN '80-89'
WHEN 智力 >= 90
AND 智力 <= 100 THEN '90-100'
END
ORDER BY 分组 SELECT *
FROM FactSanguo11
WHERE 智力 >= 90
AND 智力 <= 100
ORDER BY 智力 DESC
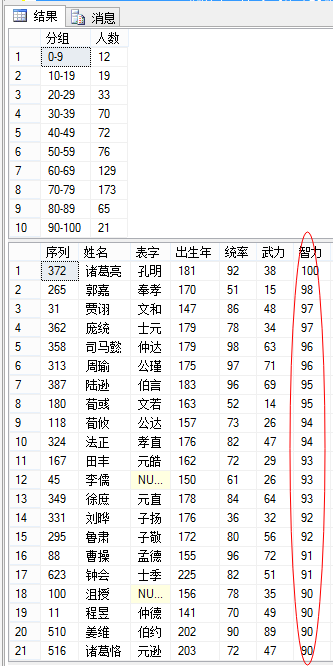
三国人物智力分布表
|
智力分组 |
组中值 |
人数 |
相对次数 |
|
0-9 |
5 |
12 |
0.02 |
|
10-19 |
14.5 |
19 |
0.03 |
|
20-29 |
25 |
33 |
0.05 |
|
30-39 |
34.5 |
70 |
0.10 |
|
40-49 |
44.5 |
72 |
0.11 |
|
50-59 |
54.5 |
76 |
0.11 |
|
60-69 |
64.5 |
129 |
0.19 |
|
70-79 |
74.5 |
173 |
0.26 |
|
80-89 |
84.5 |
65 |
0.10 |
|
90-100 |
95 |
21 |
0.03 |
|
合计 |
670 |
1.00 |
直方图: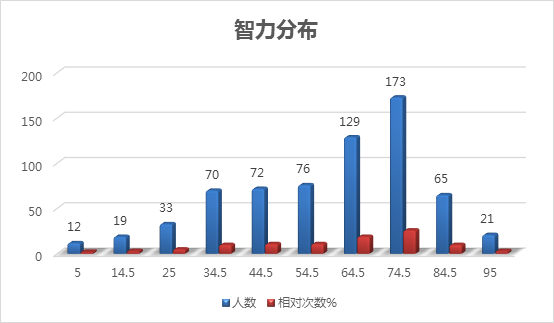
如各位所见,上表中的组距是9。之所以选择9,并没有什么数学上的规定,而是全由本人主观决定的。没错,组距该设多少,完全依照分析者本身的判断。
以主观设定的组距而做成的人数分布表没有说服力,无法在他人面前公开,难道就没有按数学原理制定组距的方法吗?也许有人会产生这样的疑问。事实上,方法是有的。

以步骤2求出的组距为基础,做出如下的人数分布表:
|
智力分组 |
组中值 |
人数 |
相对次数 |
|
0-10 |
5 |
13 |
0.02 |
|
11-20 |
15 |
18 |
0.03 |
|
21-30 |
25 |
39 |
0.06 |
|
31-40 |
35 |
71 |
0.11 |
|
41-50 |
45 |
70 |
0.10 |
|
51-60 |
55 |
78 |
0.12 |
|
61-70 |
65 |
146 |
0.22 |
|
71-80 |
75 |
160 |
0.24 |
|
81-90 |
85 |
58 |
0.09 |
|
91-100 |
95 |
17 |
0.03 |
|
合计 |
670 |
1.02 |
直方图:
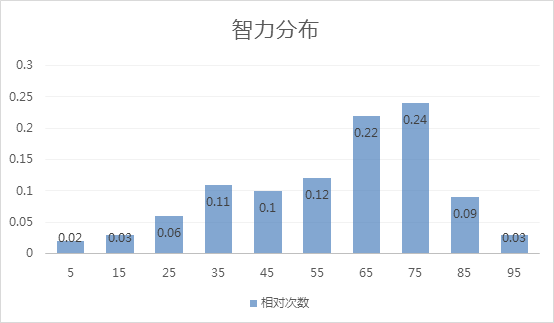
《BI那点儿事》三国人物智力分布状态分析的更多相关文章
- 《BI那点儿事—数据的艺术》目录索引
原创·<BI那点儿事—数据的艺术>教程免费发布 各位园友,大家好,我是Bobby,在学习BI和开发的项目的过程中有一些感悟和想法,整理和编写了一些学习资料,本来只是内部学习使用,但为了方便 ...
- 《BI那点儿事》Microsoft 聚类分析算法——三国人物身份划分
什么是聚类分析? 聚类分析属于探索性的数据分析方法.通常,我们利用聚类分析将看似无序的对象进行分组.归类,以达到更好地理解研究对象的目的.聚类结果要求组内对象相似性较高,组间对象相似性较低.在三国数据 ...
- 《BI那点儿事》Microsoft 决策树算法——找出三国武将特性分布,献给广大的三国爱好者们
根据游戏<三国志11>武将数据,利用决策树分析,找出三国武将特性分布.其中变量包括统率.武力.智力.政治.魅力.身分.变量说明:统率:武将带兵出征时的部队防御力.统帅越高受到普通攻击与兵法 ...
- 《BI那点儿事》双变量的相关分析——相关系数
例如,“三国人物是否智力越高,政治就越高”,或是“是否武力越高,统率也越高:准备数据分析环境: SELECT * FROM FactSanguo11 WHERE 姓名 IN ( N'荀彧', N'荀攸 ...
- Characters_of_the_Three_Kingdoms - 三国人物结构化数据
Characters_of_the_Three_Kingdoms - 三国人物结构化数据 三国人物结构化数据 为什么会有这个项目 需求1:摆脱网上那些长篇累牍的文章: 需求2:只是想简单查看下人物姓甚 ...
- 《BI那点儿事》运用标准计分和离差——分析三国超一流统帅综合实力排名 绝对客观,数据说话
数据分析基础概念:标准计分: 1.无论作为变量的满分为几分,其标准计分的平均数势必为0,而其标准差势必为1.2.无论作为变量的单位是什么,其标准计分的平均数势必为0,而其标准差势必为1.公式为: 离差 ...
- 《BI那点儿事》SSRS图表和仪表——雷达图分析三国超一流谋士、统帅数据(图文并茂)
雷达图分析三国超一流谋士.统帅数据,献给广大的三国爱好者们,希望喜欢三国的朋友一起讨论,加深对传奇三国时代的了解 建立数据环境: -- 抽取三国超一流谋士TOP 10数据 DECLARE @t1 TA ...
- 《BI那点儿事》三国数据分析系列——蜀汉五虎上将与魏五子良将武力分析,绝对的经典分析
献给广大的三国爱好者们,希望喜欢三国的朋友一起讨论,加深对传奇三国时代的了解 数据分析基础概念:集中趋势分析是指在大量测评数据分布中,测评数据向某点集中的情况.总体(population)是指客观存在 ...
- Microsoft Naive Bayes 算法——三国人物身份划分
Microsoft朴素贝叶斯是SSAS中最简单的算法,通常用作理解数据基本分组的起点.这类处理的一般特征就是分类.这个算法之所以称为“朴素”,是因为所有属性的重要性是一样的,没有谁比谁更高.贝叶斯之名 ...
随机推荐
- windows下安装 sphinx 数据库全文搜索引擎
此次演示的环境是:win7系统,64位,php5.4.x,apache sphinx,斯芬克斯(英语不好的同学可以直接读这个音),意狮身人面像 特点:创建索引速度快,3分钟左右能创建100万条记录的索 ...
- 基于XMPP协议(openfire服务器)的消息推送实现
转自:http://blog.csdn.net/nomousewch/article/details/8088277 最近好像有不少朋友关注Android客户端消息推送的实现,我在之前的项目中用到过J ...
- 【Android测试】【第十二节】Uiautomator——API详解
◆版权声明:本文出自carter_dream的博客,转载必须注明出处. 转载请注明出处:http://www.cnblogs.com/by-dream/p/4921701.html 简单的例子 以一个 ...
- 带AI的俄罗斯方块源码
好久没写俄罗斯方块的游戏了.从学习编程到现在,相继用Win32 API.MFC.C.C#.JS.iOS写过大约二十款左右的俄罗斯方块游戏.最近用Cocos2d-x写了一下,第一次完全将游戏逻辑与UI层 ...
- 访问 Android Developers 403 错误
原因: 以前改过 hosts. 现在用的 威-屁-恩. 解决办法: 把改过的 hosts 删掉就行了.
- Cross-site Scripting (XSS) 阅读笔记
本文源自 https://www.owasp.org/index.php/Cross-site_Scripting_%28XSS%29 通过阅读和翻译,并按照自己的理解,整理成如下文档. 概述 XSS ...
- Ubuntu下编译运行C#——mono tools
编译C#代码用mono-csc,直接编译成二进制可执行文件: mono-csc a.cs b.cs c.cs d.cs 如果一个工程里文件很多,可以使用通配符“*”: mono-csc *.cs
- 获取手机通讯录--ios
- (void)test { //这个变量用于记录授权是否成功,即用户是否允许我们访问通讯录 int __block tip=0; //声明一个通讯簿的引用 ABAdd ...
- C# 窗体
窗体的事件:删除事件:先将事件页面里面的挂好的事件删除,再删后台代码里面的事件 Panel是一个容器 1.Label -- 文本显示工具Text:显示的文字取值.赋值:lable1.Text 2.Te ...
- 使用NetBeans搭建基于Spring框架的Web应用
NetBeans下载链接:https://netbeans.org/. 第一步:选择“文件”菜单下的“新建项目”: 第二步:类别选择“Java Web”,项目选择“Web应用程序”,单击“下一步”: ...
