插头DP讲解+[BZOJ1814]:Ural 1519 Formula 1(插头DP)
1.什么是插头$DP$?
插头$DP$是$CDQ$大佬在$2008$年的论文中提出的,是基于状压$D$P的一种更高级的$DP$多用于处理联通问题(路径问题,简单回路问题,多回路问题,广义回路问题,生成树问题)。
插头$DP$每道题都不一样,且需要进行较为繁琐的分类讨论,所以插头$DP$十分锻炼思维的严谨性和全面性。
2.插头$DP$思路
$\mathcal{A.}$状态确立
$\alpha.$插头
插头表示一种联通状态。
在棋盘模型中,一个格子有向某方向的插头,表示这个格子在这个方向与插头那边的格子相连。
注意:插头并不是说将要去某处的虚拟状态,而是已经到达某处的现实状态。
我们需要考虑的是接下来往哪里走,因为如果有一个插头指向当前格子,说明当前格子已经与插头的来源有联通了。
有了插头,就方便多啦,我们一般需要的是进行逐格递推,通俗的讲,就是跑一遍。
$\beta.$轮廓线
轮廓线就是一条分界线,至于它为什么叫轮廓线,我也不知道,就像$CDQ$为什么叫$CDQ$一样,她也不知道,但是她爸妈知道。
你可以感性的将它理解为是“已经决策了的格子”与“还没有决策的格子”的分界线。
但是,轮廓线的用途不止如此。
轮廓线还兼容了存储这条分界线上插头状态的作用。
需要注意的是,假设一行内有$m$个格子,那么会有$m+1$个插头,为什么呢?
看一下下面的这张图:
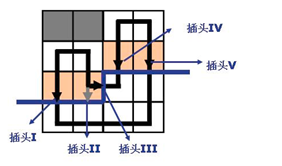
显然一行内有$4$个格子,但是有$5$个插头,多出来的那一个插头在当前正在决策的那个格子的右侧。
个人习惯将插头编号为$1~m$。
一般数据范围比较小,我们可以用状压来存储,即定义$dp[i][j][state]$表示当前决策到$(i,j)$这个点,状态为$state$的方案数(或代价,$etc$)。
$\gamma.$插头与轮廓线的结合
插头与轮廓线结合在一起,就会碰撞出一些美丽的火花。
我们递归的时候就是依据插头的存在性,来求出所有能转移到的合法状态。
在回路问题中,对于一个状态一个格子恰好有两个插头,一个“进来”,一个“出去”。
$\mathcal{B}.$记录状态
下面来介绍三种记录状态的方式:
$\alpha.$最小表示法
为了方便,所有有障碍的格子记为$0$,第一个非障碍的格子以及所有与它相连的格子标记为$1$,第一个未标记的格子以及与它相邻的格子标记为$2$……
重复以上的过程,直到所有的格子都标记完毕。
举个栗子:
$1,2,5$联通,$3,6$联通,$4$自己和自己卡在一起,那么其最小表示法即为${1,1,2,3,1,2}$。
$\beta.$括号表示法
先来看一个性质:假设一条轮廓线上有$4$个插头$a,b,c,d$,$a$与$c$联通且不与$b$联通,那么$b$与$d$肯定也不联通。
这个性质很重要,因为它适用于所有的棋盘问题。
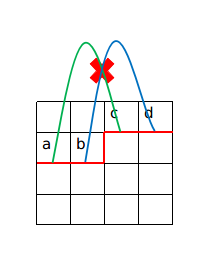
就像这样,显然如果$b$与$d$也相交的话就不可能满足情况了。
再具体一点:
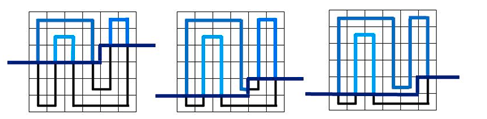
相信细心的你一定会发现,轮廓先上方的路径都是由若干条互不相交的路径构成的,原因就是再上面那张图。
每条路径上的两个端点也会恰好对应轮廓线上的两个插头。
再来明确一点,对于不同的插头,我们称它们为左插头或右插头,并不是指它们的方向,而是指在途中相对的左右,如下图:
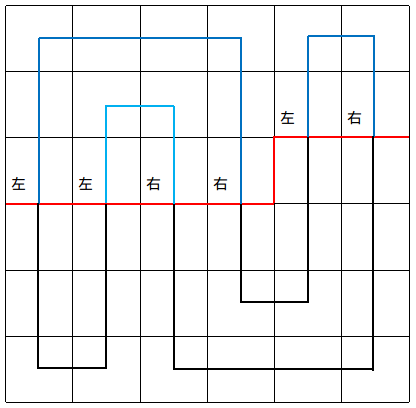
有点跑题了,这种“不交叉”很容易让我们联想到括号匹配,左括号为进栈,右括号为出栈,左括号一定与右括号一一对应。
当然有可能会让你想到卡特兰数,这点很重要,能帮你卡常。
$\gamma.$状态的编码
利用状压的思想,我们将每行$m+1$个状态用一个$m+1$位的$k$进制数表示,在做题的时候建议将$k$改为$2$的$n$次幂,方便进行为运算,运行速度会有很大的提升(前提空间允许)。
小技巧:如需大范围修改联通状态,可以选择$\Theta(m)$将其解码到一个数组里,修改后在$\Theta(n)$将其计算为$k$进制数,而对于只需要进行局部修改的情况可以直接用$(x\ div\ p^{i-1})mod\ p$来获取第i位的状态,使用$+x\times p^{i-1}$来对第i位的状态进行修改。
$\mathcal{C}.$状态转移
$\alpha.$行间转移
显然,第$i$行第$j$列的下插头决定了第$i+1$行第$j$列有没有上插头,因此需要将这个信息传递给下一行。
当枚举到一行的最后一个格子的时候,第$m$个插头一定为$0$(即为没有),如下图。

细心的你还能发现,在行间转移之前的第$0~m-1$个插头会变成行间转移之后的第$1~m$个插头,如下图。
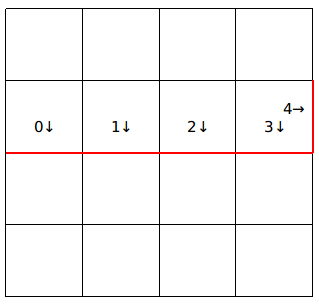
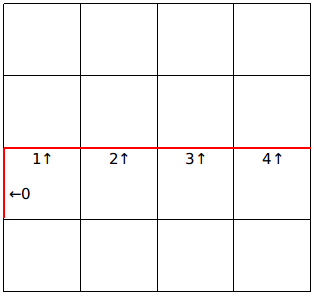
所以,我们每次只需要将上一行的状态左移一位即可。
代码$\downarrow$:
for(int j=1;j<=cnts[cnt];j++)state[cnt][j]<<=1;
打法奇特,请多谅解。
$\beta.$逐格转移
因题而异,比行间转移复杂,一般分为多种情况,需要分类讨论。
在很多的状态转移中都出现了以下三种情况:
$\mathfrak{a}.$新建一个联通分量:
这个情况只出现在转移位置的轮廓线上没有下插头和右插头:
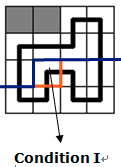
在上图中,这个格子没有上插头,也没有左插头,那么由于我们要遍历整张图,所以我们要新建插头,把这个格子与其他格子连起来,相应的,我们要把原来轮廓线对应位置的插头改为$1$。
$\mathfrak{b}.$合并两个联通分量:
不连通的话,当然这样做会把他们变联通:
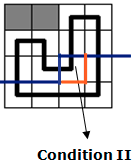
这个位置有上插头,也有左插头。由于我们不要求只有一条回路,因此回路可以在这里结束。我们直接更新答案即可。
$\mathfrak{c}.$保持原有的联通分量:
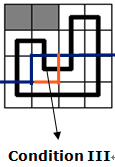
只有一个插头。那么这个插头可以向其他方向走:向下和向右均可以。所以我们修改一下轮廓线并更新对应状态的答案即可。
$\mathcal{D}.$优化
可以使用$hash$表进行优化,下面附一个此题中我用的$hash$表的代码$\downarrow$:
int pre_hash[600000],at;
int sta_hash[2][600000],cnts[2];
void hash_map(int sta,long long val)
{
int key=sta%590027;
for(int i=pre_hash[key];i;i=hash[i].nxt)
if(sta_hash[cnt][hash[i].to]==sta)//如果这个状态已经存在,就加上
{dp[cnt][hash[i].to]+=val;return;}
sta_hash[cnt][++cnts[cnt]]=sta;//不存在这个状态就新建
dp[cnt][cnts[cnt]]=val;
hash[++at].nxt=pre_hash[key];
hash[at].to=cnts[cnt];
pre_hash[key]=at;
}
例题$\downarrow$
题目描述
一个$m\times n$的棋盘,有的格子存在障碍,求经过所有非障碍格子的哈密顿回路个数。
输入格式
第$1$行,$n,m$。
从第$2$行到第$n+1$行,每行一段字符串($m$个字符),"*"表不能铺线,"."表必须铺。
输出格式
输出一个整数,表示总方案数。
样例
样例输入$1$:
4 4
**..
....
....
....
样例输出$1$:
样例输入$2$:
4 4
....
....
....
....
样例输出$2$:
数据范围与提示
$2\leqslant n,m\leqslant 12$。
题解
典型的插头$DP$板子题,洛谷更是将它作为了【模板】插头$dp$。
这道题中,我们需要用$3$进制来表示状态,$0$表示无插头,$1$表示左插头,$2$表示右插头,我使用的是$4$进制,弃掉一位,但是方便位运算的操作。
下面来列举一下这道题的$7$种情况:
$\alpha.$有障碍:
if(!Map[i][j]){if(!down&&!right)hash_map(sta,ans);}
$\beta.$ :
:
if(!down&&!right){if(Map[i+1][j]&&Map[i][j+1])hash_map(sta+2*(1<<bit[j])+(1<<bit[j-1]),ans);}
$\gamma.$ :
:
if(down&&!rght)
{
if(Map[i][j+1])hash_map(sta,ans);
if(Map[i+1][j])hash_map(sta+down*((1<<bit[j-1])-(1<<bit[j])),ans);
}
$\delta.$ :
:
if(!down&&right)
{
if(Map[i+1][j])hash_map(sta,ans);
if(Map[i][j+1])hash_map(sta+right*((1<<bit[j])-(1<<bit[j-1])),ans);
}
$\epsilon.$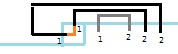 :
:
if(down==1&&rght==1)
{
int count=1;
for(int l=j+1;l<=m;l++)
{
if((sta>>bit[l])%4==1)count++;
if((sta>>bit[l])%4==2)count--;
if(!count)
{
hash_map(sta-(1<<bit[j])-(1<<bit[j-1])-(1<<bit[l]),ans);
break;
}
}
}
注意此时我们不仅需要将两个左插头减去,而且还要将左边的右插头变成左插头。
$\zeta.$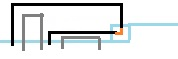 :
:
if(down==2&&rght==2)
{
int count=1;
for(int l=j-2;l>=0;l--)
{
if((sta>>bit[l])%4==1)count--;
if((sta>>bit[l])%4==2)count++;
if(!count)
{
hash_map(sta-2*(1<<bit[j])-2*(1<<bit[j-1])+(1<<bit[l]),ans);
break;
}
}
}
注意上面依然需要减去两个右插头,再把右边的左插头变成右插头。
$\eta.$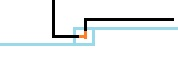 :
:
if(down==1&&rght==2){hash_map(sta-(1<<bit[j])-2*(1<<bit[j-1]),ans);}
此时我们合并了一个右插头和一个左插头,减去就好了。
$\theta.$形成了一个回路,只有在最后一个格子才有可能形成回路。
if(down==2&&rght==1&&i==endx&&j==endy)ansss+=ans;
$7$种情况已经列举完了,代码实现细节不少,要注意。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct hash_table
{
int nxt;
int to;
}hash[600000];
char ch[20];
int pre_hash[600000],at;
int sta_hash[2][600000],cnts[2];
bool Map[15][15];
int bit[15];
bool cnt;
int endx,endy;
long long ans,ansss,dp[2][600000];
void hash_map(int sta,long long val)//hash表
{
int key=sta%590027;
for(int i=pre_hash[key];i;i=hash[i].nxt)
if(sta_hash[cnt][hash[i].to]==sta)
{dp[cnt][hash[i].to]+=val;return;}
sta_hash[cnt][++cnts[cnt]]=sta;
dp[cnt][cnts[cnt]]=val;
hash[++at].nxt=pre_hash[key];
hash[at].to=cnts[cnt];
pre_hash[key]=at;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",ch+1);
for(int j=1;j<=m;j++)
if(ch[j]=='.')
{
Map[i][j]=1;
endx=i;
endy=j;
}
}
for(int i=1;i<=m;i++)//预处理一下,方便下面处理
bit[i]=(i<<1);
cnts[0]=1;
dp[0][1]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=cnts[cnt];j++)sta_hash[cnt][j]<<=2;//将状态左移一位
for(int j=1;j<=m;j++)
{
at=0;
memset(pre_hash,0,sizeof(pre_hash));
cnt^=1;
cnts[cnt]=0;
for(int k=1;k<=cnts[cnt^1];k++)
{
int sta=sta_hash[cnt^1][k];//提取状态
long long ans=dp[cnt^1][k];
int down=(sta>>bit[j])%4;//提取插头信息,下同
int rght=(sta>>bit[j-1])%4;
if(!Map[i][j])//α
{if(!down&&!rght)hash_map(sta,ans);}
else if(!down&&!rght)//β
{if(Map[i+1][j]&&Map[i][j+1])hash_map(sta+2*(1<<bit[j])+(1<<bit[j-1]),ans);}
else if(down&&!rght)//γ
{
if(Map[i][j+1])hash_map(sta,ans);
if(Map[i+1][j])hash_map(sta+down*((1<<bit[j-1])-(1<<bit[j])),ans);
}
else if(!down&&rght)//δ
{
if(Map[i+1][j])hash_map(sta,ans);
if(Map[i][j+1])hash_map(sta+rght*((1<<bit[j])-(1<<bit[j-1])),ans);
}
else if(down==1&&rght==1)//ε
{
int count=1;
for(int l=j+1;l<=m;l++)
{
if((sta>>bit[l])%4==1)count++;
if((sta>>bit[l])%4==2)count--;
if(!count)
{
hash_map(sta-(1<<bit[j])-(1<<bit[j-1])-(1<<bit[l]),ans);
break;
}
}
}
else if(down==2&&rght==2)//ζ
{
int count=1;
for(int l=j-2;l>=0;l--)
{
if((sta>>bit[l])%4==1)count--;
if((sta>>bit[l])%4==2)count++;
if(!count)
{
hash_map(sta-2*(1<<bit[j])-2*(1<<bit[j-1])+(1<<bit[l]),ans);
break;
}
}
}
else if(down==1&&rght==2)//η
{hash_map(sta-(1<<bit[j])-2*(1<<bit[j-1]),ans);}
else if(down==2&&rght==1&&i==endx&&j==endy)ansss+=ans;//θ
}
}
}
printf("%lld",ansss);
return 0;
}
rp++
插头DP讲解+[BZOJ1814]:Ural 1519 Formula 1(插头DP)的更多相关文章
- bzoj1814 Ural 1519 Formula 1(插头dp模板题)
1814: Ural 1519 Formula 1 Time Limit: 1 Sec Memory Limit: 64 MBSubmit: 924 Solved: 351[Submit][Sta ...
- BZOJ1814: Ural 1519 Formula 1(插头Dp)
Description Regardless of the fact, that Vologda could not get rights to hold the Winter Olympic gam ...
- 【BZOJ1814】Ural 1519 Formula 1 插头DP
[BZOJ1814]Ural 1519 Formula 1 题意:一个 m * n 的棋盘,有的格子存在障碍,求经过所有非障碍格子的哈密顿回路个数.(n,m<=12) 题解:插头DP板子题,刷板 ...
- bzoj 1814 Ural 1519 Formula 1 插头DP
1814: Ural 1519 Formula 1 Time Limit: 1 Sec Memory Limit: 64 MBSubmit: 942 Solved: 356[Submit][Sta ...
- bzoj1814 Ural 1519 Formula 1(插头DP)
对插头DP的理解还不是很透彻. 先说一下肤浅的理解吧. 插头DP使用范围:指数级复杂度,且适用于解决网格图连通性问题,如哈密顿回路等问题.插头一般指每相邻2个网格的接口. 题目难度:一般不可做. 使用 ...
- bzoj1814: Ural 1519 Formula 1 动态规划 插头dp
http://acm.timus.ru/problem.aspx?space=1&num=1519 题目描述 一个 m * n 的棋盘,有的格子存在障碍,求经过所有非障碍格子的哈密顿回路个数. ...
- bzoj 1814 Ural 1519 Formula 1 ——插头DP
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=1814 普通的插头 DP .但是调了很久.注意如果合并两个 1 的话,不是 “把向右第一个 2 ...
- Ural 1519 Formula 1 插头DP
这是一道经典的插头DP单回路模板题. 用最小表示法来记录连通性,由于二进制的速度,考虑使用8进制. 1.当同时存在左.上插头的时候,需要判断两插头所在连通块是否相同,若相同,只能在最后一个非障碍点相连 ...
- bzoj 1814: Ural 1519 Formula 1 插头dp经典题
用的括号序列,听说比较快. 然并不会预处理,只会每回暴力找匹配的括号. #include<iostream> #include<cstdio> #include<cstr ...
随机推荐
- yum安装php7
1.安装epel源 yum -y install epel-release yum -y install http://dl.fedoraproject.org/pub/epel/epel-relea ...
- QML - 实现Gstreamer投屏 投屏画面遮挡
1. 背景介绍 中控端运行的操作系统是Android,中控软件主要功能有导航.收音机.媒体(音乐).蓝牙(连接).手机互联.行车辅助和系统设置等. 仪表端运行的操作系统是Linux,仪表软件主 ...
- RHEL 无图形界面安装oracle 11gr2
RHEL7.3 无图形界面安装oracle 11gr2 使用纯命令安装方式.提供RHEL全量系统镜像. 1.oracle官方下载地址:https://www.oracle.com/techne ...
- PHP数据结构基本概念
原文:https://www.cnblogs.com/crystaltu/p/6408484.html 学习任何一种技术都应该先清楚它的基本概念,这是学习任何知识的起点!本文是讲述数据结构的基本概念, ...
- docker下部署kafka集群(多个broker+多个zookeeper)
网上关于kafka集群的搭建,基本是单个broker和单个zookeeper,测试研究的意义不大.于是折腾了下,终于把正宗的Kafka集群搭建出来了,在折腾中遇到了很多坑,后续有时间再专门整理份搭建问 ...
- Redis主从架构核心原理
Redis-Cluster工作原理: redis集群内置了16384个哈希槽,当需要在 Redis 集群中放置一个 key-value 时,redis 先对 key 使用 crc16 算法算出一个结果 ...
- Jpa/Hibernate ManyToOne 关联非主键列 延迟加载失效
@ManyToOne配置延迟加载,如果是关联主键列, @ManyToOne(fetch = FetchType.LAZY) @JoinColumn(name = "billid", ...
- luogu P5338 [TJOI2019]甲苯先生的滚榜
传送门 首先,排名系统,一看就知道是原题,可以上平衡树来维护 然后考虑一种比较朴素的想法,因为我们要知道排名在一个人前面的人数,也就是AC数比他多的人数+AC数一样并且罚时少的人数,所以考虑维护那两个 ...
- HTML-图片和多媒体
1.图片和多媒体 (1) 图片:img元素 src 属性:图片路径: alt 属性:图片无法显示时使用的替代文字: title:鼠标悬停时显示的文字 : <img src="图片 ...
- IDEA tomcat热部署方法
项目开发过程中,我们一般希望在修改完代码之后不重启项目即可提现出修改的结果,那么热部署项目就显得十分必要了.在idea中将项目热部署至tomcat中的方法如下: 首先打开tomcat配置界面,在ser ...
