kmeans与kmeans++的python实现

一.kmeans聚类：

基本方法流程

1.首先随机初始化k个中心点

2.将每个实例分配到与其最近的中心点，开成k个类

3.更新中心点，计算每个类的平均中心点

4.直到中心点不再变化或变化不大或达到迭代次数

优缺点：该方法简单，执行速度较快。但其对于离群点处理不是很好，这是可以去除离群点。kmeans聚类的主要缺点是随机的k个初始中心点的选择不够严谨，因为是随机，所以会导致聚类结果准确度不稳定。

二.kmeans++聚类：

kmeans++方法是针对kmeans的主要缺点进行改进，通过在初始中心点的选择上改进不足。

中心点的选择：

1.首先随机选择一个中心点

2.计算每个点到与其最近的中心点的距离为dist，以正比于dist的概率，随机选择一个点作为中心点加入中心点集中，重复直到选定k个中心点

对于正比于dist的概率随机选择一个数据点作为新的中心点的理解有一个英文资料解释如下：

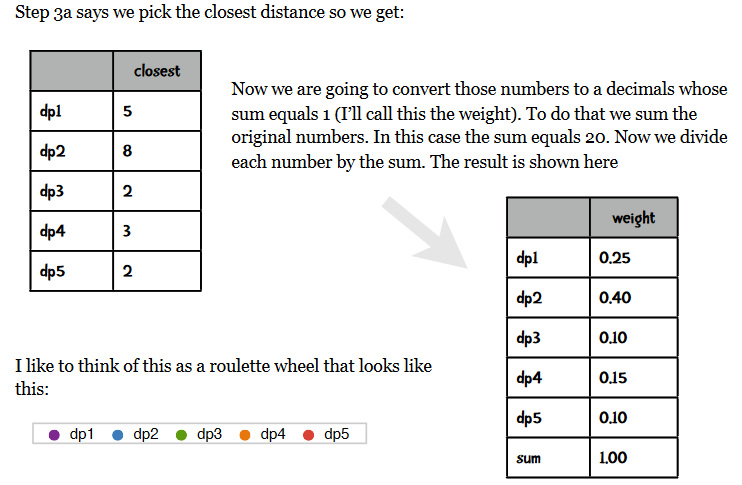
3.计算同kmeans方法

三.评估方法

误差平方和可以评估每次初始中心点选择聚类的优劣，公式如下：

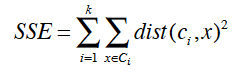
计算每个点到它自己的类的中心点的距离的平方和，外层是不同类间的和。根据每次初始点的选择聚类结果计算SSE，SSE值越小结果越好。

四.代码

 #!/usr/bin/python
 # -*- coding: utf-8 -*-
 import math
 import codecs
 import random

 #k-means和k-means++聚类，第一列是label标签，其它列是数值型数据
 class KMeans:

     #一列的中位数
     def getColMedian(self,colList):
         tmp = list(colList)
         tmp.sort()
         alen = len(tmp)
         if alen % 2 == 1:
             return tmp[alen // 2]
         else:
             return (tmp[alen // 2] + tmp[(alen // 2) - 1]) / 2

     #对数值型数据进行归一化，使用绝对标准分[绝对标准差->asd=sum(x-u)/len(x),x的标准分->(x-u)/绝对标准差，u是中位数]
     def colNormalize(self,colList):
         median = self.getColMedian(colList)
         asd = sum([abs(x - median) for x in colList]) / len(colList)
         result = [(x - median) / asd for x in colList]
         return result

     '''
     1.读数据
     2.按列读取
     3.归一化数值型数据
     4.随机选择k个初始化中心点
     5.对数据离中心点距离进行分配
     '''
     def __init__(self,filePath,k):
         self.data={}#原始数据
         self.k=k#聚类个数
         self.iterationNumber=0#迭代次数
         #用于跟踪在一次迭代改变的点
         self.pointsChanged=0
         #误差平方和
         self.SSE=0
         line_1=True
         with codecs.open(filePath,'r','utf-8') as f:
             for line in f:
                 # 第一行为描述信息
                 if line_1:
                     line_1=False
                     header=line.split(',')
                     self.cols=len(header)
                     self.data=[[] for i in range(self.cols)]
                 else:
                     instances=line.split(',')
                     column_0=True
                     for ins in range(self.cols):
                         if column_0:
                             self.data[ins].append(instances[ins])# 0列数据
                             column_0=False
                         else:
                             self.data[ins].append(float(instances[ins]))# 数值列
         self.dataSize=len(self.data[1])#多少实例
         self.memberOf=[-1 for x in range(self.dataSize)]

         #归一化数值列
         for i in range(1,self.cols):
             self.data[i]=self.colNormalize(self.data[i])

         #随机从数据中选择k个初始化中心点
         random.seed()
         #1.下面是kmeans随机选择k个中心点
         #self.centroids=[[self.data[i][r] for i in range(1,self.cols)]
         #                for r in random.sample(range(self.dataSize),self.k)]
         #2.下面是kmeans++选择K个中心点
         self.selectInitialCenter()

         self.assignPointsToCluster()

     #离中心点距离分配点，返回这个点属于某个类别的类型
     def assignPointToCluster(self,i):
         min=10000
         clusterNum=-1
         for centroid in range(self.k):
             dist=self.distance(i,centroid)
             if dist<min:
                 min=dist
                 clusterNum=centroid
         #跟踪改变的点
         if clusterNum!=self.memberOf[i]:
             self.pointsChanged+=1
         #误差平方和
         self.SSE+=min**2
         return clusterNum

     #将每个点分配到一个中心点，memberOf=[0,1,0,0,...]，0和1是两个类别，每个实例属于的类别
     def assignPointsToCluster(self):
         self.pointsChanged=0
         self.SSE=0
         self.memberOf=[self.assignPointToCluster(i) for i in range(self.dataSize)]

     # 欧氏距离,d(x,y)=math.sqrt(sum((x-y)*(x-y)))
     def distance(self,i,j):
         sumSquares=0
         for k in range(1,self.cols):
             sumSquares+=(self.data[k][i]-self.centroids[j][k-1])**2
         return math.sqrt(sumSquares)

     #利用类中的数据点更新中心点，利用每个类中的所有点的均值
     def updateCenter(self):
         members=[self.memberOf.count(i) for i in range(len(self.centroids))]#得到每个类别中的实例个数
         self.centroids=[
             [sum([self.data[k][i] for i in range(self.dataSize)
                   if self.memberOf[i]==centroid])/members[centroid]
              for k in range(1,self.cols)]
             for centroid in range(len(self.centroids))]

     '''迭代更新中心点（使用每个类中的点的平均坐标），
     然后重新分配所有点到新的中心点，直到类中成员改变的点小于1%(只有不到1%的点从一个类移到另一类中)
     '''
     def cluster(self):
         done=False
         while not done:
             self.iterationNumber+=1#迭代次数
             self.updateCenter()
             self.assignPointsToCluster()
             #少于1%的改变点，结束
             if float(self.pointsChanged)/len(self.memberOf)<0.01:
                 done=True
         print("误差平方和（SSE）: %f" % self.SSE)

     #打印结果
     def printResults(self):
         for centroid in range(len(self.centroids)):
             print('\n\nCategory %i\n=========' % centroid)
             for name in [self.data[0][i] for i in range(self.dataSize)
                 if self.memberOf[i]==centroid]:
                 print(name)

     #kmeans++方法与kmeans方法的区别就是初始化中心点的不同
     def selectInitialCenter(self):
         centroids=[]
         total=0
         #首先随机选一个中心点
         firstCenter=random.choice(range(self.dataSize))
         centroids.append(firstCenter)
         #选择其它中心点，对于每个点找出离它最近的那个中心点的距离
         for i in range(0,self.k-1):
             weights=[self.distancePointToClosestCenter(x,centroids)
                      for x in range(self.dataSize)]
             total=sum(weights)
             #归一化0到1之间
             weights=[x/total for x in weights]

             num=random.random()
             total=0
             x=-1
             while total<num:
                 x+=1
                 total+=weights[x]
             centroids.append(x)
         self.centroids=[[self.data[i][r] for i in range(1,self.cols)] for r in centroids]

     def distancePointToClosestCenter(self,x,center):
         result=self.eDistance(x,center[0])
         for centroid in center[1:]:
             distance=self.eDistance(x,centroid)
             if distance<result:
                 result=distance
         return result

     #计算点i到中心点j的距离
     def eDistance(self,i,j):
         sumSquares=0
         for k in range(1,self.cols):
             sumSquares+=(self.data[k][i]-self.data[k][j])**2
         return  math.sqrt(sumSquares)

 if __name__=='__main__':
     kmeans=KMeans('filePath',3)
     kmeans.cluster()
     kmeans.printResults()

参考：1.machine.learning.an.algorithmic.perspective.2nd.edition.

　　　 2.a programmer's guide to data mining