[Python3 练习] 005 汉诺塔1 递归解法

题目：汉诺塔 I

(1) 描述

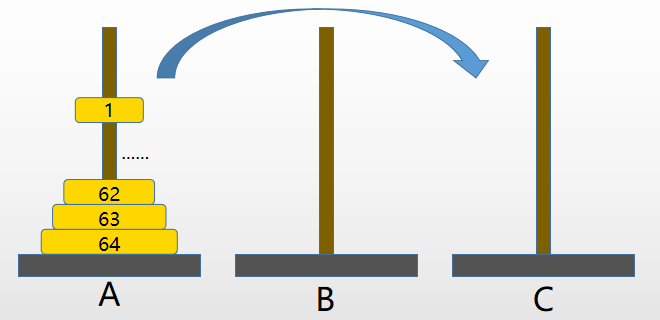
传说，在世界中心贝拿勒斯（在印度北部）的圣庙外有左中右三根足够长的柱子（塔）

左边柱子上套着 64 片金片，金片按“上小下大”排，其余两根是空柱子

僧人们借助中间的柱子将左边柱子上的金片移动到右边……

(2) 要求

• 一次只能移动一片
• 金片之间，必须是上小下大，即大金片不能放到小金片上
• 借助中间柱子，将左边柱子上所有的金片都移到右边柱子为止

(3) 程序

# 使用递归

def hanoi(n, a, b, c):
    """
    n：塔的层数
    a：左边的塔
    b：中间的塔
    c：右边的塔
    """

    if n == 1:
        print(a, '-->', c)		# 将 a 塔顶层金片移到 c 塔
    else:
        hanoi(n-1, a, c, b)		# a 塔的 n-1 层金片借助 c 塔移到 b 塔
        print(a, '-->', c)		# 将 a 塔剩下的那一层金片移到 c 塔
        hanoi(n-1, b, a, c)		# b 塔的 n-1 层金片借助 a 塔移到 c 塔

    return None

hanoi(64, 'A', 'B', 'C')		# A 塔的 64 层金片借助 B 塔移动到 C 塔

• 非递归解法详见 [Python3 练习] 006 汉诺塔2 非递归解法