<知识整理>2019清北学堂提高储备D2

简单数据结构：

　　一、二叉搜索树

　　1、前置技能：

　　　　　　n/1+n/2+……+n/n=O(n log n）  （本天复杂度常涉及）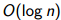

　　2、入门题引入：

　　　　

　　　　N<=100000.

　　　　这里多了一个删除的操作，因此要将所有的数都记录下来维护。一个个枚举很容易超时，这时就到了二叉搜索树显示本领的时候了。

　　　　

　　　　

　　　　（注：子树节点的key值小/大于这个点，即子树中所有的节点的key值都小/大于这个点。同时不考虑有两个节点key值相等的情况）

　　　　　　实例：

　　　　　　

　　　　

　　　　

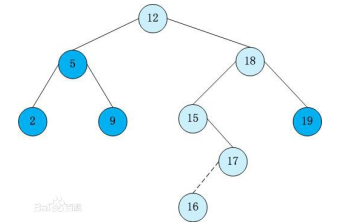
　　　　　　1、查询最大/小值：

　　　　　　　　

　　　　　　　　最大值自然就是往右儿子走啦。

　　　　　　　　核心代码（最小值）：

　　　　　　　　

 int FindMin()
 {
     int x=root;
     while(ls[x]) x=ls[x];
     return key[x];
 }

　　　　　　2、插入一个值：

　　　　　　

　　　　　　核心代码：

　　　　　　

 void insert(int val) {
     key[+ + tot] = val;
     ls[tot] = rs[tot] = ;
     int now = root;//当前访问的节点为now.
     for(; ;) {
         if (val < key[now])
             if (!ls[now]) ls[now] = x, fa[x] = now, break;
             else now =ls[now];
         else if (!rs[now]) rs[now] = x, fa[x] =now, break;
             else now = rs[now];
     }
 }

　　　　　　3、删除一个值

　　　　　　

　　　　　　代码：

　　　　　　

 int Find(int x)
 {
     int now = root;
     while(key[now]! = x)
     if (key[now] < x) now = rs[now]; else now = ls[now];
     return now;
 }

　　　　　　　

　　　　　　　　设y是x右子树中所有点里，权值最小的点，则y必没有左儿子。找这个点可以从x先走一下右儿子，再走一下左儿子。找到y后，把y的右子树接到y的父节点上（必为其左子树），再用y覆盖掉x就行了。　　

　　　　　　　　

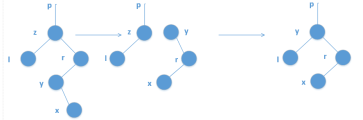
　　　　　　代码：

　　　　　　　　

//(由于不需要求每个节点的子树大小，在相应的代码前打上的注释号）
void del(int x)//删除一个值为x的点
{
        int id=Find(x),t=fa[id];//找到这个点的编号
        if (!ls[id]&&!rs[id])
        {
                if (ls[t]==id) ls[t]=; else rs[t]=; //去掉儿子边
    //            for (i=id;i;i=fa[i]) size[i]--;
        }
        else
        if (!ls[id]||!rs[id])
        {
                int child=ls[id]+rs[id];//找存在的儿子的编号
                if (ls[t]==id) ls[t]=child;
                else rs[t]=child;
                fa[child]=t;//让父亲认自己儿子为儿子，自己受到冷淡
    //            for (i=id;i;i=fa[i]) size[i]--;
        }
        else
        {
                int y=rs[id]; while (ls[y]) y=ls[y]; //找y
                if (rs[id]==y) //y正好是这个点的右儿子，则直接替代它（篡位…）
                {
                        if (ls[t]==id) ls[t]=y; else rs[t]=y;
                        fa[y]=t;
                        ls[y]=ls[id];
                        fa[ls[id]]=y;
                    //    for (i=id;i;i=fa[i]) size[i]--;
                    //    size[y]=size[ls[y]]+size[rs[y]];//y的子树大小需要更新
                }
                else //最复杂的情况
                {
                    //    for (i=fa[y];i;i=fa[i]) size[i]--;//注意到变换完之后y到root路径上每个点的size都减少了1
                        int tt=fa[y]; //先把y提出来
                        ls[tt]=rs[y];
                        fa[rs[y]]=tt;              //再来提出x
                        if (ls[t]==x)
                        {
                            ls[t]=y;
                            fa[y]=t;
                            ls[y]=ls[id];
                            rs[y]=rs[id];
                        }
                        else
                        {
                            rs[t]=y;
                            fa[y]=t;
                            ls[y]=ls[id];
                            rs[y]=rs[id];
                        }
                //        size[y]=size[ls[y]]+size[rs[y]]+1;//更新一下size
                }
        }
}

　　　　　　　　（这么长的代码吓我一跳）

　　　　　4、

　　　　　　

　　　　　　（注：子树长度包括该子树的根）

　　　　　　代码：

　　　　

 int Findkth(int now, int k)//当前根节点     “第k大”的k
 {
     if (size[rs[now]] >= k) //第k大在右子树
         return Findkth(rs[now], k);
     else
         if (size[rs[now]] +  == k) //当前即为第k大
             return key[now];
         else //第k大在左子树，由于递归后要不受递归前右子树的影响，递归进去的k进去时对递归前的整体而言，进去后只对递归后的整体而言，
              //因此k应减去递归前右子树和根节点的数目
             return Findkth(ls[now], k - size[rs[now]] - );
 }

　　　　　　5、遍历：

　　　　　　

　　　　　　　　代码：

　　　　　　　　

　　　　　让我们回到最初的题。
　　　　　　一个良好的例子（数据）:3 1 2 4 5（3层深的树）
　　　　　　一个糟糕的例子（数据）:1 2 3 4 5（5层深的树）
　　　　　　二叉搜索树每次操作访问O(h)个节点。

　　　　　　（故建树时可先sort一遍，以中间点为根，这样深度基本就位logn级别的了）

　　　　　　

　　二、二叉堆

　　　　https://www.cnblogs.com/InductiveSorting-QYF/p/10776293.html（曾经写过，安利一下，在这里就只写写新东西吧）　

　　　　堆没有二叉搜索树的性质，即左边的不一定比右边的小。堆只满足儿子与父亲的关系，因此常常用来搞最大/最小值。　　

　　　1、建堆：

　　　　　　除了一个个插入以外，还有一个时间复杂度相差不大（稍慢一点）、很便捷的方法：直接sort排下序。

　　　2、查询最大/最小值：大/小根堆的堆顶就是啦。

　　　3、插入删除：详见链接。

　　　4、修改一个点的权值（以小根堆为例）：变小往上浮，变大往最小的儿子的方向下潜（交换）

　　　应用：堆排序（详见链接）

　　　　例题：　　

　　　　　1、丑数

　　　　　

　　　　　　题解：

　　　　　　考虑构造小根堆。

　　　　　　

　　　　EX:　　

　　　　　

　　　　　　　　(注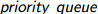：：优先队列，跟堆差不多。默认大根堆，改成小根堆一是可以重载小于号成大于号的功能（感觉怪怪的），而是在定义的类型后加上“vector<类型>，greater<类型>  ”（注意最后有空格，否则右移运算符警告））

　　　　　　　Q.push(x)插入一个元素
　　　　　　　Q.top()访问堆顶
　　　　　　　Q.pop()删除一个
　　　　　　　Q.clear() 清空

　　　　

　　　　深入学习：https://blog.csdn.net/byn12345/article/details/79523516

　　　　　　浅谈：set可看做集合，内部实际上采用红黑树。有两个特点：1、自动排序。2、每个元素只会出现一次（即没有值相等的两个元素出现在同一个set中）

　　　　　　　　功能函数：

　　.insert(x)            ,向容器插入元素x

　　.erase(x) 　　　,删除容器中的元素x

　　.begin()     　　 ,返回set容器第一个元素的迭代器

　　.end() 　　　　 ,返回一个指向当前set末尾元素的下一位置的迭代器.

　　.clear()   　　     ,删除set容器中的所有的元素

　　.empty() 　　　,判断set容器是否为空

　　.max_size() 　 ,返回set容器可能包含的元素最大个数(set的最大容量）

　　.size() 　　　　 ,返回当前set容器中的元素个数

　　.find() 　　　　,

　　　　　　　　注:访问set容器中的元素应在指向该元素的迭代器前加“*”（星号）

　　　　　　　　　　　　声明迭代器：    set<类型>::iterator 名字;  注：迭代器只支持++和--两种运算。

三、区间RMQ问题

　　

显然在1000000规模的询问下，显然O(n)算法必定超时了。引入一个数据结构：

总结：ST表预处理较慢，询问快速（区间小而询问多更明显），但几乎只能求求最大/小值

代码如下： 1 //代码以求区间最大值为例

 int i,j,m,n,p,k,ST[K+][N],a[N],Log[N];

 int Find(int l,int r)
 {
         int x=Log[r-l+];
         return max(a[r],max(ST[x][l],ST[x][r-(<<x)+])); //注意到对于[l,r],[l,l+2^x-1],[r-2^x+1,r]并起来是[l,r]
 }

 int main()
 {
         scanf("%d",&n);
         for (i=;i<=n;++i) scanf("%d",&a[i]);
         for (i=;i<=n;++i) ST[][i]=a[i];//本身
         for (i=;i<=K;++i)
             for (j=;j+(<<i)-<=n;++j)//这里i与j的意义与上文相反
                     ST[i][j]=max(ST[i-][j],ST[i-][j+(<<(i-))]); //ST[i][j]为从j开始的长度为2^i的区间的最大值
                                                         //显然[j,j+2^i)=[j,j+2^(i-1))+[j+2^(i-1),j+2^i)=max(ST[i-1][j],ST[i-1][j+2^(i-1)])
         for (i=;(<<i)<N;++i) Log[<<i]=i; //令Log[x]为比x小的最大的2^y
         for (i=;i<N;++i) if (!Log[i]) Log[i]=Log[i-];
         printf("%d\n",Find(,));//以[1,3]为例
 }

　　　　　　当我们要更改一个值时，要把所有覆盖到这个值的区间全部更改，而ST表中重叠的区间有很多，拖长时间复杂度。所以

　

引入一个数据结构：线段树：

　　注意到线段树的结构有点像分治结构,深度也是O(logN)的

　　核心操作：区间拆分:

　　　　我们可以将一个区间[a,b]拆分成若干个节点,使得这些节点代表的区间加起来是[a,b],并
且相互之间不重叠.(节点尽可能少、区间不重叠，降低复杂度）
　　　　所有我们找到的这些节点就是”终止节点”.

　　区间拆分的步骤

　　　　从根节点[1,n]开始，考虑当前看的节点表示的是[L,R].
　　　　如果[L,R]在所拆分的区间[a,b]之内,那么它就是一个终止节点.
　　　　否则,分别考虑[L,Mid],[Mid + 1,R]与[a,b]是否有交,递归两部分中有交的继续找终止节点.

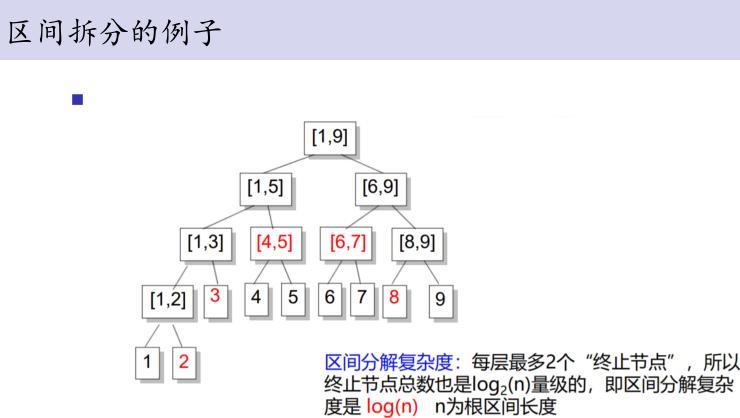
　　　　时间复杂度浅谈：易知区间拆分时每层最多有2个节点要递归下去为4个节点，4个节点中又最多有2个节点需要继续往下递归，故时间复杂度为O(log n)，不过常数有点大。

　　　　区间拆分解题方法：

　　　　代码如下：

 //以区间最大值为例

 #define ls (t*2)
 #define rs (t*2+1)
 #define mid ((l+r)/2)

 using namespace std;

 int i,j,m,n,p,k,add[N*],sum[N*],a[N],ans,x,c,l,r;

 void build(int l,int r,int t)//线段树初始化
 {
         if (l==r) sum[t]=a[l];
         else
         {
              build(l,mid,ls);
              build(mid+,r,rs);
              sum[t]=max(sum[ls],sum[rs]); //预先处理区间[l,r]的最大值
         }
 }

 void modify(int x,int c,int l,int r,int t) //将a[x]修改为c,然后需要对所有包含x的区间进行更新
 {
         if (l==r) sum[t]=c; //只有一个点的时候可以直接计算
         else
         {
                 if (l<=x&&x<=mid) modify(x,c,l,mid,ls);
                 else modify(x,c,mid+,r,rs);
                 sum[t]=max(sum[ls],sum[rs]);//回溯的时候[l,mid],[mid+1,r]的答案已经算出，可以利用两个儿子进行更新
         }
 }

 void ask(int ll,int rr,int l,int r,int t) //询问[ll,rr]这个区间的最大值,l,r,t表示的是当前线段树上位置代表的区间[l,r]和编号t
 {
         if (ll<=l&&r<=rr) ans=max(ans,sum[t]); //找到了一个完整被[ll,rr]区间包含的区间,直接把答案记进去
         else
         {
                 if (ll<=mid) ask(ll,rr,l,mid,ls); //如果和左儿子有交就往左儿子走
                 if (rr>mid)  ask(ll,rr,mid+,r,rs);  //如果和右儿子有交就往右儿子走
         }
 }

　　

　　　　题解：

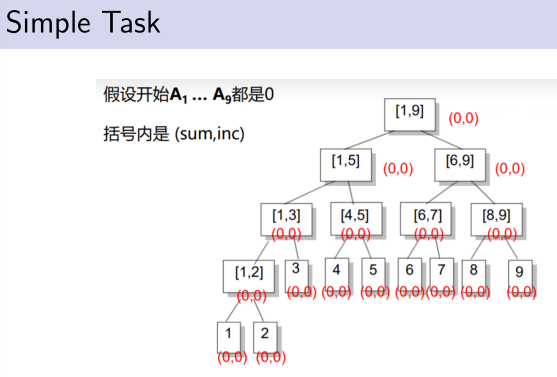
　　　　对于每个节点[L,R],我们记录A _L + ... + A _R .

　　　　对于操作1:相当于我们对[i,i]这个区间做了一个区间分解.更新它并更新沿路找[i,i]时经过的所有祖先节点.
　　　　对于操作2:我们对[L,R]做一个区间分解,将每个终止节点区间对应的和累加起来就是想要知道的区间和.

　　　　

　　题解：

　　　　如果只用之前的方法，进行操作1就要访问所有要加的节点，显然要凉凉。考虑多记录一个值inc,表示这个区间被整体的加了多少.

引入一个新思想：

　　　　 

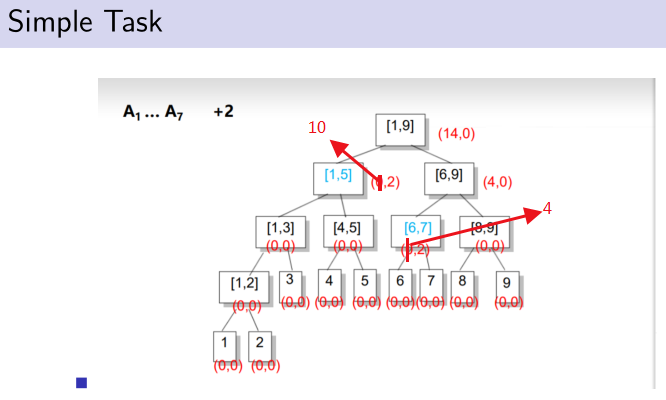
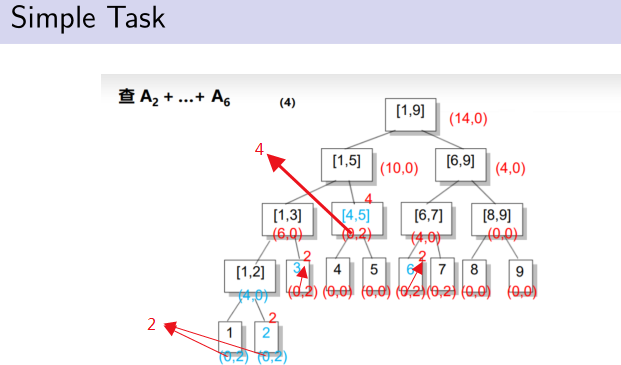
　　　　　　不会，因为后来的可覆盖先来的，而题目正让我们求最后来的。

　　(注：只要是一个起点与它前一个不同、终点与它后一个不同的子段就是一个不同段。）

　　树状数组https://blog.csdn.net/qq_39553725/article/details/76696168（感觉外面的大佬写的很好）：

　　　　求lowbit：

　　　　记f i 是i的最低位。若i是奇数,f i = 1,否则f i = f i/2 * 2。（f i/2相当于f i左移一位）

　　　　好麻烦啊，有没有更简便的算法？

　　　　有！：lowbit(i) = i& − i

　　　　　　引用一个证明：

首先明白一个概念，计算机中-i=（i的取反+1），也就是i的补码 
而lowbit，就是求（树状数组中）一个数二进制的1的最低位，例如01100110，lowbit=00000010；再例如01100000，lowbit=00100000。 
所以若一个数（先考虑四位）的二进制为abcd，那么其取反为(1-a)(1-b)(1-c)(1-d)，那么其补码为(1-a)(1-b)(1-c)(2-d)。 
如果d为1，什么事都没有；但我们知道如果d为0，而二进制每一位又不能是2，于是就要进位。如果c也为0，那么1-b又要加1，然后又有可能是1-a……直到碰见一个取反后为0的bit才不会继续进位，我们假设这个bit的位置为x 
这个时候可以发现：是不是x高位的补码都与其自身不同？，x低位的补码与其自身一样都是0？ 同时x位一定是1。
例如01101000，反码为10010111，补码为10011000，可以看到在原来数往右数第五位前，补码的进位使第五位为最低位的1，更低位全为0，与原码一样，只有在这个数处，0+1=1，连锁反应停止，同时该位的最高位都与原码相反，所以这个数的lowbit此时就可用and（&）确定了。

　　　

　　　　

　　看不懂？

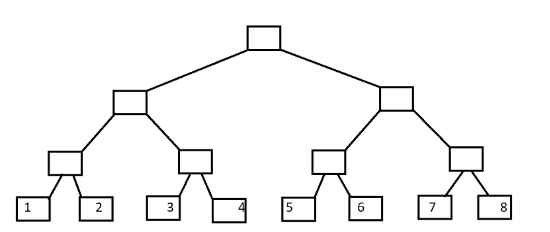
这个可看懂了吧。

（好像也只能解决这些问题了。当然世界上不缺乏充满想象力的出题人。）

　

（转载自大佬博客）

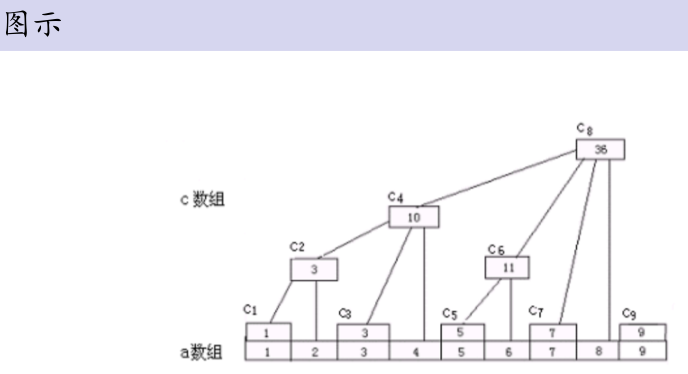
　　一个简单的总结证明：前i项的和即为a[1]+a[2]+…a[i]，而c[i]=c[i-lowbit[i]+1]+c[i-lowbit[i]+2]+…+c[i],令i=i-lowbit[i],继续往下算c[i]就行。

　　用前缀和相减的方法即可求区间和。

　　实际上单点更新就是区间查询的逆过程。

　　时间复杂度：

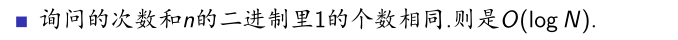
四、并查集

　　尝试硬维护，发现如果元素是新输入的，则就要进行一次搜索，时间复杂度肯定不行。

　　引入一个新数据结构：并查集

　　核心操作：

　一段操作示例：

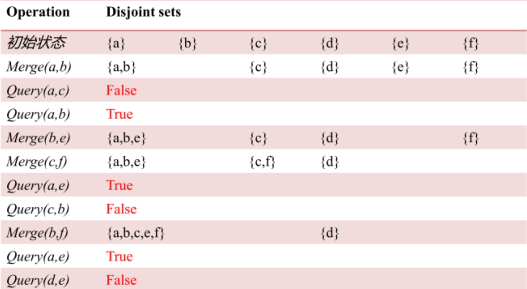
　　1.合并Merge

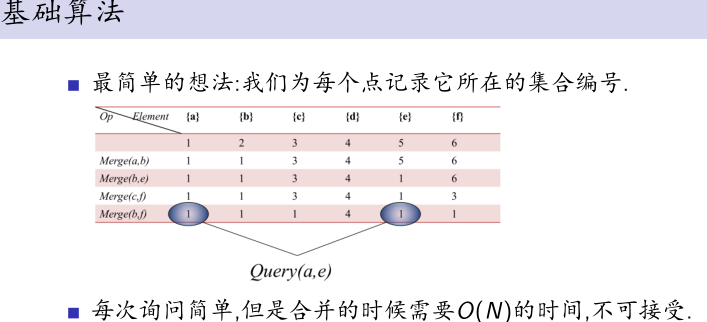
　　　　　　每次把数量小的并到大的上，可以做到O(N logN),这样还需要记录每个集合有哪些点,非常麻烦.

　　　　

　　

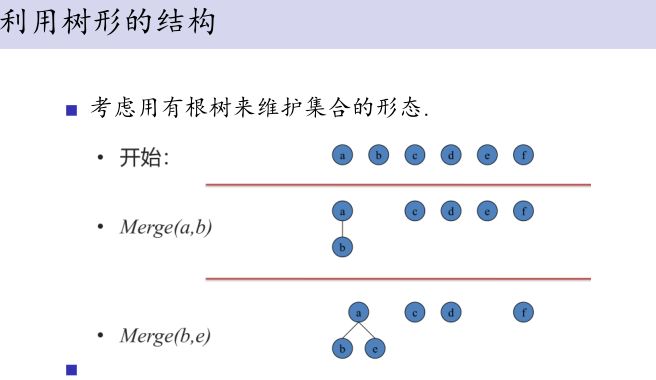
（俗称找爸_爸）

　　　　　　1、路径压缩（简称认儿_子）：
　　　因为各种操作都是看某节点的最终祖先，而跟这个节点本身并没有什么关系。因此可以在getroot递归返回的过程中顺便让节点直接指向它的最终祖先，这样下次在查询的时候查询路径就缩短很多。查询n个点的时间复杂度O（nlogn）

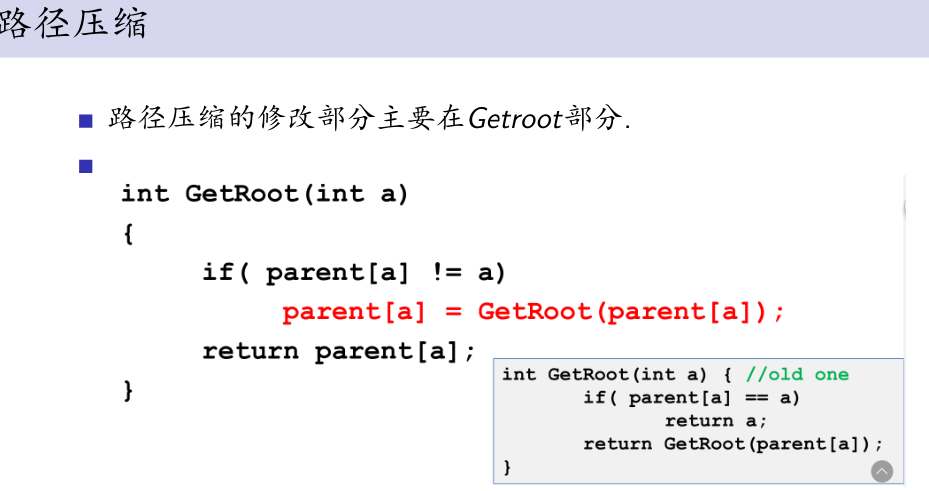
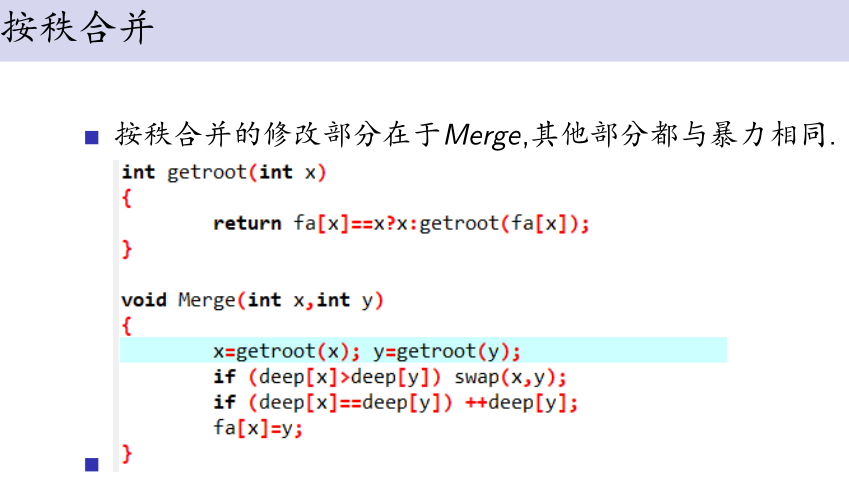
　　　　　　2、按秩（高度）合并

　　　　　　对每个顶点，再多记录一个当前整个结构中最深的点到根的深度deep _x .

　　　　　　注意到两个顶点合并时,如果把比较浅的点接到比较深的节点上.

　　　　　　如果两个点深度不同，那么新的深度是原来较深的一个.

　　　　　　只有当两个点深度相同时，新的深度是原来的深度+1.　　

　　　　　　当每个点都按此规则合并时，deep_i=x的点下至少有2^x个，又因为总共有N的点，所以x至多为log₂n，故每次查询向上找的路径最长为logn.查询n个点的时间复杂度O（nlogn）

　　　　　　

例题：

1、

离散化：https://blog.csdn.net/weixin_43061009/article/details/82083983

2、

　　题解：只要两个团队中有同一个人，那么这个人就可以将两个团队连接成一个团队。因此不用考虑一个人分别属于几个不同的团队，直接按照普通并查集的思路做就可。

　　　　小提示：当有多组数据待测时不要忘记清零。

　　　　　　　　　　~十二省联考命题组温馨提醒您：数据千万条，清空第一条；多测不清空，暴零两行泪。（来自十二省联考2019）