python 数据结构之二分查找的递归和普通实现

二分查找就是待查找的列表进行分半搜索

如下所示

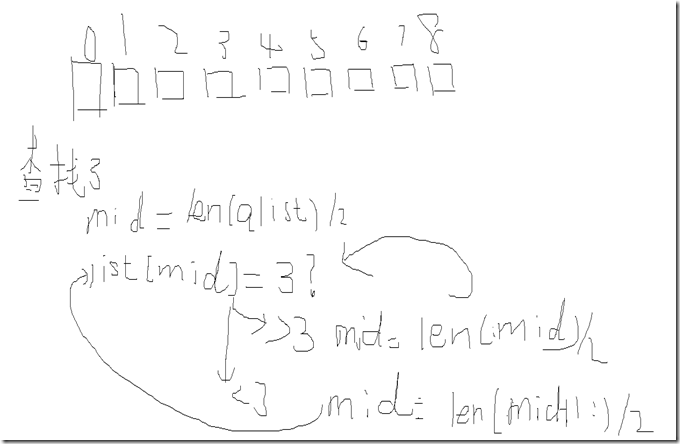
二分查找普通实现：

def erfen(alist, item):
    start = 0
    end = len(alist) - 1
    while start <= end:
        n = int((start + end) / 2)
        if alist[n] == item:
            return True
        elif alist[n] > item:
            end = n - 1
        else:
            start = n + 1
    return False

alist = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
print(erfen(alist,10))
print(erfen(alist, 3))

递归实现：

#import sys
#sys.setrecursionlimit(1000000)
"""解决maximum recursion depth exceeded error """

def erfen(alist,item):
    if len(alist) == 0:
        return False
    else:
        mid=int(len(alist)/2)
        if alist[mid] == item :
            return True
        elif item < alist[mid]:
            return erfen(alist[:mid],item)
        else :
            return erfen(alist[mid+1:],item)

alist = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
print(erfen(alist,10))
print(erfen(alist, 3))