FHQ Treap摘要

原理

以随机数维护平衡，使树高期望为logn级别

不依靠旋转，只有两个核心操作merge（合并）和split（拆分）

因此可持久化

先介绍变量

 const int N=;
 int n;
 struct Node {
     int val,key,siz;                                                                //权值，随机权值，子树大小
     int son[];                                                                        //左右儿子（0左1右）
     void res() {                                                                    //清空该节点（用于删除）
         son[]=son[]=siz=val=key=;
     }
 } tree[N];
 int ins;
 int mem[N],inm;                                                                    //内存回收池
 int root;

var

核心操作

merge并返回合并后的根

假设有两颗子树x，y，且x的所有节点的值都小于y的所有节点的值，随机权值都以小根堆的形式存储。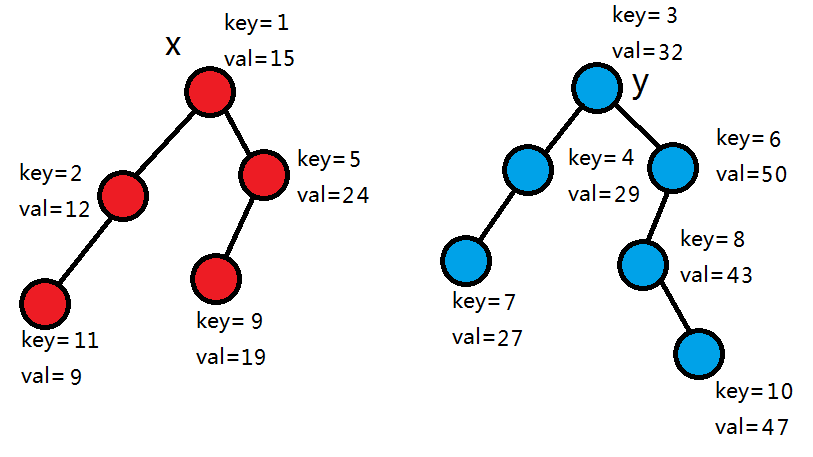

此时要合并x和y。我们先比较它们的根的随机权值，发现1<3，则x的左子树全部不变，让右子树继续和y合并。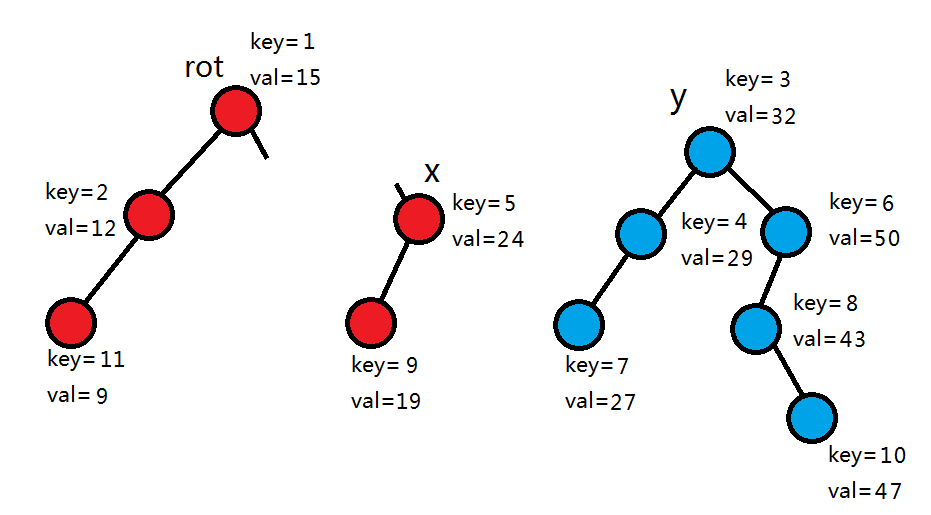

这时我们发现，5>3，所以y作为rot的右儿子，y的右子树全部不变，让y的左子树继续和x合并。

由于5>4，所以y和y的右子树作为rot的左儿子，y的左子树继续和x合并。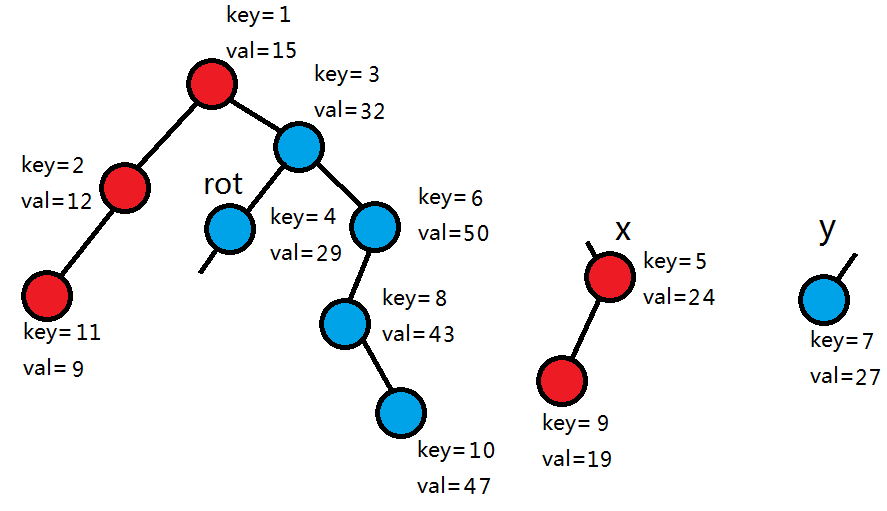

5<7，所以接入x和它的左子树作为rot的左儿子。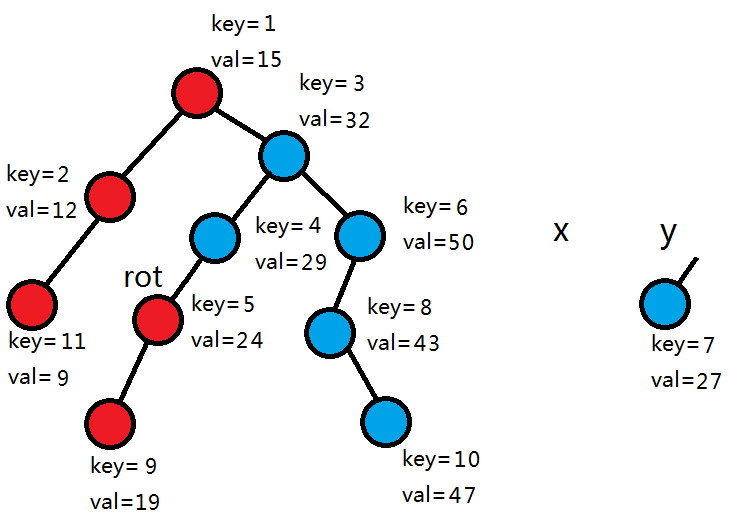

发现此时x为0，所以直接返回y，合并结束。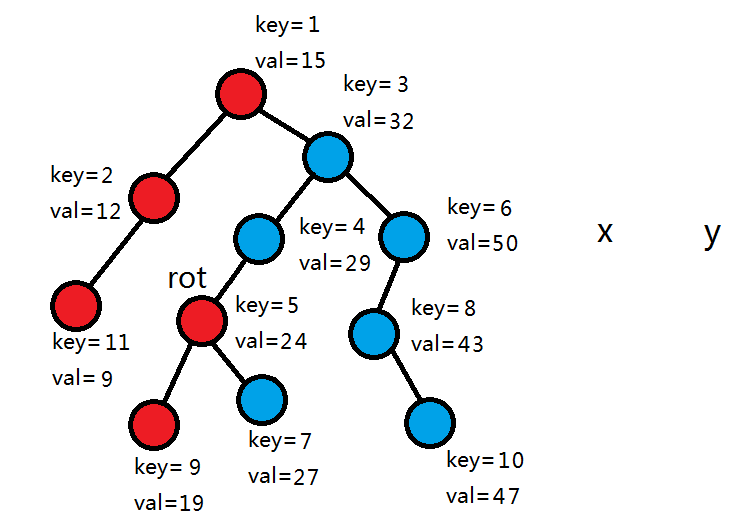

 int merge(int x,int y) {                                                            //合并两棵树
     if(!x||!y) return x+y;                                                            //若有一棵树为0则说明该树为空或已合并完成
     if(tree[x].key<tree[y].key) {                                                    //若x的随机权值大于y的
         tree[x].son[]=merge(tree[x].son[],y);                                        //x的右子树和y合并，返回的根作为x的右子树
         update(x);
         return x;                                                                    //返回x
     } else {
         tree[y].son[]=merge(x,tree[y].son[]);                                        //否则y的左子树和x合并，返回的根作为y的左子树
         update(y);
         return y;                                                                    //返回y
     }
 }

merge

split拆分一棵树

split有两种拆分方式，按权值拆或按排名拆。

按权值split

首先得有个基准a，即小于等于a的节点全部进入左树，大于a的节点全部进入右树。这里以a=25为例。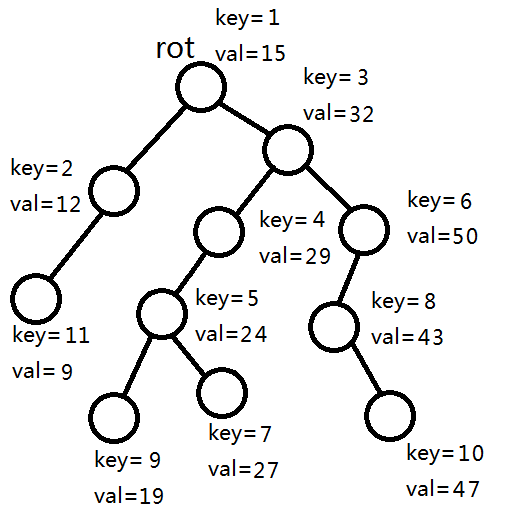

首先，发现rot的权值=15<25，由平衡树的性质可知，rot的左子树所有节点权值一定小于25，所以rot和它的的左子树全部进入左树，继续拆分rot的右子树。

32>25，所以rot和它的右子树全部进入右树，继续拆分rot的左子树。

29>25，同上。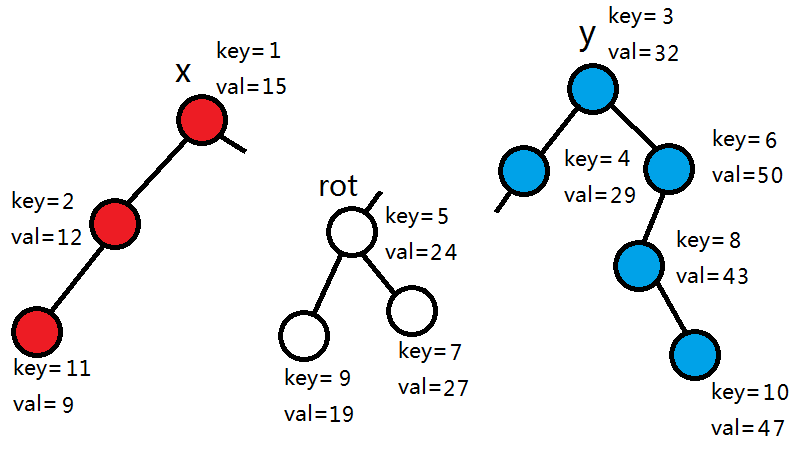

24<25，所以拆分右子树。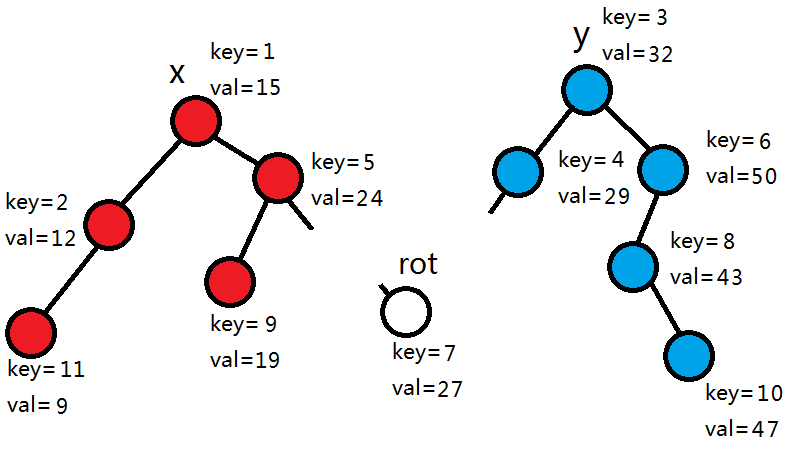

27>25，所以拆分左子树。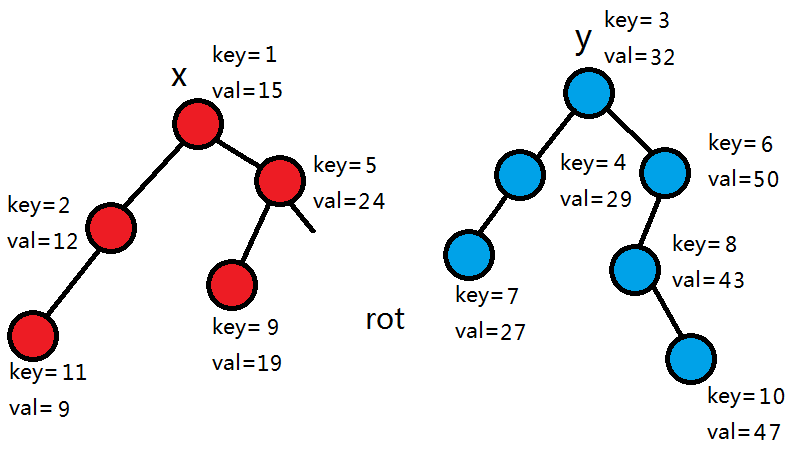

发现此时rot为0，所以拆分完毕，返回。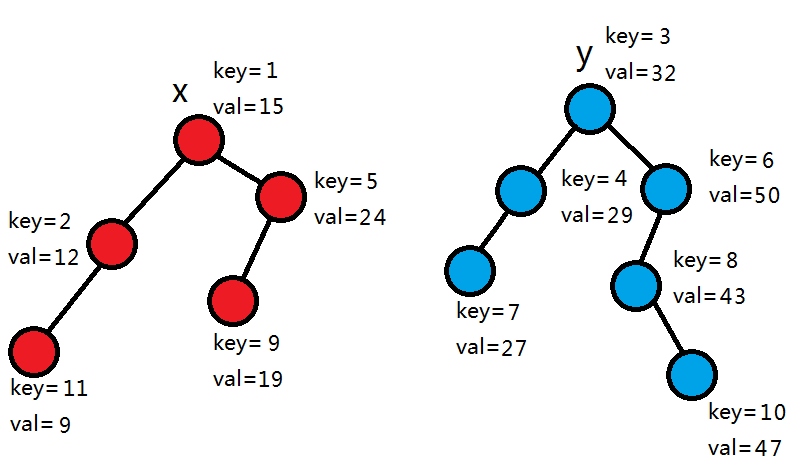

 void split1(int now,int k,int &x,int &y) {                                            //按权值拆分两颗子树（注意要用引用）
     if(!now) {                                                                        //子树为0，说明无需拆分或拆分完毕，返回
         x=y=;
         return;
     }
     if(tree[now].val<=k) {                                                            //若权值小于等于k
         x=now;
         split1(tree[now].son[],k,tree[now].son[],y);                                //拆进左树并拆分右子树
     } else {
         y=now;
         split1(tree[now].son[],k,x,tree[now].son[]);                                //否则拆进右树并拆分左子树
     }
     update(now);
 }

split1

按排名split

就是把前k个节点拆入左树，其它节点拆入右树。这里以k=5为例。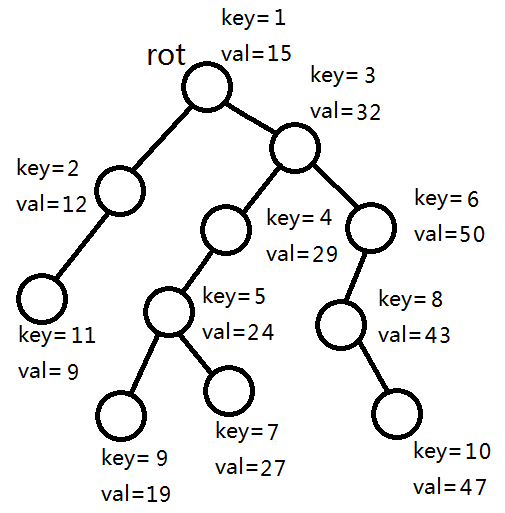

rot的左子树的siz+1=3<5，所以rot和它的左子树进入左树，其他节点拆分5-3=2个节点进入左树。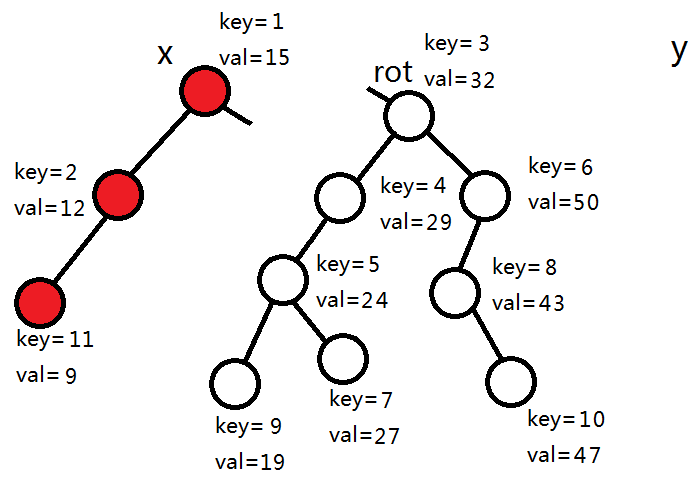

4+1>2，所以rot和右子树进入右树，其它节点继续拆分出2个节点进入左树。

3+1>2，同上。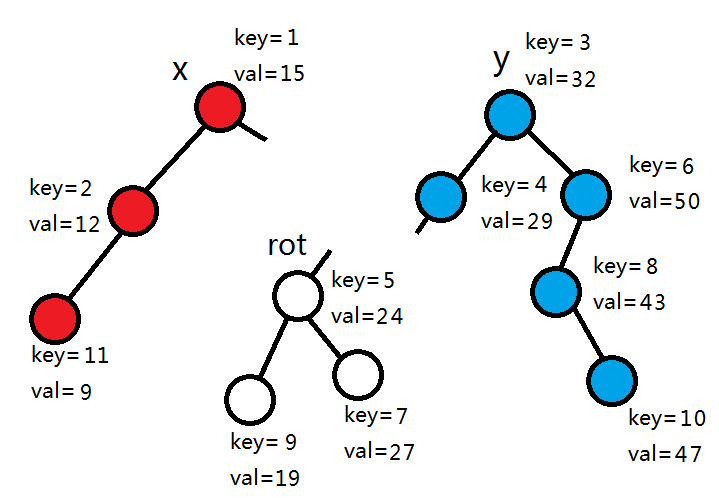

1+1=2，所以rot和左子树进入左树，其它节点继续拆分2-2=0个节点进入左树。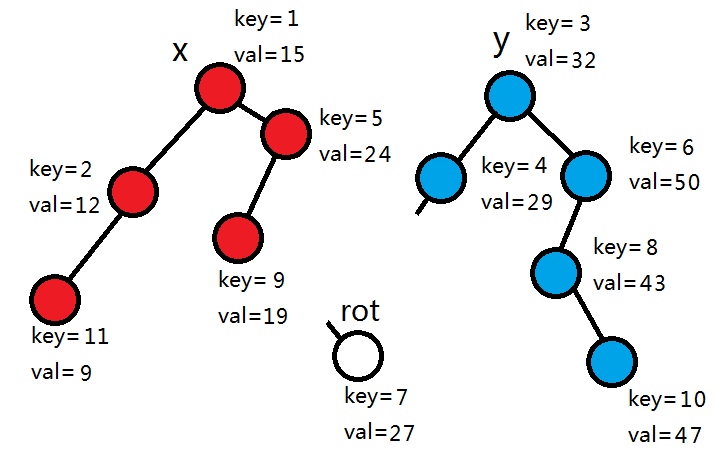

1+0>0，所以rot和右子树进入右树，其它节点继续拆分0个节点进入左树。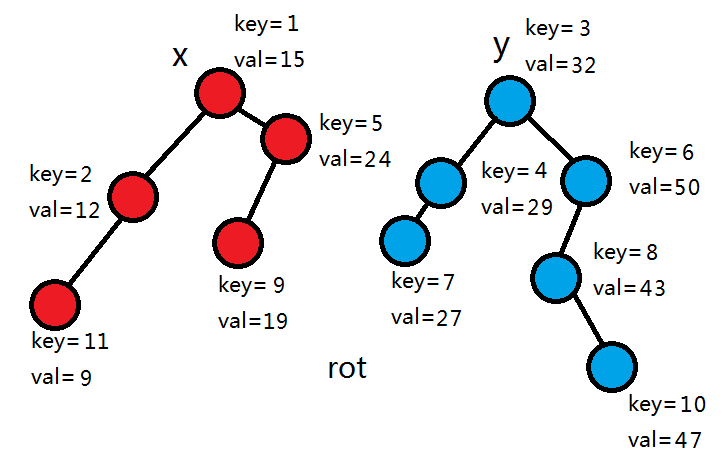

rot为0，拆分结束。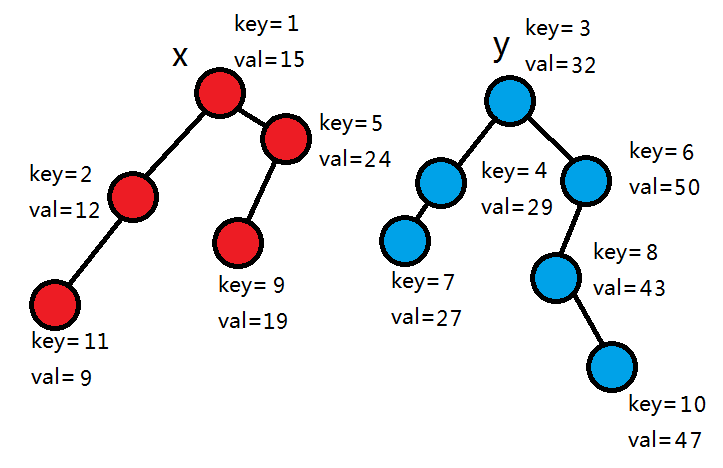

 void split2(int now,int k,int &x,int &y) {                                            //按权值拆分两颗子树（同样要用引用）
     if(!now) {                                                                        //子树为0，说明无需拆分或拆分完毕，返回
         x=y=;
         return;
     }
     update(now);
     if(k>tree[tree[now].son[]].siz) {                                                //若做子树大小+1小于等于k
         x=now;
         split2(tree[now].son[],k-tree[tree[now].son[]].siz-,tree[now].son[],y);//拆进左树并拆分右子树(注意右子树分配的名额要减少）
     } else {
         y=now;
         split2(tree[now].son[],k,x,tree[now].son[]);                                //否则拆进右树并拆分左子树
     }
     update(now);
 }

split2

其他操作

会了merge和split，其他操作就是瞎搞。

插入

插入x，先新建节点，再以x为界按权值split整棵树为a,b，再按顺序merge a，x，b。

 void insert(int x) {
     int u=(inm?mem[inm--]:++ins);                                                    //新建节点
     tree[u].key=rand();
     tree[u].val=x;
     tree[u].siz=;
     int a,b;
     split1(root,x,a,b);                                                                //split
     root=merge(merge(a,u),b);                                                        //merge
 }

insert

删除

要删除x，先将整棵树以x按权值split成a和b，再将a以x-1按权值split成c和d，则d中节点权值全为x。在d中split出排名为1的节点e和其它节点f，则e为要删的点。最后merge c，f，b。

 void delet(int x) {
     int a,b,c,d,e,f;
     split1(root,x,a,b);                                                                //split整棵树
     split1(a,x-,c,d);                                                                //将a split为c和d
     split2(d,,e,f);                                                                //将d split为e和f，则e为我们要删的节点
     mem[++inm]=e;                                                                    //回收
     tree[e].res();                                                                    //重置
     root=merge(merge(c,f),b);                                                        //merge
 }

delet

查询x的排名

先将整棵树以x-1按权值split成a和b，则a的siz+1即为x的排名。

 int finrnk(int x) {
     int a,b,c;
     split1(root,x-,a,b);                                                            //split整棵树
     c=tree[a].siz+;                                                                //a的大小就是小于x的数的个数
     root=merge(a,b);                                                                //merge
     return c;
 }

finrnk

查询第x小值

先split出整棵树前x-1小节点，则右树最小节点即为所求节点，再次split即可。

 int finnum(int &rot,int x) {
     int a,b,c,d,e;
     split2(rot,x-,a,b);                                                            //split这棵树
     split2(b,,c,d);                                                                //split出b中第1个节点
     e=tree[c].val;                                                                    //c即为第x小节点
     rot=merge(a,merge(c,d));                                                        //merge
     return e;
 }

finnum

查x前驱

将整棵树以x-1按权值split，左树中最大节点即为所求节点，转入第x小值问题。

 int las(int x) {
     int a,b,c;
     split1(root,x-,a,b);                                                            //split整棵树
     c=finnum(a,tree[a].siz);                                                        //找左树最大值
     root=merge(a,b);                                                                //merge
     return c;
 }

las

查x后继

将整棵树以x按权值split，右树中最小节点即为所求节点，转入第x小值问题。

 int nex(int x) {
     int a,b,c;
     split1(root,x,a,b);                                                                //split整棵树
     c=finnum(b,);                                                                    //找右树最小值
     root=merge(a,b);                                                                //merge
     return c;
 }

nex

时空复杂度

时间复杂度

merge、split：期望树高为logn，因此复杂度为期望O(logn)

插入、删除、查询：基于以上两种操作，复杂度期望O(logn)

常数比Treap大，但比splay小的多

空间复杂度

O(n)

例题

洛谷P3369【模板】普通平衡树

 #include<bits/stdc++.h>
 using namespace std;
 #define INF 0x7fffffff
 #define ME 0x7f
 #define FO(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout)
 #define fui(i,a,b,c) for(int i=(a);i<=(b);i+=(c))
 #define fdi(i,a,b,c) for(int i=(a);i>=(b);i-=(c))
 #define fel(i,a) for(register int i=h[a];i;i=ne[i])
 #define ll long long
 #define MEM(a,b) memset(a,b,sizeof(a))
 #define maxn (100000+10)
 int n;
 struct Node{int val,key,siz;int son[];void res(){son[]=son[]=siz=val=key=;}}tree[maxn];
 int ins,mem[maxn],inm,root;
 template<class T>
 inline T read(T &n){
     n=;int t=;double x=;char ch;
     for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());(ch=='-')?t=-:n=ch-'';
     for(ch=getchar();isdigit(ch);ch=getchar()) n=n*+ch-'';
     if(ch=='.') for(ch=getchar();isdigit(ch);ch=getchar()) n+=(ch-'')/x,x*=;
     return (n*=t);
 }void update(int x){tree[x].siz=tree[tree[x].son[]].siz+tree[tree[x].son[]].siz+;}int merge(int x,int y){if(!x||!y) return x+y;
     if(tree[x].key<tree[y].key){tree[x].son[]=merge(tree[x].son[],y);update(x);return x;}
     else{tree[y].son[]=merge(x,tree[y].son[]);update(y);return y;}
 }void split1(int now,int k,int &x,int &y){if(!now){x=y=;return;}
     if(tree[now].val<=k){x=now;split1(tree[now].son[],k,tree[now].son[],y);}
     else{y=now;split1(tree[now].son[],k,x,tree[now].son[]);}update(now);
 }void split2(int now,int k,int &x,int &y){if(!now){x=y=;return;}update(now);
     if(k>tree[tree[now].son[]].siz){x=now;
     split2(tree[now].son[],k-tree[tree[now].son[]].siz-,tree[now].son[],y);}
     else{y=now;split2(tree[now].son[],k,x,tree[now].son[]);}update(now);
 }void insert(int x){int u=(inm?mem[inm--]:++ins);
     tree[u].key=rand();tree[u].val=x;tree[u].siz=;
     int a,b;split1(root,x,a,b);root=merge(merge(a,u),b);
 }void delet(int x){int a,b,c,d,e,f;
     split1(root,x,a,b);split1(a,x-,c,d);split2(d,,e,f);
     mem[++inm]=e;tree[e].res();root=merge(merge(c,f),b);
 }int finrnk(int x){int a,b,c;split1(root,x-,a,b);c=tree[a].siz+;root=merge(a,b);return c;}
 int finnum(int &rot,int x){int a,b,c,d,e;split2(rot,x-,a,b);
     split2(b,,c,d);e=tree[c].val;rot=merge(a,merge(c,d));return e;
 }int las(int x){int a,b,c;split1(root,x-,a,b);c=finnum(a,tree[a].siz);root=merge(a,b);return c;}
 int nex(int x){int a,b,c;split1(root,x,a,b);c=finnum(b,);root=merge(a,b);return c;}
 int main(){
     read(n);
     fui(i,,n,){
         int opt,x;read(opt);read(x);
         switch(opt){
             case :insert(x);break;
             case :delet(x);break;
             case :cout<<finrnk(x)<<endl;break;
             case :cout<<finnum(root,x)<<endl;break;
             case :cout<<las(x)<<endl;break;
             case :cout<<nex(x)<<endl;break;
         }
     }
     return ;
 }

AC代码

FHQ Treap的其他作用

最重要的一点是它可以代替区间操作！而且支持可持久化！！！

区间操作

将每个点按它们的下标作为关键字，其他的像普通FHQ Treap就行了。

区间翻转的话，每次merge和split都pushdown一下。

洛谷【模板】文艺平衡树（Splay）

 #include<bits/stdc++.h>
 using namespace std;
 #define INF 0x7fffffff
 #define ME 0x7f
 #define FO(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout)
 #define fui(i,a,b,c) for(int i=(a);i<=(b);i+=(c))
 #define fdi(i,a,b,c) for(int i=(a);i>=(b);i-=(c))
 #define fel(i,a) for(register int i=h[a];i;i=ne[i])
 #define ll long long
 #define MEM(a,b) memset(a,b,sizeof(a))
 #define maxn (100000+10)
 int n,m;
 struct Node{
     int key,val;
     int siz,son[];
     char iz;
     Node(){key=val=siz=son[]=son[]=iz=;}
     Node(int x,int y){key=x,val=y,siz=,son[]=son[]=iz=;}
 }tree[maxn];
 int root;
 int l,r;
 int rnd(){static int seed=;return seed=int(seed*48271LL%(~0u>>));}
 template<class T>
 inline T read(T &n){
     n=;int t=;double x=;char ch;
     for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());(ch=='-')?t=-:n=ch-'';
     for(ch=getchar();isdigit(ch);ch=getchar()) n=n*+ch-'';
     if(ch=='.') for(ch=getchar();isdigit(ch);ch=getchar()) n+=(ch-'')/x,x*=;
     return (n*=t);
 }
 void update(int x){tree[x].siz=tree[tree[x].son[]].siz+tree[tree[x].son[]].siz+;}
 void pushdown(int x){
     if(tree[x].iz){
         tree[x].iz=;swap(tree[x].son[],tree[x].son[]);
         tree[tree[x].son[]].iz^=;tree[tree[x].son[]].iz^=;
     }
 }
 int merge(int x,int y){
     if(!x||!y) return x+y;pushdown(x);pushdown(y);
     if(tree[x].key<tree[y].key){tree[x].son[]=merge(tree[x].son[],y);update(x);return x;}
     else{tree[y].son[]=merge(x,tree[y].son[]);update(y);return y;}
 }
 void split(int now,int k,int &x,int &y){
     if(!now){x=y=;return;}pushdown(now);
     if(tree[tree[now].son[]].siz>=k){y=now;split(tree[now].son[],k,x,tree[now].son[]);}
     else{x=now;split(tree[now].son[],k-tree[tree[now].son[]].siz-,tree[now].son[],y);}
     update(now);
 }
 void dfs(int now){
     pushdown(now);
     if(tree[now].son[]) dfs(tree[now].son[]);
     printf("%d ",tree[now].val);
     if(tree[now].son[]) dfs(tree[now].son[]);
 }
 int main(){
     read(n);read(m);
     fui(i,,n,){tree[i]=(Node){rnd(),i};root=merge(root,i);}
     fui(i,,m,){
         read(l);read(r);int a,b,c;
         split(root,r,a,c);split(a,l-,a,b);
         tree[b].iz^=;
         root=merge(merge(a,b),c);
     }
     dfs(root);
     return ;
 }

AC代码

可持久化

还没折腾出来。。。最近也没时间折腾了。。。来日再说吧。。。