大叔学ML第一：梯度下降

目录

• [toc]
• 原理
• 实践一：求$y = x^2 - 4x + 1$的最小值
• 实践二：求$z = x^2 + y^2 + 5$的最小值
• 问答时间

原理

梯度下降是一个很常见的通过迭代求解函数极值的方法，当函数非常复杂，通过求导寻找极值很困难时可以通过梯度下降法求解。梯度下降法流程如下：



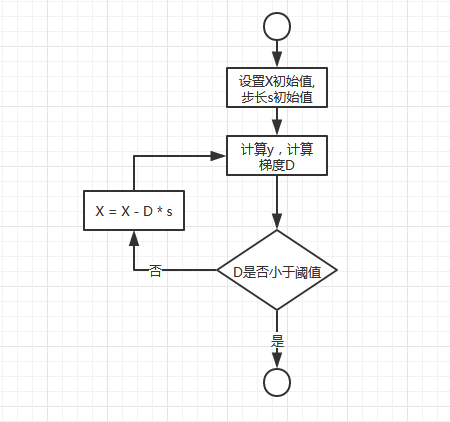
上图中，用大写字母表示向量，用小写字母表示标量。

假设某人想入坑，他站在某点，他每移动一小步，都朝着他所在点的梯度的负方向移动，这样能保证他尽快入坑，因为某个点的梯度方向是最陡峭的方向（实际上，梯度下降法有时候不是最快的下降方向，比如我们下山时，可能前方遇到一个梁，跨过去是最快的下山方式，而不是绕开，如果是梯度下降法，肯定会绕开。），如下图所示，此图画的不太能表达这个观点，但是懒得盗图了，意会吧：

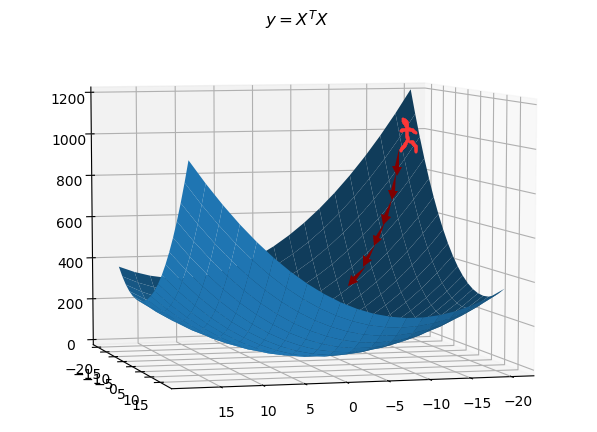
以下举两个例子，两个例子中的被求函数都很简单，其实直接求导算极值更好，此处仅用来说明梯度下降法的步骤。

实践一：求\(y = x^2 - 4x + 1\)的最小值

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt

def descent(p, original_x = 50, steplength = 0.01):
    ''' gradient descent, return min y '''

    deriv = p.deriv(m = 1) # 多项式p的导函数
    Y = [] # 保存每次迭代后的y值，方便绘图
    count = 0 # 迭代次数
    x = original_x # 设置x初始值
    d = deriv(x) # x位置的导数
    threshold = 0.001 # 阈值，当梯度小于此值时停止迭代

    while np.abs(d) > threshold:
        x = x - d * steplength
        y = p(x)

        Y.append(y)
        count += 1
        d = deriv(x)

    plt.plot(np.arange(1, count + 1), Y)
    plt.show()
    return y

if __name__ == "__main__":
    p = np.poly1d([2, -4, 1])
    min_y = descent(p)
    print(min_y)

把迭代数和对应的函数值绘制出来以查看迭代效果：

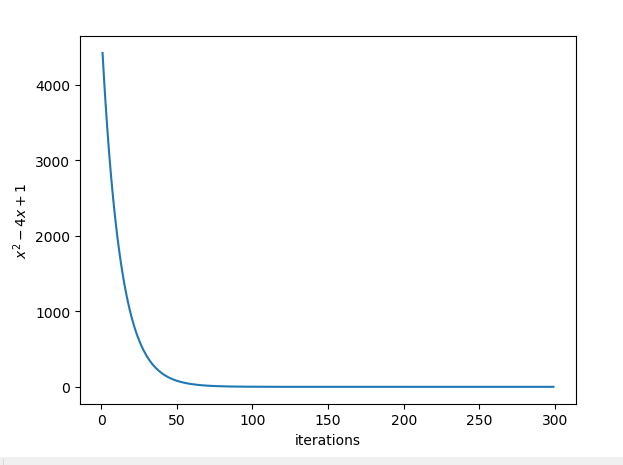
实践二：求\(z = x^2 + y^2 + 5\)的最小值

以下代码中，把一组x和y当成一个向量处理，即\(z = X^TX + 5\)，其中\(X=[x\ y]^T\)

import numpy as np
import matplotlib.pyplot as plt

def deriv(xy):
    dxy = 2 * xy
    return dxy

def descent(xy, steplength = 0.01):
    ''' gradient descent, return min y '''

    d = deriv(xy) # x^2 + y^2 + 5的梯度
    Y = [] # 保存每次迭代后的y值，方便绘图
    count = 0 # 迭代次数
    threshold = 0.001 # 阈值，当梯度的模小于此值时停止迭代

    while np.linalg.norm(d) > threshold:
        xy = xy - d * steplength
        y = np.dot(xy, xy) + 5

        Y.append(y)
        count += 1
        d = deriv(xy)

    plt.plot(np.arange(1, count + 1), Y)
    plt.show()
    return Y[-1]

if __name__ == "__main__":
    y = descent(np.array([50, 50]))
    print(y)

把迭代数和对应的函数值绘制出来以查看迭代效果：

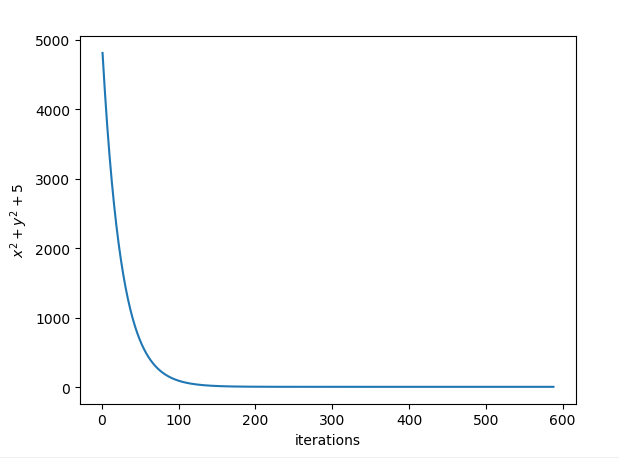
问答时间

Q：无法收敛到某个足够小的函数值，最后报错： overflow ...

A：步长设置太大，步子大了，容易跨过最低点，导致函数值在最低点上下震荡或发散，如图：



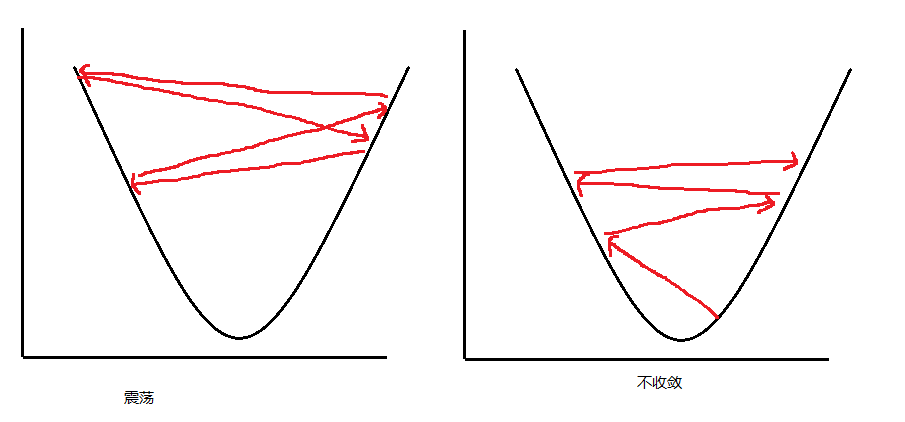
可以人为设置迭代次数（而不是通过阈值控制是否继续迭代），然后观察函数值是否收敛：

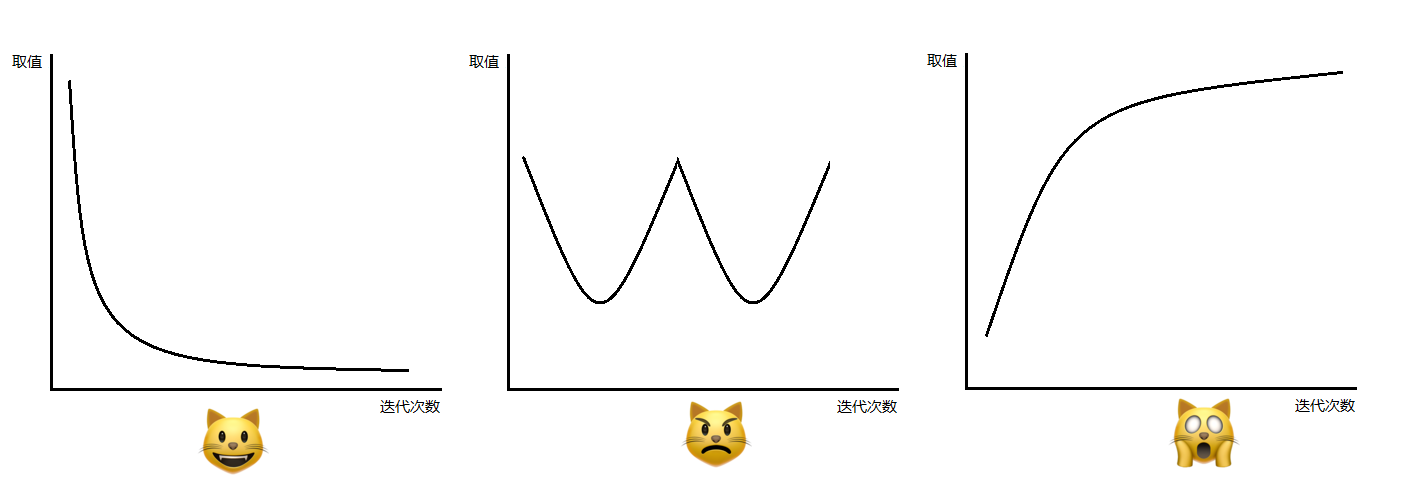
Q：如何选择合适的步长

A：步长太大会导致函数值不收敛，步长太小又浪费性能，可以通过绘制如上面的迭代次数和函数值关系图，刚才结果后调整步长，尽量选择满足需求的最大步长。达爷在他的网课中给出的建议是：按照这样的序列试验步长：..., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, ...。通过算法自动预测步长十分复杂，非大叔所能为。

Q：何时停止迭代？

A：可设定一个阈值，当梯度的模长小于这个阈值时停止迭代（当函数接近极值时，梯度接近0）。也可以人为通过刚才迭代次数和函数值图像设定迭代次数。

Q：是否还有其他迭代法？

A：还有牛顿法和拟牛顿法，和梯度下降法的区别是牛顿法不是沿着梯度负方向下降的，而是另一套算法得出的方向，下降速度更快。

Q：迭代法是否一定会找到函数值域内的最小值？

A：不是，如果函数不是一个凸函数，那么迭代法可能会找到一个局部最小值或鞍点值。

Q：函数最大值怎么找

A：给函数取个负号然后找最小值，或者沿着梯度方向前进而不是负梯度方向前进