最大二位子数组和问题(homework-02)

　　前面已经谈过最大一维子数组和问题，这里面扩展到二维。

一. 常规情况

一个矩形的数组，找到一个矩形的子数组有最大的元素和，求这个和。

　　1. 从朴素算法入手，枚举矩形数组的4个顶点，以此计算其数组和。同样，时间复杂度很大，我们仅以此入手逐步优化。

2. 参照一维数组的思路，保存中间结果，利用动态规划优化算法。优化点就是子数组求和一处，二维数组的求和不同于一维，但是仍然能找到方法：

先声明这个方法是参考《编程之美》书中的讲解的，鄙人大脑迟钝，尚无法独创：

令二维数组的起点不是0，而是1，使用PS[i][j]表示以[0][0], [i][0], [0][j], [i][j]四个顶点围起来的子数组和，边界上的PS[*][0]和PS[0][*]全置零。则有：

PS[i][j] = PS[i - 1][j] + PS[i][j - 1] - PS[i - 1][j - 1] + A[i][j]

其中，A为整个二维数组，Row_num, Clm_num分别为数组行数、列数。

void cal_PS(){
    int i, j;
    for (i = 0; i <= Row_num; i++){
        PS[i][0] = 0;
    }
    for (j = 0; j <= Clm_num; j++){
        PS[0][j] = 0;
    }
    for (i = 1; i <= Row_num; i++){
        for (j = 1; j <= Clm_num; j++){
            PS[i][j] = PS[i - 1][j] + PS[i][j - 1] - PS[i - 1][j - 1] + A[i][j];
        }
    }
}

上面的函数处理了部分和，这部分时间复杂度O(Row_num² * Clm_num²).

3. 有了部分和，下面寻找最大和的数组。我们的核心思路是把未知问题归结到已知的一维问题上。即，首先循环二维子数组数组的上下界，在每个上下界确定的情况下，用一维数组的方法确定其左右边界。形象一点说，就是先假定数组上下界已知，然后把每一列上的元素压扁，变成一维的。BC(a, c, j)就是a, c两行之间第j列元素加在一起的和。

核心代码如下：

 int MaxSum_mode1(int isCalled){
     if(isCalled == ){ //有时候不需要读取文件，见后文
         readArray(file);
         cal_PS();
     }
     int maximum = -;
     int Start, All;
     for (int a = ; a <= Row_num; a++){//起始行
         for (int c = a; c <= Row_num; c++){ //终结行
             Start = BC(a, c, Clm_num); //下面就是阐述的算法
             All = Start;
             for (int i = Clm_num - ; i >= ; i--){
                 if(Start < )
                     Start = ;
                 Start += BC(a, c, i);
                 if(Start > All)
                     All = Start;
             }
             if(All > maximum)
                 maximum = All;
         }
     }
     return maximum;
 }

至此，我们完成了新问题的求解和优化，时间复杂度 O(Row_num² * Clm_num)

下面的动图展示了BS扫描的部分，左上角表示当前的All值：

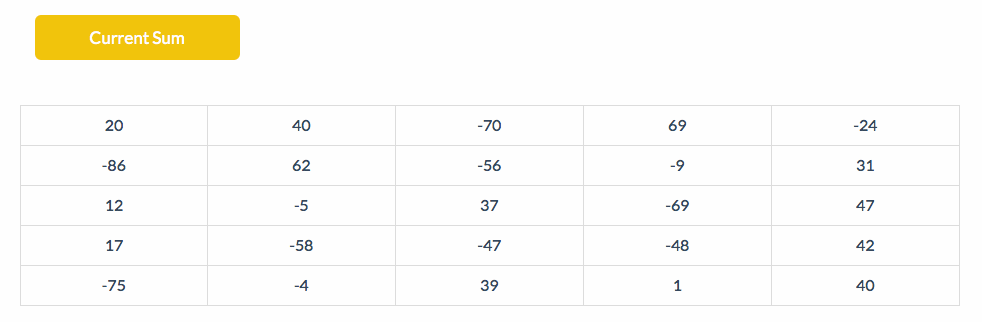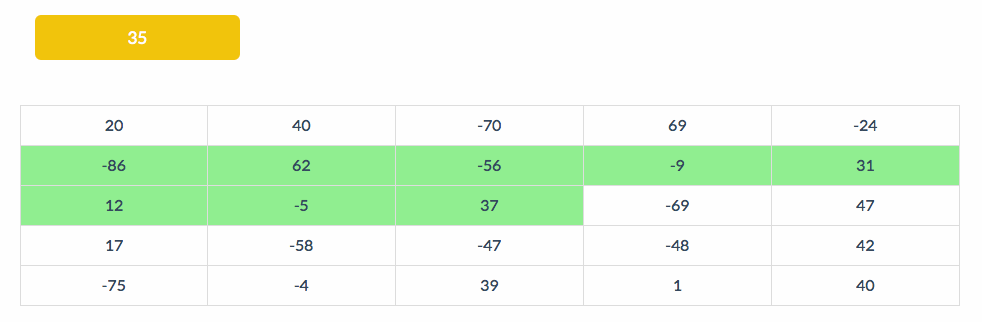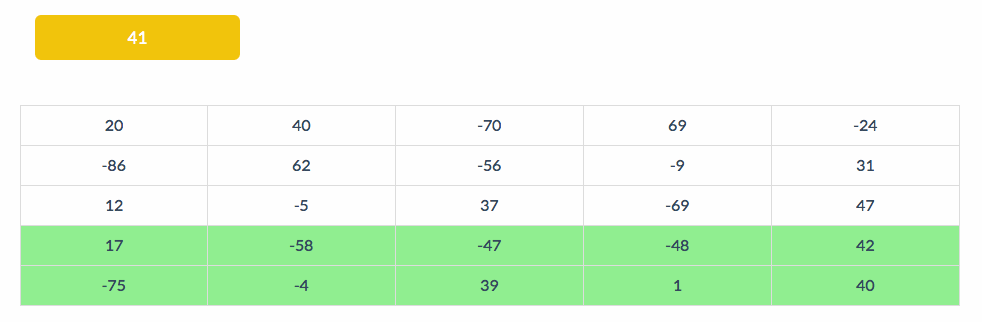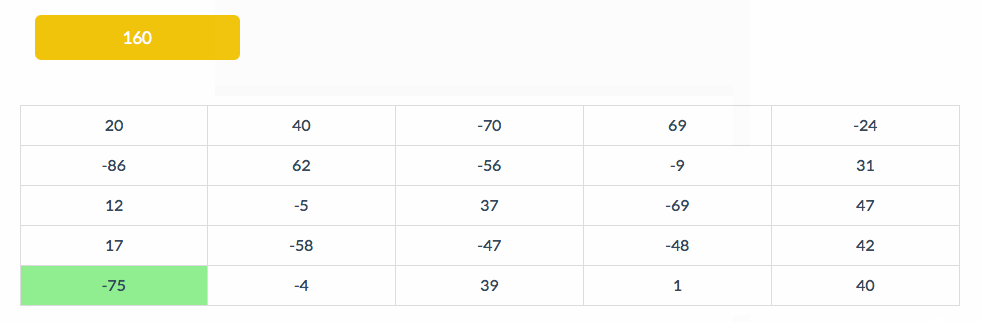
二. 拓展模式

这里面我们进行两种拓展：二维数组水平方向收尾相接成环，和竖直方向相接成环。

　　1. /h 模式，水平成环

冷静的分析这种拓展造成了什么不同，我们发现拓展之后，问题仅是原始问题+新情况而已。如果最大和子数组不是跨越边界拼接在一起的情况，那就和上面的老问题相同；另一种情况就是，最大和子数组是跨越边界拼接在一起的。这种情况，即子数组分为A[1][*]~A[i][*], A[j][*]~A[Clm_num-1][*]两段，跨越边界接在一起。其中A[1][*],A[Clm_num-1[*] 分别是数组的左右边界那列。

换一句话说，假设a,c上下界已经固定，第二种情况就是从全局内剔除中间一段留下两边。被剔除的要求和小于0，且最小。接下来的问题就转化为求中间部分的子数组的最小值了。故，分两种情况讨论，取大值为最终答案。第二种情况就是修改第一种情况而来。注意求和部分。

 int MaxSum_mode3(int isCalled){ // /h
     if(isCalled == ){
         readArray(file);
         cal_PS();
     }
     int MaxSum_noJump = MaxSum_mode1(); // 不跨越的和最大子数组
     int MaxSum_Jump; //跨越的和最大子数组

     int minimum = ;
     int Start, All;
     int WholeSum = ;
     int tmpSum = ;
     for (int a = ; a <= Row_num; a++){//起始行
         for (int c = a; c <= Row_num; c++){ //终结行
             tmpSum = ;
             Start = BC(a, c, Clm_num - );
             All = Start;
             for (int i = Clm_num - ; i > ; i--){
                 if(Start > )
                     Start = ;
                 Start += BC(a, c, i);
                 if(Start < All)
                     All = Start;
                 tmpSum += BC(a, c, i);//累加去除头尾后的 中间元素的和
             }
             if(All <= minimum){
                 int newSum = tmpSum + BC(a, c, ) + BC(a, c, Clm_num) + BC(a, c, Clm_num - );
                 if (newSum - All > WholeSum - minimum){
                     minimum = All;
                     WholeSum = newSum; //当找到更小的 中间元素的和，重新算a,c两行之间全部元素的和
                 }
             }
         }
     }
     MaxSum_Jump = WholeSum - minimum; //有跨越情况，子数组分头尾两半。两半的和等于全部元素和 减 中间踢出去的元素和的小于零的最小值
     return MaxSum_noJump > MaxSum_Jump ? MaxSum_noJump : MaxSum_Jump;
 }

下面的动图展示了BS扫描的步骤。左上角显示的是All的值：　　

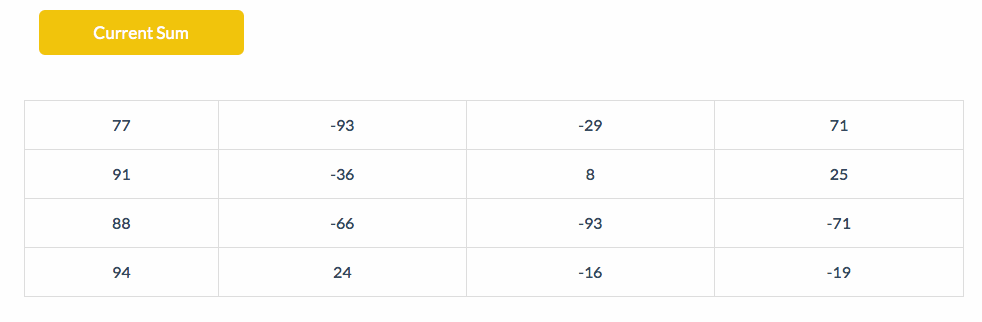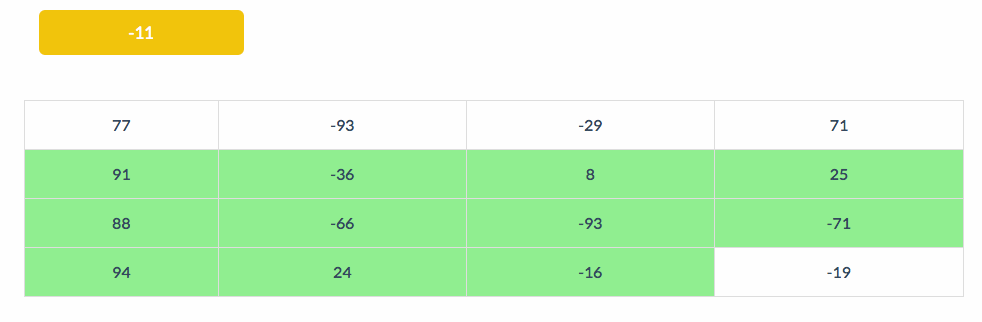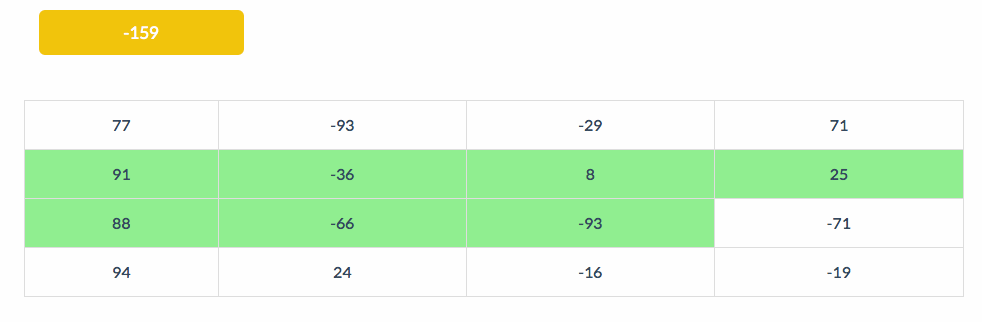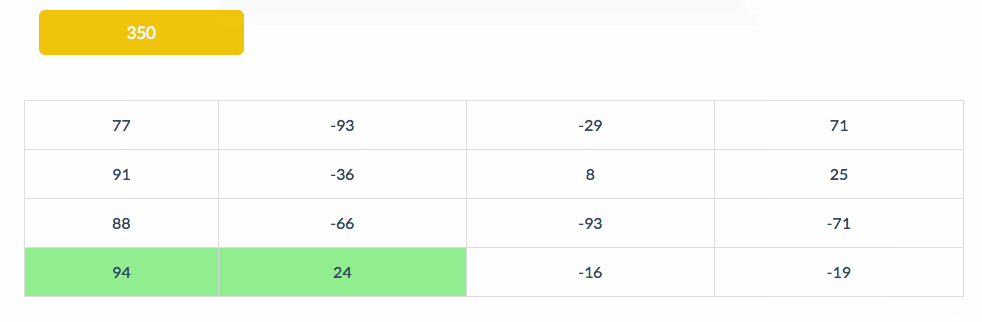
2. /v 模式，竖直成环。

到目前，我们一直坚守“归结法”的思想，在简单问题找到优化解法后，将新问题化归到老问题，同样，/v的情况也不例外。在读取文件时，我们将数组存储成与前面沿对角线对称的形式，就可以利用水平成环的解法而不做任何改动。因为调换后的新数组的水平方向就是原来的竖直方向。下面只需要展示读文件存数组时的步骤即可：

 for (i = ; i <= Row_num; i++){
         for (j = ; j <= Clm_num; j++){
             A[i][j] = fgint(file);           //这里仅需换成A[j][i]即可
         }
     }

　　3. /h /v 模式，将二维数组变成轮胎形状。

这个笔者确实想了很久。受前面启发，依旧分情况讨论，以运用归结法化简。轮胎形状，首先考虑最大子数组不是竖直、水平均跨越的情况，细分为3种情况，即前文三种情况。第四种情况我们专门来讨论，即最大和子数组两个方向均跨越。数组的形状就是二维数组的四个角。

这里我们的思路是，仿照前面的思路，a表示左上、右上两块子数组的下界，c表示下面两块子数组的上届，在假定a，c已知的情况下，在原数组中删去a, c之间的行，新的子数组将被接成上下连续、左右分开的形状，这正好是之前处理过的水平相接成环的情况。因此，这部分的代码为：

 int MaxSum_mode5(){ // /h /v
     readArray();
     cal_PS();
     int Max_md1 = MaxSum_mode1();
     int Max_md3 = MaxSum_mode3();
     int Max_md4 = MaxSum_mode4();
     swap(&Clm_num, &Row_num); //  /v情况颠倒了数组，这里还原行、列数目
     int Max_md5;

     Max_md5 = -;
     int a, c, tmp = Max_md5;
     for (a = ; a < Row_numB; a++){
         for (c = a; c < Row_numB; c++){
             makeA(a, c); //删去数组a,c行之间的行（含a, c
             tmp = MaxSum_mode3();
             if (tmp > Max_md5){
                 Max_md5 = tmp;
             }
         }
     }
     if(Max_md1 > Max_md5)
         Max_md5 = Max_md1;
     if(Max_md3 > Max_md5)
         Max_md5 = Max_md3;
     if(Max_md4 > Max_md5)
         Max_md5 = Max_md4;
     return Max_md5;
 }

三. 以上的总结

描述在这么多相似的需求面前, 你怎么维护你的设计 (父类/子类/基类, UML, 设计模式,  或者其它方法) 让整个程序的架构不至于崩溃的?

程序的核心在于算法，因此并未使用面型对象的方法。为使得代码易于维护，且在归结法密集使用的本程序中，我通过将程序模块化增加的扩展性和可维护性。这具体表现在单独功能独自成函数，在能够使用已完成函数的情况下，调用函数而非重写代码。上述从mode1到mode5，后面的模式均使用了前面的模式的代码。

给出你做单元测试/代码覆盖率的最终覆盖率的报告, 用截屏显示你的代码覆盖率

首先给出上述各情况的测试截屏。从下图可以看到测试用例、模式和结果。

/h /v的测试，通过调试发现各个情况的值都正确，故可证明程序正确。

阅读 工程师的能力评估和发展 和相关文章, 在完成作业的时候记录自己花费的时间, 并填下表。如果你对有些术语不太清楚，请查看教材和其它资料。如果你认为你不需要做某个步骤, 那就跳过去。

	Personal Software Process Stages	时间百分比(%)	实际花费的时间 (分钟)	原来估计的时间 (分钟)
Planning	计划
·         Estimate	·         估计这个任务需要多少时间，把工作细化并大致排序	230%	700	300
Development	开发
·         Analysis	·         需求分析 (包括学习新技术)	100%	60	60
·         Design Spec	·         生成设计文档（博客）	100%	90	90
·         Design Review	·         设计复审 (和同事审核设计文档)	0	0	0
·         Coding Standard	·         代码规范 (制定合适的规范)	0	0	0
·         Design	·         具体设计	150%	240	360
·         Coding	·         具体编码	100%	180	180
·         Code Review	·         代码复审	100%	30	30
·         Test	·         测试（自我测试，修改代码，提交修改）	100%	60	60
Reporting	总结报告
Test Report 测试报告		（博客）
Size Measurement 计算工作量 Postmortem & Improvement Plan 事后总结, 并提出改进		100%	40	40
Total	总计	220%	总用时 约11小时	总估计的用时 5小时

你在这个作业中学到了什么?  有什么好的设计值得分享?  感想如何 (太容易 / 太难 / 太无趣)?

本次作业中，我深入体会了“归结法”的思想，也为自己独自从学习到思考最后解决问题而愉快。因为之前较少接触这样算法类的问题，也没有这样专业而完整的开发过程，本次作业让我学会了如何学习、如何思考问题，并在完成后总结。当然，我也有不足，就是deadline之前没能抓紧时间，导致最后的任务量异常繁重。编程序不能等deadline，是我应该明白的道理。

至于好的设计，我已经尽力写出能想到的最好的了...当然我还会继续欣赏其他高分同学的作品并学习。上面的设计，也是受《编程之美》一书和很多人的博客启发而想到的。

这次作业的感想是，过程很充实，让人学到很多，但是任务量有点大... 因为个人选的课程有点多，所以不得不在国庆节坐到腰酸背疼..也许熟练了能好点吧..

四. 其他

关于/a的情况.. 没有什么好算法，只好用退火随机化算法了，没什么能分享的了。

然后关于“单元测试”，“代码覆盖率”，因为本程序应对5种模式，代码覆盖率会比较低。因为没采用面向对象的类，暂时未找到代码覆盖率的查看方法，我会下节课请教助教大人或者老师的。

为了便于理解，上面的代码并不是最终的代码。程序不断扩充，代码也有少许变化。

感谢阅读，祝中秋快乐！