双向BFS

转自“Yuan”

如果目标也已知的话，用双向BFS能很大提高速度

单向时，是 b^len的扩展。

双向的话，2*b^(len/2)  快了很多，特别是分支因子b较大时

至于实现上，网上有些做法是用两个队列，交替节点搜索 ×，如下面的伪代码：

while(!empty())

{

扩展正向一个节点

遇到反向已经扩展的return

扩展反向一个节点

遇到正向已经扩展的return

}

但这种做法是有问题的，如下面的图：

 

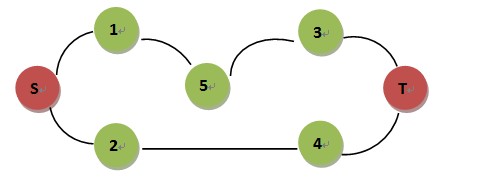
求S-T的最短路，交替节点搜索（一次正向节点，一次反向节点）时

Step 1 : S –> 1 , 2

Step 2 : T –> 3 , 4

Step 3 : 1 –> 5

Step 4 : 3 –> 5   返回最短路为4，错误的，事实是3，S-2-4-T

正确做法的是交替逐层搜索，保证了不会先遇到非最优解就跳出，而是检查完该层所有节点，得到最优值。 也即如果该层搜索遇到了对方已经访问过的，那么已经搜索过的层数就是答案了，可以跳出了，以后不会更优的了。 当某一边队列空时就无解了。

优化：提供速度的关键在于使状态扩展得少一些，所以优先选择队列长度较少的去扩展，保持两边队列长度平衡。这比较适合于两边的扩展情况不同时，一边扩展得快，一边扩展得慢。如果两边扩展情况一样时，加了后效果不大，不过加了也没事。