[HDU 4828] Grids

Grids

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 562    Accepted Submission(s): 223

Problem Description

　　度度熊最近很喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。他想把1到2N这些数依次放进去，但是为了使格子看起来优美，他想找到使每行每列都递增的方案。不过画了很久，他发现方案数实在是太多了。度度熊想知道，有多少种放数字的方法能满足上面的条件？

 

Input

　　第一行为数据组数T(1<=T<=100000)。
　　然后T行，每行为一个数N(1<=N<=1000000)表示长方形的大小。

 

Output

　　对于每组数据，输出符合题意的方案数。由于数字可能非常大，你只需要把最后的结果对1000000007取模即可。

 

Sample Input

2
1
3

 

Sample Output

Case #1:
1
Case #2:
5

 

Hint

对于第二组样例，共5种方案，具体方案为：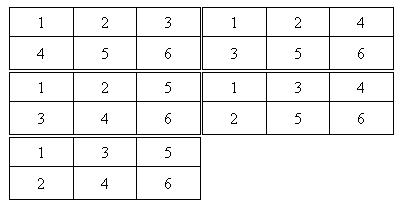

 

Source

2014年百度之星程序设计大赛 - 初赛（第一轮）

 

逆元、

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define ll long long
#define N 1000010

int dp[N];

int exgcd(int a,int b,int& x, int& y)
{
    if(b==)
    {
        x=;
        y=;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
int inv(int a,int MOD)
{
    int x,y;
    exgcd(a,MOD,x,y);
    x=(x%MOD+MOD)%MOD;
    return x;
}
void init()
{
    int MOD=;
    dp[]=;
    dp[]=;
    for(int i=;i<=N-;i++)
    {
        dp[i]=( (ll)dp[i-]*(*i-)%MOD * (ll)inv(i+,MOD))%MOD;
    }
}
int main()
{
    init();
    int T,n,iCase=;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        printf("Case #%d:\n%d\n",iCase++,dp[n]);
    }
    return ;
}