最小生成树------Prim算法

　　定义:设G=(V,E)是一个无向连通图。如果G的生成子图T=(V,E’)是一棵树，则称T是G的一棵生成树(Spanning Tree)。

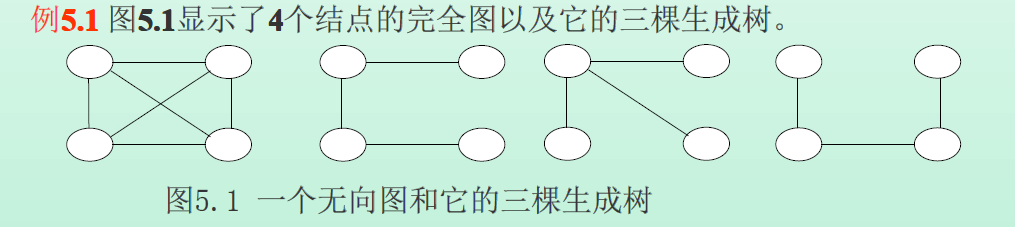
　　应用生成树可以得到关于一个电网的一组独立的回路方程。第一步是要得到这个电网的一棵生成树。设B是那些不在生成树中的电网的边的集合，从B中取出一条边添加到这生成树上就生成一个环。从B中取出不同的边就生成不同的环。把克希霍夫(Kirchoff)第二定律用到每一个环上，就得到一个回路方程。用这种方法所得到的环是独立的(即这些环中没有一个可以用那些剩下的环的线性组合来得到)，这是因为每一个环包含一条从B中取来的边(生成树固定的情况下)，而这条边不包含在任何其它的环中。因此，这样所得的这组回路方程也是独立的。可以证明，通过一次取B中的一条边放进所产生的生成树中而得到的这些环组成一个环基，从而这图中所有其它的环都能够用这个基中的这些环的线性组合构造出来。

　　生成树在其它方面也有广泛的应用。一种重要的应用是由生成树的性质所产生的，这一性质是，生成树是G的这样一个最小子图T，它使得V(T)=V(G)且T
连通并具有最少的边数。任何一个具有n个结点的连通图都必须至少有n-1条边，而所有具有n-1条边的n结点连通图都是树。如果G的结点代表城市，边代表连接两个城市的可能的交通线，则连接这n个城市所需要的最少交通线是n-l条。G的那些生成树代表所有可行的选择。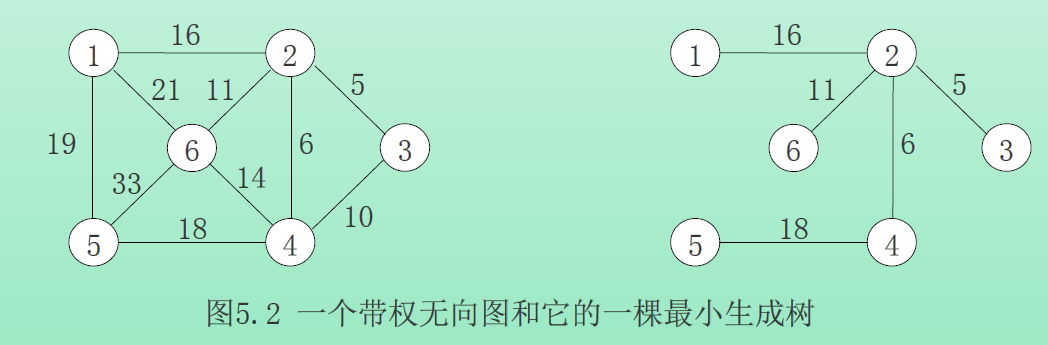

下面举个例子具体说明：

Prim最小生成树算法
line void Prim(edge[],COST[][],int n,&T[][],int minCOST) {

//edge()是G的边集。COST(n,n)是n结点图G的成本邻接矩阵，矩阵元素COST(i,j)是一个正实数，如果不存在边(i,j)，则为+∞。计算一棵最小生成树并把它作为一个集合存放到数组T(1..n-1,2)中。(T(i,1)，T(i,2))是最小成本生成树的一条边。最小成本生成树的总成本最后赋给minCOST。

 float COST[n,n]；float minCOST；
 int near[]，n，i，j，k，m，T[n-][]；
 (k,m) = 具有最小成本的边；
 minCOST=COST(k,m)；
 (T(,),T(,)) = (k,m)
 for(i=；i=n；++i) {//将near置初值
 if(COST(i,m)<COST(i,k)) near[i]=m；
 else { near[i]=k；}；//if
 }；//for
 near[k]=near[m]=

 for(i=；i<=n-；++i) { //找T的其余n-2条边
 设j是near(j)≠0且COST[j][near[j]]最小的下标
 (T(i,),T(i,))=(j，near[j])；
 minCOST = minCOST + COST[j][near[j]]；
 near[j]=；
 for(k=；k<=n；++k) { //修改near
 if((near[k]!= && COST[k][near[k]])＞COST[k][j])
 {near[k]=j；
 }；//if
 }；//for
 }；//for
 if(minCOST)→∞) { print(‘no spanning tree’)}；//if
 }//Prim

　　函数过程Prim所需要的时间是Θ(n2)，其中n是图G的结点数。具体分析如下：第3行花费Θ(e) 时间,其中e=|E|。而第4行花费Θ(1)时间；第6～9行的循环花费Θ(n)时间；第12行和第16～20行的循环要求Θ(n)时间，因此第11～21行的循环的每一次选代要花费Θ(n)时间。所以这个循环的总时间是Θ(n2)。故过程Prim有Θ(n2)的时间复杂度。

　　因为最小生成树包含了与每个结点v相关的一条最小成本边，因此还可以把这算法稍许加快一点。为此，假设T是图G=(V,E)的最小成本生成树。设v是T中的任一结点。又设(v,w)是所有v相关的边中具有最小成本的一条边。假定(v,w)不属于E(T)，且对于所有的边(v,x)∈E(T)，COST(v,w)＜COST(v,x)。把(v,w)包含到T中就生成一个唯一的环。这个环必定包括一条边(v,x)，x≠w。从E(T) ∪{(v,w)}中去掉边(v,x)就破坏了这个环而且没有使图(v,E(T)∪｛(v,w)｝-｛(v,x)｝)不连通，因此该图也是一棵生成树。由于COST(v,w)<COST(v,x)，所以这棵生成树比T有更小的成本。这与T是G中最小成本生成树相矛盾。故T包含如上所述的那样的最小成本边。