[codeforces821E]Okabe and El Psy Kongroo

题意：(0,0)走到(k,0),每一部分有一条线段作为上界，求方案数。

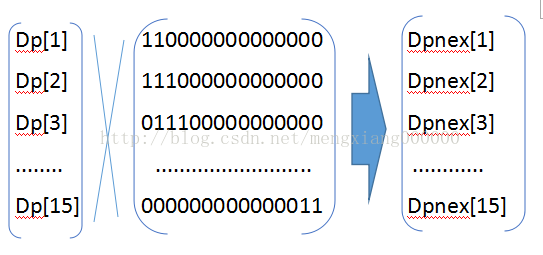
解题关键：dp+矩阵快速幂，盗个图，注意ll

关于那条语句为什么不加也可以，因为我的矩阵C，就是因为多传了了len的原因，其他位置都是0，所以不需要加

 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<iostream>
 using namespace std;
 typedef long long ll;
 const ll mod=1e9+;
 struct mat{
     ll m[][];
 }A;

 mat mul(mat &A,mat &B,ll len){
     mat C={};
     for(int i=;i<=len;i++){
         for(int k=;k<=len;k++){
             for(int j=;j<=len;j++){
                 C.m[i][j]=(C.m[i][j]+A.m[i][k]*B.m[k][j]%mod+mod)%mod;
             }
         }
     }
     return C;
 }

 mat mod_pow(mat A,ll n,ll len){
     mat B={};
     for(int i=;i<=len;i++) B.m[i][i]=;
     while(n>){
         if(n&) B=mul(B,A,len);
         A=mul(A,A,len);
         n>>=;
     }
     return B;
 }

 int main(){
     ll n,k;
     ios::sync_with_stdio();
     cin.tie();
     cout.tie();
     for(int i=;i<;i++){
         int j=i->=?i-:;
         for(;j<=i+&&j<;j++){
             A.m[i][j]=;
         }
     }
     mat C;
     cin>>n>>k;
     mat B={};
     B.m[][]=;
     ll cnt=;
     for(int i=;i<n&&cnt<k;i++){
         ll a,b,c;
         cin>>a>>b>>c;
         if(b>k) b=k;
         cnt+=b-a;
         C=mod_pow(A, b-a, c);
         B=mul(B, C, c);
         for(ll j=c+;j<;j++) B.m[j][]=;//这句话不加也可以，为什么？
     }
     cout<<(B.m[][]+mod)%mod<<"\n";
     return ;
 }