luogu4151 最大XOR和路径

然后呢这道题其实很简单

我们先考虑一种简单的情况，从1直接走到n(不管怎么走的，反正就是走) 然后就能找到一个路径了

这个走的过程用各种zmj算法都能过

然后呢我们发现如果直接走基本不会得到最优解，考虑模拟退火

考虑增广

一个增广方法是，从某一个点开始走到一个环，在环上走一圈，然后原路返回，如图

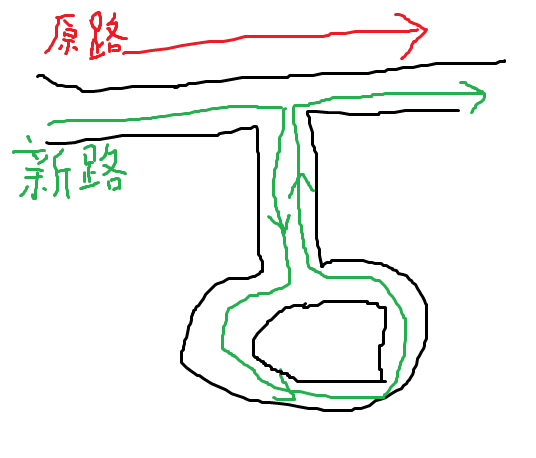
然后呢这个图画的有点丑了

我们发现，增广的路径就是环上的路径，往返的路径上两次xor就xor没了，对答案的贡献为0

然后所以我们枚举所有环，把这条环的xor扔进线性基，查询时候直接用1到n的一条路径去查询这个长度被线性基乱搞后的最大值

这题也就蓝题难度吧竟然是黑题

#include <bits/stdc++.h>
using namespace std;
struct edge
{
    int v;
    long long w;
    int ne;
}a[200010];
int n, m, tmp;
int h[50010];
long long dis[50010];
bool vis[50010];
long long linear_basis[70];
void add(int u, int v, long long w)
{
    a[++tmp] = (edge){v, w, h[u]};
    h[u] = tmp;
}
bool insert(long long x)
{
    for (int i = 63; i >= 0; i--)
    {
        if (x & (1LL << i))
        {
            if(linear_basis[i] == 0)
            {
                linear_basis[i] = x;
                return true;
            }
            x ^= linear_basis[i];
        }
    }
    return false;
}
long long query(long long x)
{
    for (int i = 63; i >= 0; i--)
        if ((x ^ linear_basis[i]) > x)
            x ^= linear_basis[i];
    return x;
}
void search(int x, long long y)
{
    dis[x] = y;
    vis[x] = 1;
    for (int i = h[x]; i != 0; i = a[i].ne)
        if (vis[a[i].v] == 0)
            search(a[i].v, y ^ a[i].w);
        else
            insert(y ^ a[i].w ^ dis[a[i].v]);
}
int main()
{
    scanf("%d%d", &n, &m);
    long long z;
    for (int x, y, i = 1; i <= m; i++)
    {
        scanf("%d%d%lld", &x, &y, &z);
        add(x, y, z);
        add(y, x, z);
    }
    search(1, 0);
    printf("%lld\n", query(dis[n]));
    return 0;
}