【例题收藏】◇例题·II◇ Berland and the Shortest Paths

◇例题·II◇ Berland and the Shortest Paths

题目来源：Codeforce 1005F +传送门+

---

◆ 简单题意

给定一个n个点、m条边的无向图。保证图是连通的，且m≥n-1。

以首都（1节点）为根节点生成最小树。树的值定义为每个节点的深度和（根节点深度0）。举个例子：

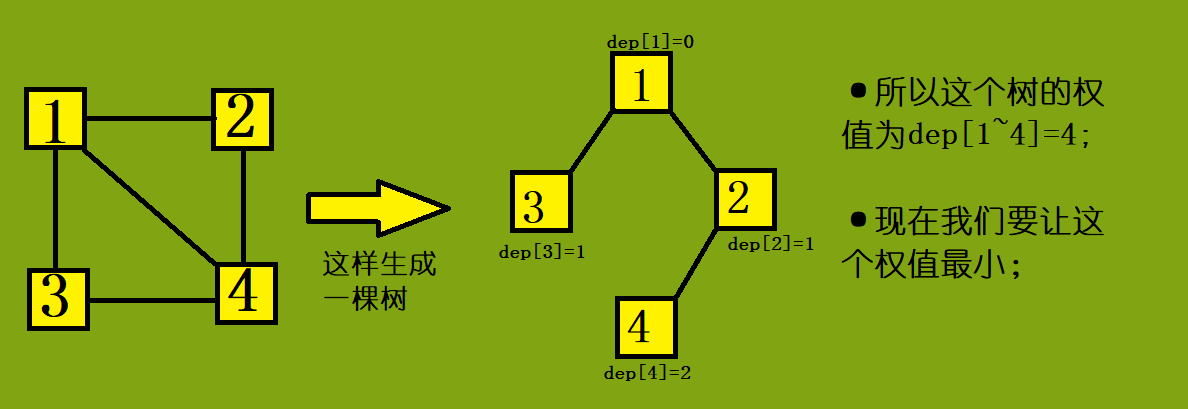
而我们知道，可能有多种情况使树的权值最小，题目给出了一个整数k，如果最小树的生成方案数为ans，当 ans≤k 时，将 ans 种方案全部输出；当 ans>k 时，任意输出 k 种不同生成方案即可。输出方案格式为一个01串，第i个字符如果为0，表示不选第i条边（按照输入顺序），1为选择第i条边。

---

◆ 解析

其实点 i 的深度 dep[i] 就是根节点1到 i 的路径，而我们知道 1 到 i 没有任何一条路径短于它们的最短路径，所以生成树的权值最小时，根节点到每个点的距离就是原图中根节点到每个节点的最短路径。也就是说，我们生成的最小树就是一个最短路径树。然而显然有时候存在多条最短路径，这也就造成了我们生成的最小树有多种解。于是我们假装生成一棵树，实际上只是生成一个图。

由于这道题的边权都是等价的（不如就把边权看成1吧），我们可以用BFS直接求得最短路，所以说其实这也是一个BFS序图。为了考虑每种情况，我们把所有最小的BFS序边连上。下面再举一个生成BFS序图的例子（希望入门reader可以理解）：

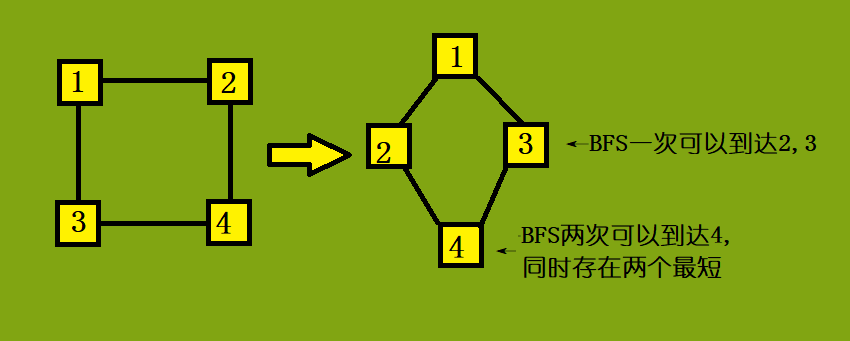
这样我们就生成了一个BFS序有根图，由于我们要生成树，而树的每一个节点的父节点少于一个。在上图中，4的父节点有两个，因此需要断开一条边——两条边是等价的，断掉任意一条即可。

我们可以把 u→v 的边存入v的边集 min_edg[v] ，那么最小权值树则是对于每一个除根节点之外的 v，选择 min_edg[v] 中的任意一条边，所以方案总数为 （除去根节点 i:2~n）min_edg[v]的边数之积。最后再DFS递归求方案即可（具体见代码）。

---

◆ 源代码

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 #include<queue>
 using namespace std;
 const int MAXN=int(2e5);
 const int INF=int(1e9);
 int n_pnt,n_edg,k;
 int dis[MAXN+];
 vector<pair<int,int> > lnk[MAXN+];
 vector<pair<int,int> > min_edg[MAXN+];
 void BFS(int start)
 {
     fill(dis,dis+MAXN+,INF);
     dis[start]=;
     queue<int> que;
     que.push(start);
     while(!que.empty())
     {
         int u=que.front();que.pop();
         for(int i=;i<lnk[u].size();i++)
         {
             int v=lnk[u][i].first,id=lnk[u][i].second,Stp=dis[u]+;
             if(Stp>dis[v]) continue;
             min_edg[v].push_back(make_pair(u,id));
             if(Stp!=dis[v])
                 dis[v]=Stp,que.push(v);
         }
     }
 }
 bool chose[MAXN+];int cnt;
 void DFS(int v)
 {
     if(v==n_pnt+)
     {
         cnt++;
         for(int i=;i<=n_edg;i++)
             printf("%d",chose[i]);
         printf("\n");
         return;
     }
     for(int i=;i<min_edg[v].size();i++)
     {
         chose[min_edg[v][i].second]=true;
         DFS(v+);
         chose[min_edg[v][i].second]=false;
         if(cnt==k) return;
     }
 }
 int main()
 {
     scanf("%d%d%d",&n_pnt,&n_edg,&k);
     for(int i=,u,v;i<n_edg;i++)
         scanf("%d%d",&u,&v),
         lnk[u].push_back(make_pair(v,i+)),
         lnk[v].push_back(make_pair(u,i+));
     BFS();
     long long ans=;
     for(int i=;i<=n_pnt;i++)
     {
         ans*=min_edg[i].size();
         if(ans>k) break;
     }
     printf("%lld\n",min(k*1ll,ans));
     DFS();
     return ;
 }

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~）