压缩感知重构算法之压缩采样匹配追踪(CoSaMP)





然后在网上找到了符合论文中符号的代码。
- function Sest = cosaomp(Phi,u,K,tol,maxiterations)
- Sest = zeros(size(Phi,2),1);
- v = u;
- t = 1;
- numericalprecision = 1e-12;
- T = [];
- while (t <= maxiterations) && (norm(v)/norm(u) > tol)
- y = abs(Phi'*v);
- [vals,z] = sort(y,'descend');
- Omega = find(y >= vals(2*K) & y > numericalprecision);
- T = union(Omega,T);
- b = pinv(Phi(:,T))*u;
- [vals,z] = sort(abs(b),'descend');
- Kgoodindices = (abs(b) >= vals(K) & abs(b) > numericalprecision);
- T = T(Kgoodindices);
- Sest = zeros(size(Phi,2),1);
- phit = Phi(:,T);
- b = pinv(phit)*u;
- Sest(T) = b;
- v = u - phit*b;
- t = t+1;
- end
接下来综合代码我准备强行解释一波论文算法的伪代码流程,哎呀半懂半懂希望以后要全懂全懂。


1、CoSaMP重构算法流程




步骤(5)稍微有点绕,综合代码理解一下还是不难的。
2、压缩采样匹配追踪(CoSaOMP)Matlab代码(CS_CoSaMP.m)
- function [ theta ] = CS_CoSaMP( y,A,K )
- %CS_CoSaOMP Summary of this function goes here
- %Created by jbb0523@@2015-04-29
- %Version: 1.1 modified by jbb0523 @2015-05-09
- % Detailed explanation goes here
- % y = Phi * x
- % x = Psi * theta
- % y = Phi*Psi * theta
- % 令 A = Phi*Psi, 则y=A*theta
- % K is the sparsity level
- % 现在已知y和A,求theta
- % Reference:Needell D,Tropp J A.CoSaMP:Iterative signal recovery from
- % incomplete and inaccurate samples[J].Applied and Computation Harmonic
- % Analysis,2009,26:301-321.
- [y_rows,y_columns] = size(y);
- if y_rows<y_columns
- y = y';%y should be a column vector
- end
- [M,N] = size(A);%传感矩阵A为M*N矩阵
- theta = zeros(N,1);%用来存储恢复的theta(列向量)
- Pos_theta = [];%用来迭代过程中存储A被选择的列序号
- r_n = y;%初始化残差(residual)为y
- for kk=1:K%最多迭代K次
- %(1) Identification
- product = A'*r_n;%传感矩阵A各列与残差的内积
- [val,pos]=sort(abs(product),'descend');
- Js = pos(1:2*K);%选出内积值最大的2K列
- %(2) Support Merger
- Is = union(Pos_theta,Js);%Pos_theta与Js并集
- %(3) Estimation
- %At的行数要大于列数,此为最小二乘的基础(列线性无关)
- if length(Is)<=M
- At = A(:,Is);%将A的这几列组成矩阵At
- else%At的列数大于行数,列必为线性相关的,At'*At将不可逆
- if kk == 1
- theta_ls = 0;
- end
- break;%跳出for循环
- end
- %y=At*theta,以下求theta的最小二乘解(Least Square)
- theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解
- %(4) Pruning
- [val,pos]=sort(abs(theta_ls),'descend');
- %(5) Sample Update
- Pos_theta = Is(pos(1:K));
- theta_ls = theta_ls(pos(1:K));
- %At(:,pos(1:K))*theta_ls是y在At(:,pos(1:K))列空间上的正交投影
- r_n = y - At(:,pos(1:K))*theta_ls;%更新残差
- if norm(r_n)<1e-6%Repeat the steps until r=0
- break;%跳出for循环
- end
- end
- theta(Pos_theta)=theta_ls;%恢复出的theta
- end
3、CoSaMP单次重构测试代码
- %压缩感知重构算法测试
- clear all;close all;clc;
- M = 64;%观测值个数
- N = 256;%信号x的长度
- K = 12;%信号x的稀疏度
- Index_K = randperm(N);
- x = zeros(N,1);
- x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的,且位置是随机的
- Psi = eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta
- Phi = randn(M,N);%测量矩阵为高斯矩阵
- A = Phi * Psi;%传感矩阵
- y = Phi * x;%得到观测向量y
- %% 恢复重构信号x
- tic
- theta = CS_CoSaMP( y,A,K );
- x_r = Psi * theta;% x=Psi * theta
- toc
- %% 绘图
- figure;
- plot(x_r,'k.-');%绘出x的恢复信号
- hold on;
- plot(x,'r');%绘出原信号x
- hold off;
- legend('Recovery','Original')
- fprintf('\n恢复残差:');
- norm(x_r-x)%恢复残差
运行结果如下:(信号为随机生成,所以每次结果均不一样)
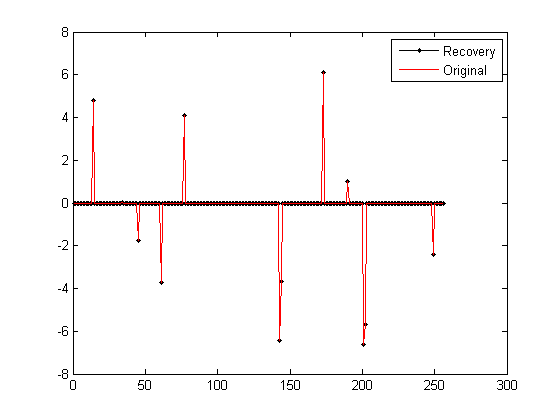
 2)Command windows
2)Command windows4、测量数M与重构成功概率关系曲线绘制例程代码
- clear all;close all;clc;
- %% 参数配置初始化
- CNT = 1000;%对于每组(K,M,N),重复迭代次数
- N = 256;%信号x的长度
- Psi = eye(N);%x本身是稀疏的,定义稀疏矩阵为单位阵x=Psi*theta
- K_set = [4,12,20,28,36];%信号x的稀疏度集合
- Percentage = zeros(length(K_set),N);%存储恢复成功概率
- %% 主循环,遍历每组(K,M,N)
- tic
- for kk = 1:length(K_set)
- K = K_set(kk);%本次稀疏度
- M_set = 2*K:5:N;%M没必要全部遍历,每隔5测试一个就可以了
- PercentageK = zeros(1,length(M_set));%存储此稀疏度K下不同M的恢复成功概率
- for mm = 1:length(M_set)
- M = M_set(mm);%本次观测值个数
- fprintf('K=%d,M=%d\n',K,M);
- P = 0;
- for cnt = 1:CNT %每个观测值个数均运行CNT次
- Index_K = randperm(N);
- x = zeros(N,1);
- x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的,且位置是随机的
- Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵
- A = Phi * Psi;%传感矩阵
- y = Phi * x;%得到观测向量y
- theta = CS_CoSaMP(y,A,K);%恢复重构信号theta
- x_r = Psi * theta;% x=Psi * theta
- if norm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功
- P = P + 1;
- end
- end
- PercentageK(mm) = P/CNT*100;%计算恢复概率
- end
- Percentage(kk,1:length(M_set)) = PercentageK;
- end
- toc
- save CoSaMPMtoPercentage1000 %运行一次不容易,把变量全部存储下来
- %% 绘图
- S = ['-ks';'-ko';'-kd';'-kv';'-k*'];
- figure;
- for kk = 1:length(K_set)
- K = K_set(kk);
- M_set = 2*K:5:N;
- L_Mset = length(M_set);
- plot(M_set,Percentage(kk,1:L_Mset),S(kk,:));%绘出x的恢复信号
- hold on;
- end
本程序运行结果:


压缩感知重构算法之压缩采样匹配追踪(CoSaMP)的更多相关文章
- [转]压缩感知重构算法之分段正交匹配追踪(StOMP)
分段正交匹配追踪(StagewiseOMP)或者翻译为逐步正交匹配追踪,它是OMP另一种改进算法,每次迭代可以选择多个原子.此算法的输入参数中没有信号稀疏度K,因此相比于ROMP及CoSaMP有独到的 ...
- 浅谈压缩感知(二十八):压缩感知重构算法之广义正交匹配追踪(gOMP)
主要内容: gOMP的算法流程 gOMP的MATLAB实现 一维信号的实验与结果 稀疏度K与重构成功概率关系的实验与结果 一.gOMP的算法流程 广义正交匹配追踪(Generalized OMP, g ...
- 浅谈压缩感知(二十五):压缩感知重构算法之分段正交匹配追踪(StOMP)
主要内容: StOMP的算法流程 StOMP的MATLAB实现 一维信号的实验与结果 门限参数Ts.测量数M与重构成功概率关系的实验与结果 一.StOMP的算法流程 分段正交匹配追踪(Stagewis ...
- 浅谈压缩感知(二十二):压缩感知重构算法之正则化正交匹配追踪(ROMP)
主要内容: ROMP的算法流程 ROMP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 一.ROMP的算法流程 正则化正交匹配追踪ROMP算法流程与OMP的最大不同之 ...
- 浅谈压缩感知(二十三):压缩感知重构算法之压缩采样匹配追踪(CoSaMP)
主要内容: CoSaMP的算法流程 CoSaMP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 一.CoSaMP的算法流程 压缩采样匹配追踪(CompressiveS ...
- 压缩感知重构算法之子空间追踪(SP)
SP的提出时间比CoSaMP提出时间稍晚一些,但和压缩采样匹配追踪(CoSaMP)的方法几乎是一样的.SP与CoSaMP主要区别在于“In each iteration, in the SP algo ...
- 浅谈压缩感知(二十四):压缩感知重构算法之子空间追踪(SP)
主要内容: SP的算法流程 SP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 SP与CoSaMP的性能比较 一.SP的算法流程 压缩采样匹配追踪(CoSaMP)与子 ...
- 浅谈压缩感知(二十六):压缩感知重构算法之分段弱正交匹配追踪(SWOMP)
主要内容: SWOMP的算法流程 SWOMP的MATLAB实现 一维信号的实验与结果 门限参数a.测量数M与重构成功概率关系的实验与结果 SWOMP与StOMP性能比较 一.SWOMP的算法流程 分段 ...
- 浅谈压缩感知(二十一):压缩感知重构算法之正交匹配追踪(OMP)
主要内容: OMP的算法流程 OMP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 稀疏度K与重构成功概率关系的实验与结果 一.OMP的算法流程 二.OMP的MATL ...
随机推荐
- OSGi-开发环境的建立和HelloWorld(04)
1 OSGi开发环境的建立 1.1 Equinox是什么 从代码角度来看,Equinox其实就是OSGi核心标准的完整实现,并且还在这个基础上增加了一些额外的功能(比如为框架增加了命令行和程序执行的入 ...
- 高德地图markers生成和点击
因为自己平时上班也是比较忙,遇到什么写什么,希望能给现在的你一些帮助,都是自己在工作中遇到的问题,给自己一个提醒,也是分享 相信很多人在做高德地图开发的时候,对于新手,官方的demo解读单个marke ...
- Markdown使用简单示例
标题示例: 标题一 #标题一 标题二 #标题二 标题三 ###标题三 标题四 ####标题四 标题五 #####标题五 标题六 ######标题六 连接示例 [](跳转 ...
- python 部署 Restful web
使用python web做Restful 风格,很简单,采用Flask框架轻松实现一个RESTful的服务. Restful相关介绍请查看:https://www.ibm.com/developerw ...
- oracle pl/sql 基础
一.pl/sql developer开发工具pl/sql developer是用于开发pl/sql块的集成开发环境(ide),它是一个独立的产品,而不是oracle的一个附带品. 二.pl/sql介绍 ...
- Apache Spark 2.2.0 中文文档 - Submitting Applications | ApacheCN
Submitting Applications 在 script in Spark的 bin 目录中的spark-submit 脚本用与在集群上启动应用程序.它可以通过一个统一的接口使用所有 Spar ...
- 策略模式Strategy
定义一系列的算法,把他们封装起来,使得算法独立于适用对象. 比如,一个系统有很多的排序算法,但是使用哪个排序算法是客户对象的自有.因此把每一个排序当做一个策略对象,客户调用哪个对象,就使用对应的策略方 ...
- Mybatis #{ } 和 ${ } 区别
动态 SQL 是 Mybatis 的强大特性之一,也是它优于其他 ORM 框架的一个重要原因.Mybatis 在对 sql 语句进行预编译之前,会对 sql 进行动态解析,解析为一个 BoundSql ...
- uvalive 3029 City Game
https://vjudge.net/problem/UVALive-3029 题意: 给出一个只含有F和R字母的矩阵,求出全部为F的面积最大的矩阵并且输出它的面积乘以3. 思路: 求面积最大的子矩阵 ...
- FPGA在电平接口领域的应用
电子技术的发展,产生了各种各样的电平接口. TTL电平: TTL电平信号之所以被广泛使用,原因是因为:通常我们采用二进制来表示数据.而且规定,+5V等价于逻辑"1",0V等价于逻辑 ...
