有向图和拓扑排序Java实现

package practice;

import java.util.ArrayDeque;
import java.util.Iterator;
import java.util.Stack;

public class TestMain {
    public static void main(String[] args) {
        Digraph a = new Digraph(13);
        a.addEdge(0, 1);a.addEdge(0, 5);/*a.addEdge(2, 3);*/a.addEdge(2, 0);a.addEdge(3, 2);
        /*a.addEdge(3, 5);*/a.addEdge(4, 3);/*a.addEdge(4, 2);*/a.addEdge(5, 4);a.addEdge(6, 0);
        a.addEdge(6, 4);a.addEdge(6, 9);a.addEdge(7, 6);/*a.addEdge(7, 8);*/a.addEdge(8, 7);
        a.addEdge(8, 9);a.addEdge(9, 10);a.addEdge(9, 11);a.addEdge(10, 12);a.addEdge(11, 4);
        a.addEdge(11, 12);/*a.addEdge(12, 9);*/

        System.out.println(a);

        DirectedDFS dfsa = new DirectedDFS(a);
        //第一种方法检查环
        System.out.println(dfsa.hasCycle());
        System.out.println();

        Digraph b = new Digraph(13);
        b.addEdge(0, 1);b.addEdge(0, 5);b.addEdge(2, 3);b.addEdge(2, 0);b.addEdge(3, 5);
        b.addEdge(5, 4);b.addEdge(6, 4);b.addEdge(6, 9);b.addEdge(7, 6);b.addEdge(8, 7);
        b.addEdge(9, 10);b.addEdge(9, 11);b.addEdge(9, 12);b.addEdge(11, 12);b.addEdge(0, 6);

        DirectedDFS dfsb = new DirectedDFS(b);
        //第一种方法检查环
        System.out.println(dfsb.hasCycle());
        for (Integer integer : dfsb.Topological()) {
            System.out.print(integer + " ");
        }
    }
}

/*
 * 有向图处理
 */
class DirectedDFS {
    private boolean[] marked;
    private Digraph G;
    private Stack<Integer> cycle;
    private int []edgeTo; //轨迹
    private boolean[] onStack; //当前搜索轨迹
    private Stack<Integer> reversePost; //所有顶点的逆后续排列
    /*
     * 在图处理类里初始化图
     */
    public DirectedDFS(Digraph G) {
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];
        this.G = G;
        DirectedCycle(); //检测环
        DepthFirstOrder(); //拓扑排序
    }

    /*
     * 深度优先搜索
     */
    private void dfs(int s) {
        marked[s] = true;
        for (int w : G.adj(s)) {
            if (!marked[w]) {
                edgeTo[w] = s;
                dfs(w);
            }
        }
    }
    /*
     * 广度优先搜索
     */
    private void bfs(int s) {
        ArrayDeque<Integer> deque = new ArrayDeque<Integer>();
        deque.add(s);
        marked[s] = true;
        int c;
        while (!deque.isEmpty()) {
            c = deque.poll();
            for (int w : G.adj(c)) {
                if (!marked[w]) {
                    marked[w] = true;
                    edgeTo[w] = c;
                    deque.add(w);
                }
            }
        }
    }

    /*
     * 在G中找到s所有可达的顶点(可以用marked()检测)
     */
    public void DFS(int s) {
        dfs(s);
    }
    /*
     * 在G中找到source中的所有顶点可到达的所有顶点
     */
    public void DFS(Iterable<Integer> sources) {
        for (Integer integer : sources) {
            dfs(integer);
        }
    }
    /*
     * v是可达的吗
     */
    public boolean marked(int v) {
        return marked[v];
    }

    /*
     * 检测s到c的的路径
     */
    public void DFDPath(int s, int c) {
        for (int i = 0; i < marked.length; i++) {
            marked[i] = false;
        }
        dfs(s);
        System.out.print(c + "<-");
        while (edgeTo[c] != s) {
            c = edgeTo[c];
            System.out.print(c + "<-");
        }
        c = edgeTo[c];
        System.out.println(c);
    }

    /*
     * 检测s到c的的路径(最短)
     */
    public void BFDPath(int s, int c) {
        for (int i = 0; i < marked.length; i++) {
            marked[i] = false;
        }
        bfs(s);
        System.out.print(c + "<-");
        while (edgeTo[c] != s) {
            c = edgeTo[c];
            System.out.print(c + "<-");
        }
        c = edgeTo[c];
        System.out.println(c);
    }

    /*
     * 检测该有向图是否有环
     * 要标记当前路径,检查 将要检查到的(并已被标记过的点)是否在当前路径
     */

    private void DirectedCycle() {
        onStack = new boolean[G.V()];
        //先将标记归零
        for (int i = 0; i < marked.length; i++) {
            marked[i] = false;
        }
        //挨个搜索节点,标记过的节点就不搜了
        for (int i = 0; i < G.V(); i++) {
            if (!marked[i]) DirectedCycleDfs(i);
        }
    } 

    private void DirectedCycleDfs(int s) {
        onStack[s] = true; //onStack[v] = true 说明将v加入当前路径
        marked[s] = true;
        for (int w : G.adj(s)) {
            if (this.hasCycle()) return;
            else if (!marked[w]) {
                edgeTo[w] = s;
                DirectedCycleDfs(w);
            }
            else if (onStack[w]) {
                //将这条路径保存到cycle
                cycle = new Stack<Integer>();
                for (int x = s; x != w; x = edgeTo[x])
                    cycle.push(x);

                cycle.push(w);
                cycle.push(s);
            }
        }
        onStack[s] = false; //将要切换到另一条路径,将v从当前路径剔除
    }
    //有环返回true无环返回false
    public boolean hasCycle() { return cycle != null;}
    //返回找到的环
    public Iterable<Integer> cycle() { return cycle;}

    /*
     * 排出顶点的深度优先次序的深度优先搜索
     * 拓扑排序 即被指向的一定在指向的后面
     */
    public void DepthFirstOrder() {
        reversePost = new Stack<Integer>();
        for (int i = 0; i < marked.length; i++) {
            marked[i] = false;
        }
        for (int i = 0; i < G.V(); i++) {
            if (!marked[i]) dfo(i);
        }
    }
    private void dfo(int s) {
        marked[s] = true;
        for (int w : G.adj(s)) {
            if (!marked[w]) {
                dfo(w);
            }
        }
        reversePost.push(s); //可以保证被指向的肯定比指向的先进入栈,所以可以拓扑排序
    }
    /*
     * 拓扑排序
     */
    public Iterable<Integer> Topological() {
        if (hasCycle()) { return null;} //有环则不能拓扑排序
        return reversePost;
    }
}

/*
 * 有向图
 */
class Digraph {
    private Bag<Integer>[] digraph;
    private int V; //点数
    private int E; //边数
    public Digraph(int V) {
        this.V = V;
        digraph = (Bag<Integer>[]) new Bag[V];
        for (int i = 0; i < V; i++) {
            digraph[i] = new Bag<Integer>();
        }
    }

    public int V() { return V;}
    public int E() { return E;}

    public void addEdge(int v, int w) {
        digraph[v].add(w);
        E++;
    }

    public Iterable<Integer> adj(int V) {
        return digraph[V];
    }

    public Digraph reverse() {
        Digraph result = new Digraph(V);
        for (int i = 0; i < V; i++) {
            for (Integer integer : digraph[i]) {
                result.addEdge(i, integer);
            }
        }
        return result;
    }

    public String toString() {
        String s = V + " vertices, " + E + " edges\n";
        for (int v = 0; v < V; v++) {
            s += v + ": ";
            for (Integer integer : this.adj(v)) {
                s += integer + " ";
            }
            s += "\n";
        }
        return s;
    }
}

/*
 * 背包
 */
class Bag<T> implements Iterable<T> {
    Node first;

    private class Node {
        T value;
        Node next;
    }

    public void add(T value) {
        Node oldfirst = first;
        first = new Node();
        first.value = value;
        first.next = oldfirst;
    }

    @Override
    public Iterator<T> iterator() {
        return new BagIterator();
    }

    private class BagIterator implements Iterator<T> {
        Node node = first;

        @Override
        public boolean hasNext() {
            return node != null;
        }

        @Override
        public T next() {
            T tempt = node.value;
            node = node.next;
            return tempt;
        }
    }
}

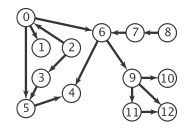
上面用到的有向图（Digraph b）