UVA 1394 And Then There Was One / Gym 101415A And Then There Was One / UVAlive 3882 And Then There Was One / POJ 3517 And Then There Was One / Aizu 1275 And Then There Was One （动态规划，思维题）

Description

Let’s play a stone removing game.

Initially, n stones are arranged on a circle and numbered 1, …, n clockwise (Figure 1). You are also given two numbers k and m. From this state, remove stones one by one following the rules explained below, until only one remains. In step 1, remove stone m. In step 2, locate the k-th next stone clockwise from m and remove it. In subsequent steps, start from the slot of the stone removed in the last step, make k hops clockwise on the remaining stones and remove the one you reach. In other words, skip (k − 1) remaining stones clockwise and remove the next one. Repeat this until only one stone is left and answer its number. For example, the answer for the case n = 8, k = 5, m = 3 is 1, as shown in Figure 1.

Initial state: Eight stones are arranged on a circle.

Step 1: Stone 3 is removed since m = 3.

Step 2: You start from the slot that was occupied by stone 3. You skip four stones 4, 5, 6 and 7 (since k = 5), and remove the next one, which is 8.

Step 3: You skip stones 1, 2, 4 and 5, and thus remove 6. Note that you only count stones that are still on the circle and ignore those already removed. Stone 3 is ignored in this case.

Steps 4–7: You continue until only one stone is left. Notice that in later steps when only a few stones remain, the same stone may be skipped multiple times. For example, stones 1 and 4 are skipped twice in step 7.

Final State: Finally, only one stone, 1, is on the circle. This is the final state, so the answer is 1.

Input

The input consists of multiple datasets each of which is formatted as follows.

n k m

The last dataset is followed by a line containing three zeros. Numbers in a line are separated by a single space. A dataset satisfies the following conditions.

2 ≤ n ≤ 10000, 1 ≤ k ≤ 10000, 1 ≤ m ≤ n

The number of datasets is less than 100.

Output

For each dataset, output a line containing the stone number left in the final state. No extra characters such as spaces should appear in the output.

Sample Input

8 5 3

100 9999 98

10000 10000 10000

0 0 0

Sample Output

1

93

2019

Http

UVA:https://vjudge.net/problem/UVA-1394

Gym:https://vjudge.net/problem/Gym-101415A

UVAlive:https://vjudge.net/problem/UVALive-3882

POJ:https://vjudge.net/problem/POJ-3517

Aizu:https://vjudge.net/problem/Aizu-1275

Source

动态规划，思维

题目大意

约瑟夫问题的变式。先指定第m个人必须死，然后每隔k个人死一个。求最后那个死的人的编号是什么。

解决思路

首先不考虑第一个必须死的人是m的情况。我们把n个人编号为[0,n-1]。那么第一轮出局的就是编号为k-1的人，剩下的人的编号是\([0,k-2]\cup[k,n-1]\)。

然后我们从编号为k的人开始，循环一圈给所有人重新分配编号

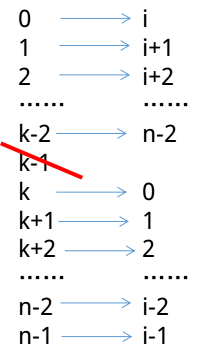
然后我们就可以发现原来n个人的题目就变成了n-1的规模。运用这种方法，我们就可以推到n=1的情况，而此时，F[1]=0。

那么，既然现在知道n=1的结果，那么我们考虑从1开始正着推出n。我们设F[i]表示i个人中最后存活的人的编号。现在我们知道F[i-1]，怎么推出F[i]呢？

其实这个问题就是问如何用存活者在i-1个人中的编号求出存活者在i个人中的编号。我们知道，从原问题推到子问题其实是把所有人的编号-k，那么从子问题推到原问题就是把人的编号+k，但要注意，此时+k可能会大于当前人的规模i，所以要对i取膜。

综上，动态转移的方程就是

\[F[i]=(F[i-1]+k)\%i
\]

当然这个式子还可以化简。因为F[i]的状态只与F[i-1]有关，所以我们可以直接用一个变量f代替整个F数组

\[f=(f+k)\%i
\]

最后再来考虑第一个死的人必须是m的情况，而我们第一个人是k，所以相当于我们要补上m-k的一个差量，所以最后的答案是f+m-k。另外需要注意的是，因为我们在递推的时候为了方便从0开始编号的，所以还要加上1，也就是f+m-k+1，再对n取膜。同时，如果取膜后结果是0或负数，要加上n变成正数。

代码不长，但要想到很难。

代码

#include<iostream>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<algorithm>

using namespace std;

const int inf=2147483647;

int main()

{

	int n,k,m;

	while (scanf("%d%d%d",&n,&k,&m)!=EOF)

	{

		if ((n==0)&&(m==0)&&(k==0))

			break;

		int f=0;//初始值

		for (int i=2;i<=n;i++)//动态转移

			f=(f+k)%i;

		f=(f+m-k+1)%n;//把开始是m的情况考虑进去

		if (f<=0)//取膜后有可能变成负数或0，此时要将其变成正数

			f=f+n;

		printf("%d\n",f);

	}

	return 0;

}