[solution] JZOJ-5458 质数

[solution] JZOJ-5458 质数

题面

Description

小X 是一位热爱数学的男孩子，在茫茫的数字中，他对质数更有一种独特的情感。小X 认为，质数是一切自然数起源的地方。

在小X 的认知里，质数是除了本身和1 以外，没有其他因数的数字。

但由于小X 对质数的热爱超乎寻常，所以小X 同样喜欢那些虽然不是质数，但却是由两个质数相乘得来的数。

于是，我们定义，一个数是小X 喜欢的数，当且仅当其是一个质数，或是两个质数的乘积。

而现在，小X 想要知道，在L 到R 之间，有多少数是他喜欢的数呢？

Input

第一行输入一个正整数Q，表示询问的组数。

接下来$Q$ 行。包含两个正整数L 和R。保证L≤R。

Output

输出Q 行，每行一个整数，表示小X 喜欢的数的个数。

Sample Input

输入1：
1
1 6
输入2：
10
282 491
31 178
645 856
227 367
267 487
474 697
219 468
582 792
315 612
249 307
输入3：
10
20513 96703
15236 86198
23185 78205
40687 48854
42390 95450
63915 76000
36793 92543
35347 53901
44188 76922
82177 90900

Sample Output

输出1：
5
样例1解释：
6以内的质数有2,3,5，而4=2*2,6=2*3。因此2,3,4,5,6都是小X 喜欢的数，而1 不是。
输出2：
97
78
92
65
102
98
114
90
133
29
输出3：
24413
23001
17784
2669
16785
3833
17712
6028
10442
2734

Data Constraint

---

---

---

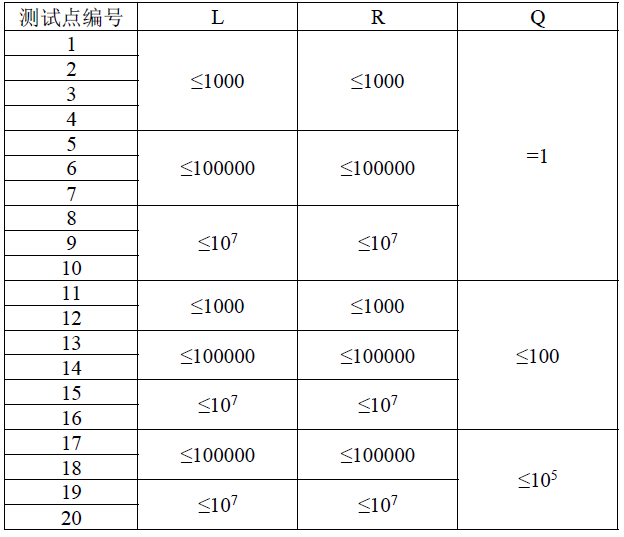
分割线

---

---

---

是不是很简单？？似曾相识的赶脚？？是不是一下子切掉了？？

对的这就是一个很水的题目，本蒟蒻的给出了一个暴力的做法：

就像以下这样

Step1：暴力筛出1-10000000里的所有质数

Step2：暴力筛出1-10000000里的由2个质数相乘得到的数

Step3：对筛出来的数赋值为1，其他为0，暴力搞前缀和

Step4：O(1)时间回答询问即可

对就是这么暴力，预处理消耗633ms，回答100000次询问总共才消耗大约70ms

暴力解法的代码见下（捂脸）

Code

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#define ll long long
#define lb(x) (x&-x)
using namespace std;
ll p[10000005];
ll q[10000005];
ll c[10000005];
void up(ll x,ll num){for(ll i=x;i<=10000000;i+=lb(i)) c[i]+=num;}
ll gs(ll x){ll ans=0;for(ll i=x;i;i-=lb(i)) ans+=c[i];return ans;}
ll ask(ll l,ll r){return gs(r)-gs(l-1);}
int main(){
	freopen("prime.in","r",stdin);
	freopen("prime.out","w",stdout);
	memset(p,0,sizeof(p));
	memset(q,0,sizeof(q));
	ll tot=0;
	for(ll i=2;i<=10000000;i++){
		if(!p[i]){
			q[tot]=i;up(i,1);
			for(ll j=0;j<=tot;j++){
				ll ppp=q[j]*q[tot];
				if(ppp<=10000000)
					up(ppp,1);
				else
					break;
			}
			tot++;
			for(ll j=2;i*j<=10000000;j++){
				p[i*j]=1;
			}
		}
	}ll cnt=0;
	ll q;
	scanf("%lld",&q);
	while(q--){
		ll a,b;
		if(a<1) a=1;
		if(b>10000000) b=10000000;
		scanf("%lld %lld",&a,&b);
		printf("%lld\n",ask(a,b));
	}return 0;
}